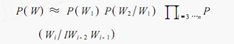文分词介绍

中文分词相较于英文分词要难许多，因为英文本身就是由单词与空格组成的，而中文则是由独立的字组成的，但同时语义却是有词来表达的。因此对于中文的分析与研究，首先应寻找合适的方法进行分词。现有的中文分词技术主要分为规则分词，统计分词与规则加统计相结合的方式，接下来将分别介绍。

规则分词

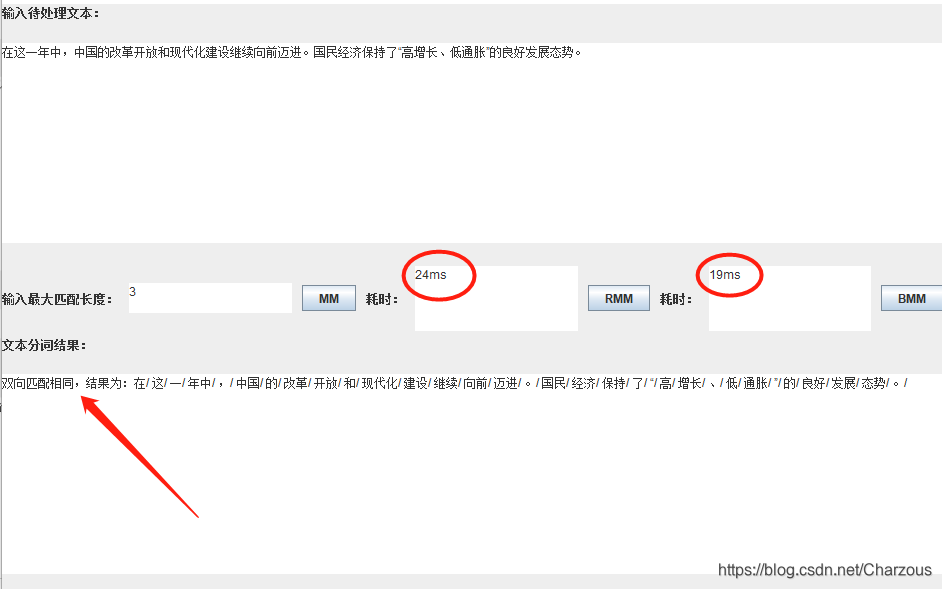
规则分词主要是通过构建词典，对需要进行分词的语句与词典中的词语进行匹配，从而实现切分，具体主要有正向最大匹配法，逆向最大匹配法，双向最大匹配法。

正向最大匹配法

正向最大匹配法实现的原理如下：假设分词词典中最长词语的长度为 i， 那么则选取需要进行分词的语句中的前 i个字，查询是否匹配词典中长度为i的词。如果匹配，则进行切分；如果不匹配，则选取i-1个字查询分词词典是否匹配，以此类推，直至成功切分。接着对于剩余的字段采取同样的方法进行切分，直到最后完全切分。

比如我们现在要对“正向最大匹配法”进行分词，而我们的分词字典最长的词语长度为4。首先选取前四个字“正向最大”，词典中并无匹配，那么接着选取前三个字“正向最”，依旧没有，再选择前两个字“正向”，成功匹配，则进行切分，接着选取之后的四个字“最大匹配”，以此类推，继续切分，直至切分完毕。

逆向最大匹配法

逆向最大匹配法的原理与正向是基本一致的，只是逆向最大匹配法是从句尾开始进行匹配。由于汉语中偏正结构较多，一般逆向最大匹配法的结果准确度要稍高于正向最大匹配法

双向最大匹配法

双向最大匹配法是在正向与逆向最大匹配法的基础上对两者结果进行比较，选取切分词数较少的一个结果作为最终分词。双向最大匹配法在实际中运用更为广

接下来，我们可以通过python实现简单的三种最大匹配法：

#读取训练字典
def readDict(path):dictionary=[]maximum=0with open(path,'r',encoding='utf-8') as f:for line in f:line=line.strip()if line:dictionary.append(line)if maximum<len(line):maximum=len(line)else:continue           return dictionary,maximum#正向最大匹配法
def forwardCut(text,dictionary,maximum):result=[]index=0while index<len(text):word=Nonefor i in range(maximum,0,-1):if len(text)-index<i+1:continuepiece=text[index:index+i]if piece in dictionary:word=pieceresult.append(word)index+=ibreakif word ==None:result.append(text[index:index+1])index+=1return result#逆向最大匹配法
def backwardCut(text,dictionary,maximum):result=[]index=len(text)while index>0:word=Nonefor i in range(maximum,0,-1):if index-i<0:continuepiece=text[index-i:index]if piece in dictionary:word=pieceresult.append(word)index-=ibreakif word==None:result.append(text[index-1:index])index-=1return result[::-1]#双向最大匹配法
def compare(text,dictionary,maximum):Fresult=forwardCut(text,dictionary,maximum)Bresult=backwardCut(text,dictionary,maximum)if len(Fresult)<len(Bresult):return '/'.join(Fresult)else:return '/'.join(Bresult)

接下来，我们通过输入自制词典来比较三种分词方法的结果。词典如下：

正向最大匹配法：

dictionary,maximum=readDict('dic.utf8')
print('/'.join(forwardCut('双向最大匹配法',dictionary,maximum)))

输出结果为：

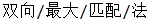
逆向最大匹配法：

print('/'.join(backwardCut('双向最大匹配法',dictionary,maximum)))

输出结果为：

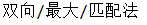
双向最大匹配法：

print(compare('双向最大匹配法',dictionary,maximum))

输出结果为：

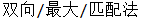
规则分词在一般的分词任务中已经能够得到较好的结果了，但是其缺点是需要大量人力物力去维护与更新分词词典。同时，对于新词，规则分词很难能够正确切割。相反，统计分词法较好的解决的这个问题。

统计分词

统计分词的基本思想是基于统计的概念，如果相连的字在不同的地方出现的次数越多，则其越有可能为一个词。因此我们可以利用出项概率来推测成词的可能性，从而实现分词。常见的统计分词方法有隐含马尔可夫（HMM）、条件随机场（CRF）等。接下来我们首先建立统计分词的语言模型，接着简单介绍一下HMM

统计分词语言模型

假设字符串的长度为m，那么对于这个字符串的概率分布可以描述为：
$$P(w_1,w_2,...,w_m)$$
通过链式法则，我们可以计算其概率值：
$$P(w_1,w_2,...,w_m)=P(w_1)P(w_2|w_1)P(w_3|w_2,w_1)\cdot \cdot \cdot P(w_i|w_{i-1},w_{i-2},..,w_1)\cdot \cdot \cdot P(w_m|w_{m-1}...w_1)$$
由于实际计算中，上式非常复杂，一般采用n-gram模型进行简化计算。n-gram模型即只考虑与字距离在n以内的文本对于这个字的影响。这样条件概率$P(w_i|w_{i-1},w_{i-2},..,w_1)$可以表示为：
$$P(w_i|w_{i-1},w_{i-2},..,w_1)=P(w_i|w_{i-1},w_{i-2},..,w_{i-(n-1)})$$
这样，当n=1时，为unigram模型：
$$P(w_i|w_{i-1},w_{i-2},..,w_1)=P(w_i)P(w_{i-1})\cdot \cdot \cdot P(w_1)$$
即为每个字单独的概率，但是unigram模型无法保留相邻字之间的关系，所以用于分词效果很不理想。当n=2,3时，模型可以保留一定的字之间的信息，又不至于使得计算过为复杂。

HMM模型

HMM即隐含马尔可夫模型，其基本思想为，将字在构造词的过程中所承担的角色归为4类：B(begin),M(middle),E(end),S(single)，接着，句子的分词任务便可以转化成对对句子中每个字进行标注角色的任务。在介绍HMM分词之前，首先需要介绍隐含马尔可夫过程。

隐含马尔可夫过程

一般来说，马尔可夫假设为：对于某一个随机过程，假设其存在n个状态S，那么对于某个特定的状态$S_i$，其概率分布只与前一个状态$S_{i-1}$有关。即：
$$P(S_i|S_1,S_2,...S_{i-1})=P(S_i|S_{i-1})$$
而符合马尔可夫假设的过程即为马尔可夫过程，也叫做马尔可夫链,一般的马尔可夫链表示如下：

上图中，每个圆代表一个状态，而线代表状态的转移与其概率。
而隐含马尔可夫过程是马尔可夫过程的扩展。在隐含马尔可夫过程中，不同时刻的状态$S_i$是不可见的，所以无法通过观测$S_i$来推测不同状态的概率分布。但是其在每个状态时会输出一个特定的特征${\sigma }_i$,并且这个特征${\sigma }_i$的概率分布与且仅与当前的状态有关。这就是隐含马尔可夫过程：

上图中，x代表状态，y代表对应特征。

HMM分词

了解了隐含马尔可夫过程，便可以介绍HMM分词模型了。通过上述内容我们可以很容易的发现HMM分词是典型的隐含马尔可夫过程。其中B\M\E\S代表不同的状态，而句子中每个字则代表其不同状态所产生的特征。而我们的任务则是根据概率分布推测句子中每一个字背后的状态，从而达到分词。
通过数学模型推导过程如下：
假设用$\lambda ={\lambda }_1{\lambda }_2...{\lambda }_n$表示句子与其中每一个字。而用$\sigma ={\sigma }_1{\sigma }_2...{\sigma }_n$表示对应的状态。则分词任务可以描述成：
$$maxP=maxP(\sigma |\lambda )=P({\sigma }_1{\sigma }_2...{\sigma }_n|{\lambda }_1{\lambda }_2...{\lambda }_n)$$
通过贝叶斯公式可以得到：
$$P(\sigma |\lambda )=\frac{P(\lambda |\sigma )P(\sigma )}{P(\lambda )}$$
对于$P(\lambda )$，其只与分词时使用的训练集有关，是个常数。则我们的模型可以转化为求：
$$maxP(\lambda |\sigma )P(\sigma )$$
根据隐含马尔可夫过程的假设
$$P(\lambda |\sigma )=P({\lambda }_1|{\sigma }_1)P({\lambda }_2|{\sigma }_2)\cdot \cdot \cdot P({\lambda }_n|{\sigma }_n)$$
同时，对于$P(\sigma )$:
$$P(\sigma )=P({\sigma }_1)P({\sigma }_2|{\sigma }_1)\cdot \cdot \cdot P({\sigma }_n|{\sigma }_1,{\sigma }_2...{\sigma }_{n-1})$$
根据马尔可夫过程的假设，当前状态只与上一状态有关：
$$P(\sigma )=P({\sigma }_1)P({\sigma }_2|{\sigma }_1)P({\sigma }_3|{\sigma }_2)\cdot \cdot \cdot P({\sigma }_n|{\sigma }_{n-1})$$
那么，$P(\sigma |\lambda )P(\sigma )$可以转化为：
$$P({\sigma }_1)P({\lambda }_1|{\sigma }_1)P({\sigma }_2|{\sigma }_1)P({\lambda }_2|{\sigma }_2)...P({\sigma }_n|{\sigma }_{n-1})P({\lambda }_n|{\sigma }_n)$$
其中，$P({\lambda }_i|{\sigma }_i)$称为发射概率，而$P({\sigma }_{i-1}|{\sigma }_i)$称为转移概率。通过具体设部分转移概率，可以排除部分不合理的转移概率，例如EB等。

veterbi算法

在实际中，一般运用veterbi算法求解HMM模型。veterbi算法一种动态规划算法，其在语音识别，机器翻译等领域应用及其广泛。其核心的思想是：如果最终的最优路径经过某个${\sigma }_i$，那么从初始节点到${\sigma }_{i-1}$也应该是最优路径。因为每一节点只会影响前后两个节点选择，那么假设最短路径不经过最优的子路径，那么用最优子路经代替现有路径，将生成更优路径，便与之前的自相矛盾了。
这样，我们在考虑每一个${\sigma }_i$时，只需要求出经过每一个${\sigma }_{i-1}$的最优路径，再考虑从每个${\sigma }_{i-1}$到每个${\sigma }_i$的最优路径。这样假设每步最多有$l$个状态，那么每步的计算量不超过$l^2$。计算效率为$o(n\cdot l^2)$,n为节点个数。
现在考虑分词问题，假设有一n个字符的字符串，那么分词任务为为每一字符贴上概率最大的状态标签（B/M/E/S）。转换成算法描述，即有n个节点，每个节点有四种可能的状态$\sigma$。这样，根据之前的语言模型描述，节点i-1到节点i的概率即为其发射概率乘转移概率$P({\sigma }_i|{\sigma }_{i-1})P({\lambda }_i|{\sigma }_i)$，根据veterbi算法，将最大概率描述为最短路径，在计算节点i时，我们已经求得到节点i-1四个状态的最短子路径，那么我们只需要分别计算节点i四个状态与之前求得的4条最短子路径相结合的最短路径便得到了到节点i的四条最短子路径。最终，我们将得到4条最终通过节点n四个状态的最优路径，通过比较路径长短便可以得到最终路径。这样，根据训练集所得的发射概率与转移概率，我们便可以求模型的最短路径，从而实现分词。

HMM在现如今的分词领域运用非常广泛，但它也有一定的缺点，过多的假设导致了与实际情况的偏离。但是在真实的语料中，更多的序列是多重的交互特征形式，部分序列存在长程相关性。
此外，条件随机场（CRF）与deep learning的发展拓宽了中文分词的技术，基于机器学习与神经网络的分词方法也逐渐得到实践。

[1]涂铭，刘祥，刘树春. Python自然语言处理实战：核心技术与算法. 北京. 机械工业出版社，2018.4