前言

我们常用的线性表是顺序存储结构和链式存储结构表示，是最基本、最简单、也是最常用的一种数据结构；一个线性表是由n个相同特性的数据的有限序列；比如java中的数组，链表；所以学习这两种结构表示是非常必要的。

线性表结构特点

均匀性数据元素是不同的，对于同一线性结构的各种数据元素必定有相同的数据类型和长度
有序性各数据元素在线性表中的位置只取决于它们的序号，数据元素之前的相对位置是线性的，即存在唯一的“第一个“和“最后一个”的数据元素，除了第一个和最后一个外，其它元素前面均只有一个数据元素(直接前驱)和后面均只有一个数据元素（直接后继）。

顺序存储结构

定义

用一组地址连续的存储单元依次存储线性表的结构，它以“物理位置相邻”来表示线性表中数据元素间的逻辑关系，可随机存取表中任一元素。

a1是a2的前驱，ai+1是ai的后继，a1没有前驱，an没有后继，n为线性表的长度，若n==0时，则线性表为空，这个长度n也就是我们平常size的概念，每个线性表，一定会有size的概念‘
这里还有个注意点，比如arraylist中实现，不要只局限于基本数据类型，可以存object类型的，这下面的

class ArrayList{
Student[40];
int size;
}

比如上图的结构也是顺序结构

插入与删除

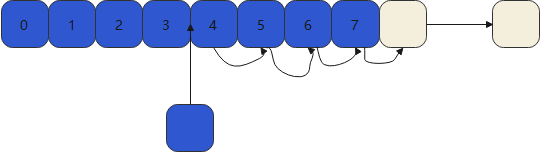
插入某个元素，一定是会将后面数据进行移动复制，就像 arraylist中下面进行插入

     System.arraycopy(elementData, index, elementData, index + 1,size - index);

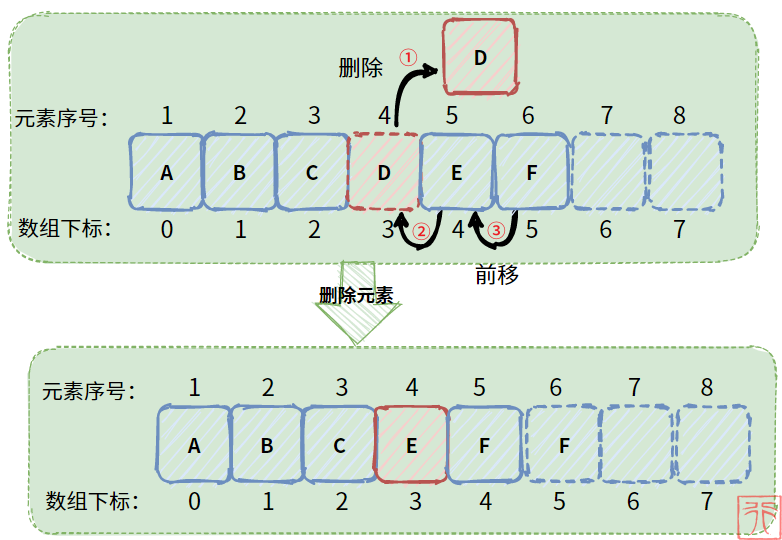
删除某个元素，也是需要将后面元素进行复制

优缺点

优点：
尾插效率高，支持随机访问。
缺点：
中间插入或者删除效率低。
应用：
数组
ArrayList

利用顺序结构的蛮力排序（蛮力法）

针对数据量少的排序方式，速度快；但数据量大了过后，时间会降低；

蛮力法（brute force method，也称为穷举法或枚举法）
是一种简单直接地解决问题的方法，
常常直接基于问题的描述，
所以，蛮力法也是最容易应用的方法。
但是，用蛮力法设计的算法时间特性往往也是最低的，
典型的指数时间算法一般都是通过蛮力搜索而得到的。（即输入资料的数量依线性成长，所花的时间将会以指数成长）

这种算法，在数据量很少的情况下，速度是最快的；也就是我们常说的冒泡法和快速排序法；

应用：数据量足够小，比如斗牛游戏的牌面排序；也就是 n一般小于5的情况

冒泡排序算法

第一轮进行只要当前点大于（或者小于）下个结点，就进行交换，就能取到一个最大（最小）的结点，这样不断循环

实现代码

 for(int i=array.length-1;i>0;i--) {boolean flag=true;for (int j = 0; j < i; j++) {if (array[j] > array[j + 1]) {int temp = array[j];array[j] = array[j + 1];array[j + 1] = temp;flag=false;}}if(flag){break;}}

上面的代码分为第一轮，首先冒泡到 array.length-1

 for(int i=array.length-1;i>0;i--) {

第二轮需要在剩余的不断交换

 for (int j = 0; j < i; j++) {

这样的时间复杂度的就是 n(n-1)/2 , 具体就是 n ,n-1,n-2.....1 相加
针对小数据量，做了个flag进行优化，数据已经排列好时，就先退出不走后面逻辑

这里做的一个花色和点数进行比较排序数据利用对象进行排序

首先做一个 cards 需要排序的方式利用comparable ;

public class Cards implements Comparable{public int pokerColors;//花色public int cardPoints;//点数public Cards(int pokerColors, int cardPoints) {this.pokerColors = pokerColors;this.cardPoints = cardPoints;}//提供一个方法，用来比较对象的大小@Overridepublic int compareTo(@NonNull Object o) {Cards c=(Cards)o;if(this.cardPoints>c.cardPoints){return 1;}else if(this.cardPoints<c.cardPoints){return -1;}if(this.pokerColors>c.pokerColors){return 1;}else if(this.pokerColors<c.pokerColors){return -1;}return 0;}@Overridepublic String toString() {return "Cards{" +"pokerColors=" + pokerColors +", cardPoints=" + cardPoints +'}';}}

进行冒泡排序数据

  for(int i=array.length-1;i>0;i--) {boolean flag=true;for (int j = 0; j < i; j++) {if (array[j].compareTo(array[j+1])>0) {Cards temp = array[j];array[j] = array[j + 1];array[j + 1] = temp;flag=false;}}if(flag){break;}}

冒泡法应用场景，在数据很多已经排序完成，则使用冒泡效率是非常高的

选择排序算法

该算法是快排的基础，理解快排，一定要理解选择排序；

第一轮进行选择一个基准结点一般为0结点，遍历数组，一旦遇到比他小（大）进行指针下标交换，第一轮下来，就能找到最小的点的指针，然后与基准点进行交换，基准点就能找到最小的数据

具体的代码

    public static void selectSort(int[] array){for(int i=0;i<array.length-1;i++) {int index = i;for (int j = i+1; j < array.length; j++) {if (array[j] < array[index]) {index = j;}}//{1,2,5,8,3,9,4,6,7};if(index!=i) {//如果已经是最小的，就不需要交换int temp = array[index];array[index] = array[i];array[i] = temp;}}}

针对蛮力法的应用，一般是小于5的数据可以使用，如果数据量大，不使用该种算法

链表式存储结构

线性表下定义链式存储结构

种类

单链表

单链表中基本单位为节点，而每个节点分为数据域和指针域；而指针域指向的是下个节点的下标；数据域则可以代表很多东西包括数据，还有其他属性

针对插入和删除节点的情况

这就是单向链表的删除和添加节点的过程

单链表的应用（链式奇数排序对麻将进行排序）

解决思路

创建对应的麻将对象

public class Mahjong {public int suit;//筒，万，索public int rank;//点数 一  二  三public Mahjong(int suit, int rank) {this.suit = suit;this.rank = rank;}@Overridepublic String toString() {return "("+this.suit+" "+this.rank+")";}
}

需要分别按花色和大小进行排序

      //先对点数进行分组LinkedList[] rankList=new LinkedList[9];for (int i=0;i<rankList.length;i++){rankList[i]=new LinkedList();}

第一次处理按大小分成9个点数分为九段链表

 //把数据一个一个的放入到对应的组中while(list.size()>0){//取一个Mahjong m=list.remove();//放到组中rankList[m.rank-1].add(m);}//把9个组合到一起for (int i = 0; i < rankList.length; i++) {list.addAll(rankList[i]);}

第二次按花色进行拆分

//先花色数进行分组LinkedList[] suitList=new LinkedList[3];for (int i=0;i<suitList.length;i++){suitList[i]=new LinkedList();}//把数据一个一个的放入到对应的组中while(list.size()>0){//取一个Mahjong m=list.remove();//放到组中suitList[m.suit-1].add(m);}//把3个组合到一起for (int i = 0; i < suitList.length; i++) {list.addAll(suitList[i]);}

先可以按花色在按点数进行分组，都是可以的，主要是按单链表顺序排序的结构

双链表

这里的查找删除，主要是可以借助于linkedlist的源码，也是双向链表的

/*** 在最后添加* @param e*/private void linkLast(E e) {Node<E> newNode = new Node<E>(last, e, null);Node<E> l = last;last = newNode;if (l == null) {first = newNode;}else {l.next = newNode;}size ++;}

/*** �在index的位置上添加一个元素* @param index* @param e*/public void add (int index, E e) {if(index < 0 || index >size) {return;}if (index == size) {linkLast(e);} else {Node<E> target = node(index);Node<E> pre = target.prev;Node<E> newNode = new Node<E>(pre, e, target);//			pre.next = newNode;
//			pre = newNode;//要考虑index=0时的情况if(pre == null) {first = newNode;} else {pre.next = newNode;}pre = newNode;size++;}}

主要注意点，在添加删除节点时，和单链表的区别，要考虑前后节点都要修改

参考分析可以看看我的linkedlist的源码分析

Java 集合深入理解（二）：LinkedList链表源码研究，及双向队列如何实现