回溯法之圆排列问题

article/2025/9/20 20:18:53

问题描述

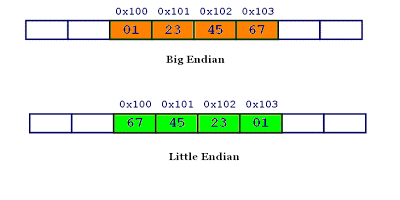
给定n个大小不等的圆c1,c2,…,cn，先要将这n个圆排进一个矩形框中，且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。例如，当n=3时，且所给的3个圆的半径分别为1、1、2时，这3个圆的最小长度的圆排列如图所示，其最小长度为2+4*√2.
在这里插入图片描述

算法设计

这个问题的解空间应该是一棵排列树。因为圆就是按照一定的顺序排在矩形框中的，这里面我们将圆的半径进行排序，从而代表圆排序。其中a=[r1,r2,…,rn]就是我们的序列。
CirclePerm(n,a)返回找到的最小圆排列长度。初始时，数组a是输入的n个圆的半径，计算结束后返回相应于最优解的圆排列。Center计算当前所选择的圆在当前圆排列中圆心的横坐标，Compute计算当前圆排列的长度，变量min记录当前最小圆排列的长度，数组r表示当前圆排列，数组x则记录当前圆排列中各圆的圆心横坐标。算法中约定在当前圆排列中排在第一个的圆的圆心横坐标为0.
在递归算法中，当i>n时，算法搜索至叶结点，得到新的圆排列方案。此时算法调用Compute计算当前圆排列的长度，适时更新当前最优值。
当i<n时，当前扩展结点位于排列树的第i-1层。此时算法选择下一个要排列的圆，并计算相应的下界函数。在满足下界约束的结点处，以深度优先的方式递归地对相应子树搜索(此结点为扩展结点)。对于不满足下界约束的结点，剪去相应的子树。
至于下界约束如何计算呢？我们用一个图来说明：
在这里插入图片描述

代码

#include <math.h>
#include <iostream>
using namespace std;
class Circle
{friend float CirclePerm(int,float *);private:float Center(int t);//计算当前所选择圆的圆心横坐标void Compute(void);void Backtrack(int t);float min,//当前最优值*x,//当前圆排列圆心横坐标*r;//当前圆排列(可理解为半径排列)int n;//待排列圆的个数float Circle::Center(int t){float valuex,temp = 0;//之所以从1-t判断是因为防止第t个圆和第t-1个圆不相切for(int j = 1;j < t;j++){valuex = x[j] + sqrt(r[t] * r[j]);if(valuex > temp)temp = valuex;}return temp;}void Circle::Compute(void){float low = 0,high = 0;for(int i = 1;i <=n;i++){if(x[i] - r[t] < low){low = x[i] - r[i];}if(x[i] + r[i] > high){high = x[i] + r[i];}}if(high - low < min)min = high - low;}void Circle::Backtrack(int t){if(t > n){//到达叶子节点,我们计算high与low的差距Compute();}else{//排列树解空间for(int j = 1;j <= t;j++){//圆的排列其实就是就是半径的排列,因为相同半径的圆是相同的//交换半径顺序,可以进一步优化,如果半径相等不交换//镜像序列只算一次,例如1,2,3和3,2,1swap(r[t],r[j]);if(Center(t)+r[1]+r[t] < min)//下界约束,我们取第一个圆的圆心为原点,所以计算距离的时候要加上r[1]和r[t]{x[t] = Center(t);Backtrack(t+1;)}swap(r[t],r[j]);}}}float CirclePerm(int n,float *a){Circle X;X.n = n;X.r = a;X.min = 100000;float *x = new float [n+1];//圆的中心坐标排列X.x = x;X.Backtrack(1);delete[] x;return X.min;}
};