圆排列问题详解（原理+代码）

问题描述

给定n个大小不等的圆c1,c2,…,cn，现要将这n个圆排进一个矩形框中，且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。
在这里插入图片描述

问题分析

圆排列问题的解空间是一棵排列树，我们用回溯法在整个排列数中搜索最优解。
首先，我们可以把这个问题分解为以下几步：

找出所有圆的排列
计算出每一个排列的长度
选择最小的长度

那么我们分三个步骤讨论下：

全排列

给你一组半径，每个代表一个圆，找出所有的排列方式。这其实就是全排列问题。
我们用递归的方法找出全部的排列。
比如：给你abc
其实你很容易写出他的全排列 abc acb bac bca cab cba
你可能有很多种方法来写出，这里讲解一种。
以abc为例，其长度为3，那么我们可以看做有三个空，你可以使用abc来填数。
那么面对第一个空的时候，你可以选a或者b或者c
假如你选了a，那么面对第二个空的时候，你可以选b或者c，假如你选了b，那么第三个空你只能选c
这样你可以选择出所有的排列
在这里插入图片描述

那么我们把这个操作用交换来实现试试
给你abc，分别在第一个位置，第二个位置和第三个位置。
那么第一个空（也就是第一个位置）应该填的有三种可能（可能a 可能b 可能c）
那我们就用第一个位置与第一、第二、第三个位置依次交换，就代表了依次选择。
那么当第一个位置的值与第二个位置交换的时候。得到了bac，此时就代表我们选定的第一个位置的字符为b，接下来的处理其实可以看作：剩下两个位置，剩下两个字符，找出他们的全排列。那岂不是可以还用刚才的方法，拿第二个位置的值与第二、第三位置分别交换，以此类推，就找到了所有的全排列。
在这里插入图片描述

需要注意的是，每次交换选定后，递归搜索出他后面字符的全排列后，还需要把该字符交换回去。举个例子，abc，a和b交换之后，说明第一个位置选定了a了。然后递归找以a为首的排列，全找出来之后，还得把a和b换回去，因为下面我们要把a和c交换，找以c为开头的全排列。这就是代码里面两次交换的原因。

代码：

int r[1000];//r里面存放了给定的一组数字
int N;//N代表这组数字的长度
int index=1;//index初始从1开始
void backtrack(int index){ //if(index==N+1){//已经找到了一个排列//存放在r数组中 输出r数组即可}else{for(int j=index;j<=N;j++){//index之前的已经排列好 index位置依次与后面位置的值交换 swap(r[index],r[j]);backtrack(index+1);//确定index之后，递归寻找index之后字符的全排列 swap(r[index],r[j]);//index选择j的情况已经结束 把他换回去 进行下一个交换 }}
}

计算一种排列的长度

找出了所有的排列
那么只要我们能够计算出一种排列的长度
那么所有的排列比较一个最小的即可得到答案
怎么算呢，我们已经有了半径信息。那么假设前一个圆的圆心横坐标为x1，后一个是x2，半径是r1和r2
那么r1和r2做差就是直角边（每一个圆都与底框相切），r1+r2就是斜边，那么根据勾股定理即可计算出x
$x^2 = sqrt((r_1+r_2)^2-(r_1-r_2)^2)$ 推导出x = 2sqrt(r1r2)
x1+x就是x2，那么有了这个公式，我们假定第一个圆形的圆心横坐标为0，知道了第一个就能算出第二个，以此类推所有的圆心横坐标就都算出来了。
在这里插入图片描述

有了所有的横坐标，还有该排列所有圆的半径，那么第一个圆的横坐标加上第一个圆的半径就是该排列的最左边low
最后一个圆的横坐标加上最后一个圆的半径就是该排列的最右边high
在这里插入图片描述

high-low即可得到长度。

完善算法

前面的想法其实还存在一些问题。计算横坐标x的时候，我们使用的公式有一个前提，就是这个圆必须和前一个圆相切，那么实际情况中是相切的嘛
在这里插入图片描述

如图，是不一定的。当前圆并不一定与前一个圆相切，有可能和前一个相切，也有可能和前面任意一个圆相切。所以，我们其实需要和前面所有的圆都进行一次计算。如图，这个圆和前面相邻的那个并不相切，所以你用我们说的那个公式计算的话，会计算出来偏小的结果。所以我们只需要把当前圆与前面所有的圆依次计算，保留最大的值，就是正确的值。
还有一个问题：
我们计算左右边界的方法是对的吗？
左边界并不一定是第一个圆的左边
在这里插入图片描述

如图，左边界并不是第一个圆的左边，那么怎么算呢
其实我们有了每个圆的圆心横坐标和半径了，我们只要把每个圆的左边界算出来，取最小的就是整个排列的左边界了
同理，把每个圆的右边界算出来，取最大的，就是整个排列的右边界了

剪枝（回溯）

在搜索过程中，如果当前位置的排列长度已经大于维护的最小值了，那就不用继续搜索子树了
所以可以剪个枝

void backtrack(int index){if(index==N+1){//已经找到了一个排列compute();}else{for(int j=index;j<=N;j++){//index之前的已经排列好 index位置依次与后面的交换 swap(r[index],r[j]);double center_x=center(index);//计算当前第t个位置的横坐标if(center_x+r[index]+r[1]<minlen){//如果已经大于维护的最小值 则不必搜索 x[index]=center_x;//存入表示坐标的数组x中backtrack(index+1);//递归选择index+1位置 }swap(r[index],r[j]);//index选择j的情况已经结束 把他换回去 进行下一个交换 }}
}

代码实现

#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
#define MAXLEN 1000
double r[MAXLEN];//存放圆排列的半径
double x[MAXLEN];//存放圆排列的圆心横坐标
double best_r[MAXLEN];//用来记录结果
int N;//输入圆的个数 
double minlen=1000;void compute(){//找到了一个排列 且此半径排列存放在数组r中double low=0,high=0;for(int i=1;i<=N;i++){//算出每一个圆的左边界和右边界if(x[i]-r[i] < low) low = x[i]-r[i];if(x[i]+r[i] > high) high = x[i]+r[i]; }if(high-low<minlen){minlen=high-low;//更新最小长度for(int i=1;i<=N;i++) best_r[i]=r[i];//记录最小排列}
}double center(int t){//计算圆心坐标 double x_max=0;for(int j=1;j<t;j++){//t=1的时候 第一个圆不计算 横坐标记为0 double x_value=x[j]+2.0*sqrt(r[t]*r[j]);if(x_value>x_max) x_max=x_value;//取最大的那个计算值 } return x_max;
}void backtrack(int index){if(index==N+1){//已经找到了一个排列compute();}else{for(int j=index;j<=N;j++){//index之前的已经排列好 index位置依次与后面的交换 swap(r[index],r[j]);double center_x=center(index);//计算当前第t个位置的横坐标if(center_x+r[index]+r[1]<minlen){//如果已经大于维护的最小值 则不必搜索 x[index]=center_x;//存入表示坐标的数组x中backtrack(index+1);//递归选择index+1位置 }swap(r[index],r[j]);//index选择j的情况已经结束 把他换回去 进行下一个交换 }}
}
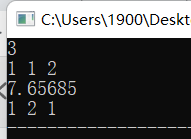
int main(){cin>>N;//一共N个圆 for(int i=1;i<=N;i++){cin>>r[i];//输入所有圆的半径}backtrack(1);//输出结果 cout<<minlen<<endl;for(int i=1;i<=N;i++) cout<<best_r[i]<<" ";return 0;
}

运行结果
在这里插入图片描述

算法优化：

复杂度：
在这里插入图片描述
优化：
（1）1,2,…,n-1,n和n,n-1, …,2,1这种互为镜像的排列具有相同的圆排列长度，可以计算一半，减少一半的计算量；
注意减少的是一半的计算量，全排列我们还是要搜索完的，你得找到叶子结点，才知道这个是重复的串。所以整体复杂度的数量级依然是O(n!)
（2）所给的n个圆中有k个圆有相同的半径，则这k个圆产生的k!个完全相同的圆排列，只需要计算一个。
这个可以减少搜索的排列数，但是极端情况没有改变。