一、算法灵感

蛇优化算法(Snake Optimization, SO)是2022年提出的一种元启发式优化算法，其灵感来源于蛇的交配行为。如果温度低，且食物充足，那么蛇就会相互交配，否则，蛇只会去寻找食物或吃现有的食物。依靠这些信息，将整个过程分为探索和开发。探索和开发之间的切换受环境因素影响，即温度和食物。

二、算法介绍

2.1 初始化

首先，SO会生成一个均匀分布的随机种群。初始种群可由以下公式求得：
${X_i} = {X_{\min }} + rand \times \left( {{X_{\max }} - \left. {{X_{\min }}} \right)} \right. \tag{1}$ 其中， ${X_i}$ 表示第 $i$ 个个体的位置， $r an d$ 是 $[0, 1]$ 之间的随机数， ${X_{min}}$ 、 ${X_{max}}$ 分别是问题的下界和上界。

2.2 划分种群

假设种群分为两组：雄性种群和雌性种群，其数量各占一半。用下面的两个公式(2)和(3)来划分群体。
${N_m} \approx N/2 \tag{2}$ ${N_f} = N - {N_m} \tag{3}$ 其中， $N$ 是种群中个体的数量， $N_m$ 指的是雄蛇数量， $N_f$ 指的是雌蛇数量。

2.3 定义温度和食物

温度 $T e m p$ 可以用下式定义。
$\exp \left( {{{ - t} \over T}} \right) \tag{4}$ 其中， $t$ 为当前迭代次数， $T$ 为最大迭代次数。
食物量 $Q$ 可用下式得到。
${c_1} * \exp \left( {{{t - T} \over T}} \right) \tag{5}$ 其中， $c_1$ 是常数，值为0.5。

2.4 食物不足时(探索阶段)

如果食物不足(阈值为0.25)，即 $Q < 0.25$ 时，蛇通过选择任意随机的位置来寻找食物，并更新它们的位置。对探索阶段进行建模，如下：
${X_{i,m}}\left( {t + 1} \right) = {X_{rand,m}}\left( t \right) \pm {c_2} \times {A_m} \times \left( {\left( {{X_{\max }} - {X_{\min }}} \right) \times rand + {X_{\min }}} \right) \tag{6}$ 其中， $X_{i,m}$ 为第 $i$ 条雄蛇的位置， $X_{rand,m}$ 为随机一条雄蛇的位置， $A_m$ 为雄蛇寻找食物的能力，其计算公式如下：
${A_m} = \exp \left( {{{ - {f_{rand,m}}} \over {{f_{i,m}}}}} \right) \tag{7}$ 其中， $f_{rand,m}$ 为 $X_{rand,m}$ 的适应度值， $f_{i,m}$ 是雄性种群中第 $i$ 条蛇的适应度值， $c_2$ 是常数，值为0.05。
${X_{i,f}} = {X_{rand,f}}\left( {t + 1} \right) \pm {c_2} \times {A_f} \times \left( {\left( {{X_{\max }} - {X_{\min }}} \right) \times rand + {X_{\min }}} \right) \tag{8}$ 其中， $X_{i,f}$ 是第 $i$ 条雌蛇的位置， $X_{rand,f}$ 是随机一条雌蛇的位置， $A_f$ 为雌蛇寻找食物的能力，其计算公式如下：
${A_f} = \exp \left( {{{ - {f_{rand,f}}} \over {{f_{i,f}}}}} \right) \tag{9}$ 其中， $f_{rand,f}$ 是 $X_{rand,f}$ 的适应度值， $f_{i,f}$ 是雌性种群中第 $i$ 条蛇的适应度值

2.5 食物充足时(开发阶段)

如果食物充足，且温度充足(阈值为0.6)，即 $Q > 0.25$ 且 $T e m p > 0.6$ 时，蛇只会向食物移动。
${X_{i,j}}\left( {t + 1} \right) = {X_{food}} \pm {c_3} \times Temp \times rand \times \left( {{X_{food}} - {X_{i,j}}\left( t \right)} \right) \tag{10}$ 其中， $X_{i,j}$ 是个体(雄蛇或雌蛇)的位置， $X_{food}$ 是最优个体的位置， $c_3$ 是常数，值为2。
如果食物充足，但温度不足，即 $Q > 0.25$ 且 $T e m p < 0.6$ 时，蛇将处于斗争模式或交配模式。

2.5.1 斗争模式

${X_{i,m}}\left( {t + 1} \right) = {X_{i,m}}\left( t \right) \pm {c_3} \times FM \times rand \times \left( {{X_{best,f}} - {X_{i,m}}\left( t \right)} \right) \tag{11}$ 其中， ${X_{best,f}}$ 为雌性种群中最优个体的位置， $FM$ 为雄蛇的战斗能力
${X_{i,f}}\left( {t + 1} \right) = {X_{i,f}}\left( {t + 1} \right) \pm {c_3} \times FF \times rand \times \left( {{X_{best,m}} - {X_{i,F}}\left( {t + 1} \right)} \right) \tag{12}$ 其中， ${X_{best,m}}$ 为雄性种群中最优个体的位置， $FF$ 为雌蛇的战斗能力。
$FM$ 和 $FF$ 的计算公式如下：
$\exp \left( {{{ - {f_{best,f}}} \over {{f_i}}}} \right) \tag{13}$ $\exp \left( {{{ - {f_{best,m}}} \over {{f_i}}}} \right) \tag{14}$ 其中， $f_{best,f}$ 为雌性种群中最优个体的适应度值， $f_{best,m}$ 为雄性种群中最优个体的适应度值， $f_i$ 为个体的适应度值

2.5.2 交配模式

${X_{i,m}}\left( {t + 1} \right) = {X_{i,m}}\left( t \right) \pm {c_3} \times {M_m} \times rand \times \left( {Q \times {X_{i,f}}\left( t \right) - {X_{i,m}}\left( t \right)} \right) \tag{15}$ ${X_{i,f}}\left( {t + 1} \right) = {X_{i,f}}\left( t \right) \pm {c_3} \times {M_f} \times rand \times \left( {Q \times {X_{i,m}}\left( t \right) - {X_{i,f}}\left( t \right)} \right) \tag{16}$ 其中， $M_m$ 和 $M_f$ 分别为雄蛇和雌蛇的交配能力，其计算公式如下：
${M_m} = \exp \left( {{{ - {f_{i,f}}} \over {{f_{i,m}}}}} \right) \tag{17}$ ${M_f} = \exp \left( {{{ - {f_{i,m}}} \over {{f_{i,f}}}}} \right) \tag{18}$ 如果蛋孵化，就用它们替换最差的雄蛇和雌蛇。
${X_{worst,m}} = {X_{\min }} + rand \times \left( {{X_{\max }} - {X_{\min }}} \right) \tag{19}$ ${X_{worst,f}} = {X_{\min }} + rand \times \left( {{X_{\max }} - {X_{\min }}} \right) \tag{20}$ 其中， $X_{worst,m}$ 为雄性种群中的最差个体， $X_{worst,m}$ 为雌性种群中的最差个体。

2.4 算法伪代码

初始化种群规模 $N$ ，迭代次数 $T$ ，等
随机初始化种群： $X_i(i=1,2,...,N)$
通过公式(2)和(3)将种群 $N$ 划分为2个数量相等的组 $N_m$ 和 $N_f$
While $t < T$ do
For(i=1 to N)do
For(j=1 to Dim)do
计算每组的适应度值 $f_i$
找到适应度最好的雄蛇 $X_{best,m}$
找到适应度最好的雌蛇 $X_{best,f}$
计算由公式(4)定义的温度 $T e m p$
计算由公式(5)定义的食物 $Q$
If $Q < 0.25$ then
使用公式(6)和(8)进行探索
Else If $T e m p > 0.6$ then
使用公式(10)进行开发
Else
If $r an d > 0.6$ then
使用公式(11)和(12)进行斗争
Else
使用公式(15)和(16)进行交配
使用公式(19)和(20)替换掉位置最差的雄蛇 $X_{worst,m}$ 和雌蛇 $X_{worst,f}$
End If
End If
End For
End For
$t = t + 1$
End While
返回最优解( $X_{food}$ )

三、实验结果

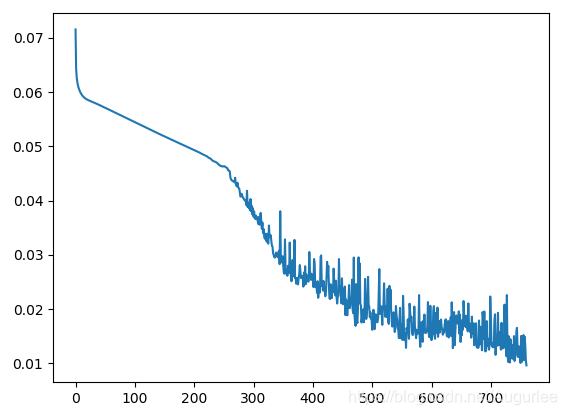
SO在23个经典测试函数(设置维度 $d im = 30$ )的F2、F8、F16中的收敛曲线，测试函数公式如下：

函数	公式	理论值
F2	${F_2}(x) = \sum\nolimits_{i = 1}^n {\left\| {{x_i}} \right\|} + \prod _{i = 1}^n\left\| {{x_i}} \right\|$	$0.00$
F8	${F_8}(x) = \sum\nolimits_{i = 1}^n { - {x_i}\sin (\sqrt {\|{x_i}\|} )}$	$- 418.9829 \times d im$
F16	${F_{16}}(x) = 4x_1^2 - 2.1x_1^4 + {1 \over 3}x_1^6 + {x_1}{x_2} - 4x_2^2 + x_2^4$	$- 1.0316$