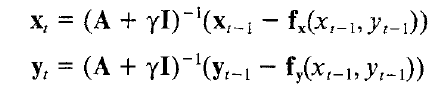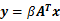1 能量泛函
在介绍snake模型的参考资料[1]中,提到能量泛函的概念,这里对此概念做一个总结。
参考资料[6]给出了泛函的定义: 简单的说, 泛函就是定义域是一个函数集,而值域是实数集或者实数集的一个子集。推广开来, 泛函就是从任意的向量空间到标量的映射。也就是说,它是从函数空间到数域的映射。简言之,泛函就是函数的函数。
参考资料[7]对上述的定义做了实例解析,更加容易理解。同时,参考资料[7]中提到了能量泛函(用泛函表示的能量),已经解析了能量泛函的梯度下降流的概念。
2 活动轮廓模型
参考资料[8]指出,活动轮廓模型是指定义在图像域上的曲线(曲面)在与曲线(曲面)自身相关的内力以及由图像数据定义的外力的共同作用下向物体边缘靠近的模型。外力推动活动轮廓“拉向”物体边缘或者其他感兴趣的图像特征,而内力则保持活动轮廓的光滑和连续性。
参考资料[1]通过介绍曲线演化理论,提出了两个问题:1)轮廓如何表示;2)力如何构造。
针对第1个问题,形成了两大流派:1)参数活动轮廓模型;2)几何活动轮廓模型。参考资料[8]对这两种模型进行了更为详细的说明。
2.1 参数活动轮廓模型——snake模型
参考资料[1]指出,如果轮廓是参数表示的,那么就是参数活动轮廓表示模型,典型为snake模型。
参考资料[8]给出更为详细的定义,参数活动轮廓模型,即snake模型,又称为基于变分法的活动轮廓模型。它直接以曲线(曲面)的参数化形式显式地表达曲线(曲面)的演化。它为给定的模型构造特定的能量函数,然后利用变分法对该能量函数极小化,得到模型演化的偏微分方程,使得轮廓线在到达目标边界时因为能量函数达到最小值而自动停止。
关于snake模型更为详细的说明,见参考资料[1][8]。
2.2 几何活动轮廓模型——水平集
参考资料[1]指出,如果轮廓是几何表示的,那么就是几何活动轮廓模型,即水平集方法。
参考资料[8]则指出,几何活动轮廓模型的初始轮廓是在轮廓曲线的几何特性(如曲率等)的推动下向着目标的边缘移动,而与轮廓的参数特性无关,避免了参数活动轮廓必须重复第参数化曲线这一难题。
由于引入了曲线(曲面)演化理论和水平集方法,将活动轮廓线间接表达为水平集函数的零水平集形式,从而可以非常自然地处理拓扑结构的变化,并且提供了稳定的数值算法。
2.2.1 曲线演化理论
参考资料[8]指出,曲线演化理论是指仅利用曲线的单位法矢和曲率等几何参数研究曲线随时间的变形,而这些几何参数与曲线的参数化方式无关。
参考资料[1]的作者认为,虽然曲线演化理论运用于水平集中,但是在主动轮廓模型中,这个知识是公用的。
2.2.2 水平集
参考资料[1][8]都提及水平集的概念,在参考资料[8]中更是详细的介绍。
参考资料[8]指出,在水平集方法中,平面闭合曲线C被隐含的表达为三维连续函数曲面


参考资料
[1]图像分割之(五)活动轮廓模型之Snake模型简介
[2]Snake模型在轮廓提取中的应用
[3]基于形态学和Snake模型的尿沉渣提取
[4]Snake模型算法的基本思想数学模型及工作原理
[5]Snake 模型
[6]泛函
[7][原创]理解泛函的概念和能量泛函的梯度下降流
[8]董吉文. 活动轮廓模型综述. 济南大学信息科学与工程学院. 2008年第5期
[9]李天庆等. Snake模型综述. 清华大学自动化系. 2005
[10]张辉等. 基于Snake模型的图像分割技术研究. 西安理工大学. 2008年
[11]田绪红等. 基于B_Snake的三维图像骨架化方法. 华南农业大学. 2008年
[12]曹治国等. 基于Snake模型的血管树骨架三维重建技术. 华中科技大学. 2010年