1. 回归（regression）

1.1 起源与定义

回归最早是被高尔顿提出的。他通过研究发现：如果父母都比较高一些，那么生出的子女身高会低于父母的平均身高；反之，如果父母双亲都比较矮一些，那么生出的子女身高要高于父母平均身高。他认为，自然界有一种约束力，使得身高的分布不会向高矮两个极端发展，而是趋于回到中心，所以称为回归。
目前，从用法角度将其定义为一种数值（scalar）预测的技术，区别于分类（类别预测技术）。

1.2 不同的用法

1.2.1 解释（Explanation）

回归可用于做实证研究，研究自变量和因变量之间的内在联系和规律，常见于社会科学研究中。

互联网的普及降低了教育不平等程度吗？
大学生就业选择的影响因素有哪些？
医疗电子商务场景下客户满意度的影响因素有哪些？

1.2.2 预测（Prediction）

回归也可用来做预测，根据已知的信息去准确预测未知的事情。

股市预测：根据过去10年股票的变动、新闻咨询、公司并购咨询等，预测股市明天的平均值。
商品推荐：根据用户过去的购买记录和候选的商品信息，预测用户购买某个商品的可能性。
自动驾驶：根据汽车的各个sensor的数据，例如路况和车距等，预测正确的方向盘角度。

1.3 模型的构建

无论目的是解释还是预测，都需要掌握与任务相关的规律（认识世界），即建立合理的模型。
不同的一点是，解释模型只需要基于训练集构建，一般具备解析解（计量经济模型）。预测模型必须在测试集上做检验和调整，一般不具备解析解，需要通过机器学习的方法去调整参数。因此，同样的模型框架和数据集，最优的解释模型和预测模型很可能是不相同的。
本文主要关注预测模型的构建，不涉及解释模型相关的内容。

2. 基于机器学习的模型构建

我们以Pokemon精灵攻击力预测这个任务为例，梳理机器学习三个步骤的详细内容。

输入：进化前的CP值、物种（Bulbasaur）、血量（HP）、重量（Weight）、高度（Height）
输出：进化后的CP值

2.1 模型假设 - 线性模型

为了方便，我们选择最简单的线性模型来作为完成回归任务的模型框架。我们可以使用单特征或者多特征的线性回归模型，后者会更加复杂，模型集合会更大。

为选择合理的模型框架，提前对数据集进行探索，观察变量间的关系是很有必要的，这将决定最终将哪些变量放入模型，以及是否需要对变量进行再次处理（二次项、取倒数等）。

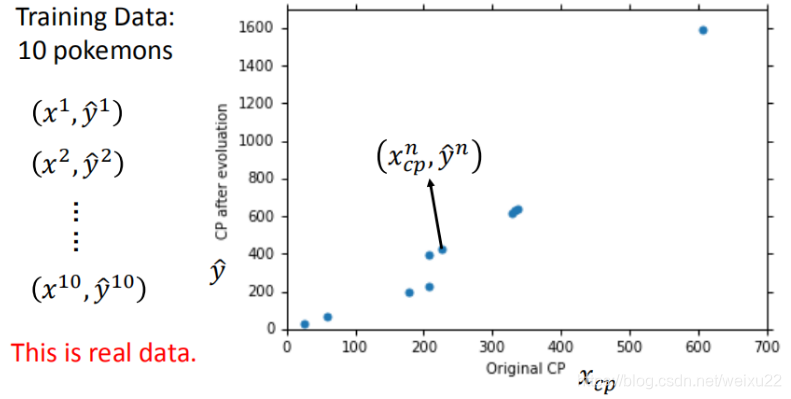
可以看出，横轴和纵轴主要呈直线关系，也有一些二次关系（可考虑加二次项）。
模型框架（预先设定） + 参数（待估计） = 模型（目标）
目前模型的参数包括各个特征的权重 $w_i$ 以及偏移量 $b$ 。

2.2 模型评价 - 损失函数

本文阐述的回归任务属于有监督学习场景，因此需要收集足够的输入输出对以指导模型的构建。

有了这些真实的数据，那我们怎么衡量模型的好坏呢？从数学的角度来讲，我们使用损失函数（Loss function）来衡量模型的好坏。Loss function基于模型预测值和实际值的差异来设置。

在本文中，我们选择常用的均方误差作为损失函数。

2.3 模型调优 - 梯度下降

当模型非凸时，是没有解析解的，只能通过启发式的方式迭代优化，常用的方法是梯度下降。

首先，我们随机选择一个 $w^0$ ，然后计算微分判定移动的方向，再更新对应参数，循环往复，直到找到最低点（两次更新之间差异小于阈值或者达到预先设定好的迭代次数）。
对于有多个待更新参数的模型，步骤是基本一致的，只不过做的是偏微分。

在梯度下降的过程中，会遇到一些问题，导致无法达到最优点。

这些问题如何解决以后会涉及到。

3. 模型构建中的问题和解决

3.1 评价模型的泛用性（Generalization）

好模型不仅要在训练集中表现优异，在未知的数据集（测试集，真实应用场景）中也应该一样。
因此，我们必须要计算模型在测试机上的性能，理想情况下不能有较大的下滑。

3.2 提高模型的拟合度

若模型过于简单，则模型集合较小，可能无法包含真实的模型，即出现欠拟合问题。
我们可以选择更复杂的模型去优化性能。以使用1元2次方程举例，显著提高了预测性能。

我们还可以在模型中增加调节项（Pokemon种类）来改进模型。
在这里插入图片描述

模型在训练集和测试集的性能表现如下所示：

3.3 防止过拟合（Overfiting）的出现

如果我们继续使用更高次的模型，可能会出现过拟合问题。

我们可以通过加入正则项来防止过拟合问题的出现。

正则项权重变化对模型性能的影响如下所示：

4. 回归 - 代码演示

现在假设有10个x_data和y_data，x和y之间的关系是y_data=b+w*x_data。b，w都是参数，是需要学习出来的。现在我们来练习用梯度下降找到b和w。

import numpy as np
import matplotlib.pyplot as plt
from pylab import mpl# matplotlib没有中文字体，动态解决
plt.rcParams['font.sans-serif'] = ['Simhei']  # 显示中文
mpl.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题# 生成实验数据
x_data = [338., 333., 328., 207., 226., 25., 179., 60., 208., 606.]
y_data = [640., 633., 619., 393., 428., 27., 193., 66., 226., 1591.]
x_d = np.asarray(x_data)
y_d = np.asarray(y_data)
x = np.arange(-200, -100, 1) # 参数的候选项，指偏移项b
y = np.arange(-5, 5, 0.1) # 参数的候选项，指权重w
Z = np.zeros((len(x), len(y)))
X, Y = np.meshgrid(x, y)# 得出每种可能组合下的loss，共需要计算100*100=10000次
for i in range(len(x)):for j in range(len(y)):b = x[i]w = y[j]Z[j][i] = 0  # meshgrid吐出结果：y为行，x为列for n in range(len(x_data)):Z[j][i] += (y_data[n] - b - w * x_data[n]) ** 2Z[j][i] /= len(x_data)

以上代码生成了实验数据，并用穷举法计算出了所有可能组合的loss，其中最小值为10216。
接下来我们尝试使用梯度下降法来快速寻找到较小的loss值。

# linear regression
b=-120
w=-4
lr = 0.000005
iteration = 10000 #先设置为10000b_history = [b]
w_history = [w]
loss_history = []
import time
start = time.time()
for i in range(iteration):m = float(len(x_d))y_hat = w * x_d  +bloss = np.dot(y_d - y_hat, y_d - y_hat) / mgrad_b = -2.0 * np.sum(y_d - y_hat) / mgrad_w = -2.0 * np.dot(y_d - y_hat, x_d) / m# update paramb -= lr * grad_bw -= lr * grad_wb_history.append(b)w_history.append(w)loss_history.append(loss)if i % 1000 == 0:print("Step %i, w: %0.4f, b: %.4f, Loss: %.4f" % (i, w, b, loss))
end = time.time()
print("大约需要时间：",end-start)
# Step 0, w: 1.6534, b: -119.9839, Loss: 3670819.0000
# Step 1000, w: 2.4733, b: -120.1721, Loss: 11492.1941
# Step 9000, w: 2.4776, b: -121.6771, Loss: 11435.5676

可以发现，梯度下降法可以快速从初始值迭代到合适的参数组合，接近最优参数。但我们发现，达到最优值的过程却非常缓慢。使用下面的代码可以对寻优过程进行可视化。

# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet'))  # 填充等高线
plt.plot([-188.4], [2.67], 'x', ms=12, mew=3, color="orange") # 最优参数
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(-200, -100)
plt.ylim(-5, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()