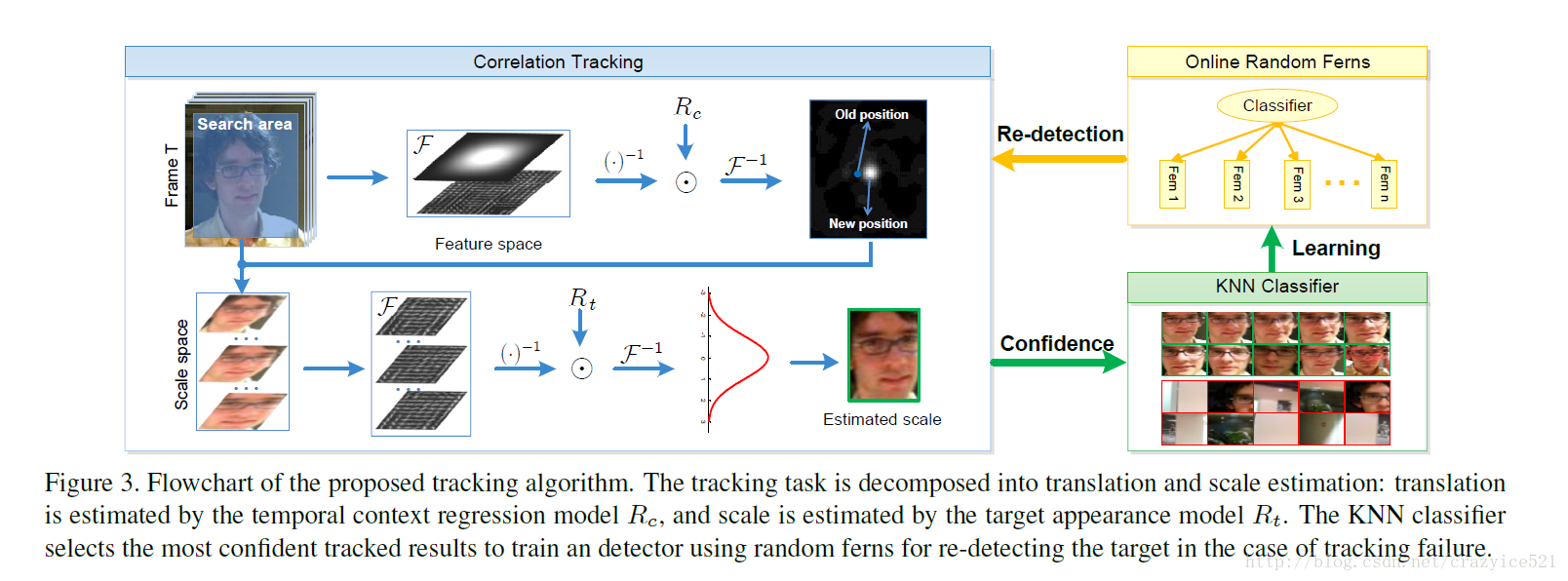
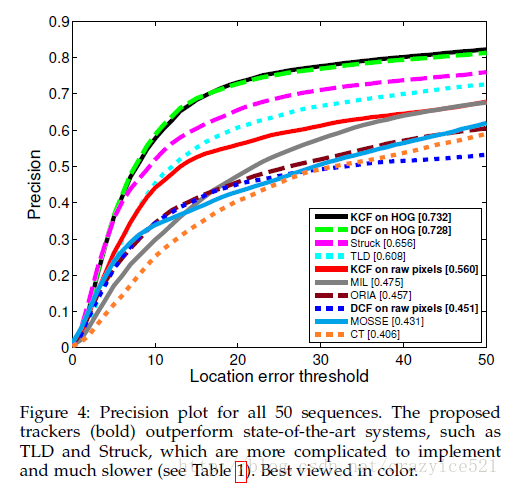
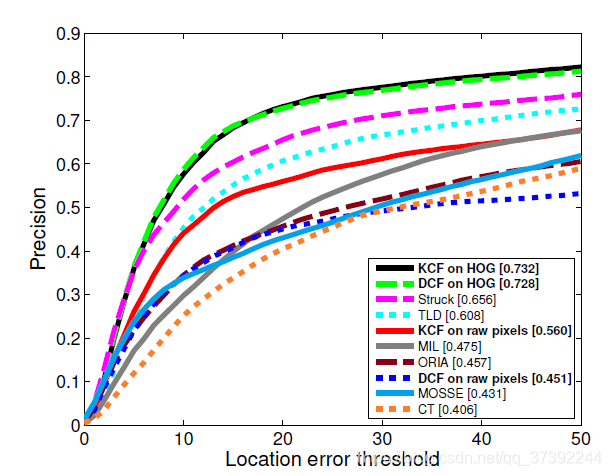
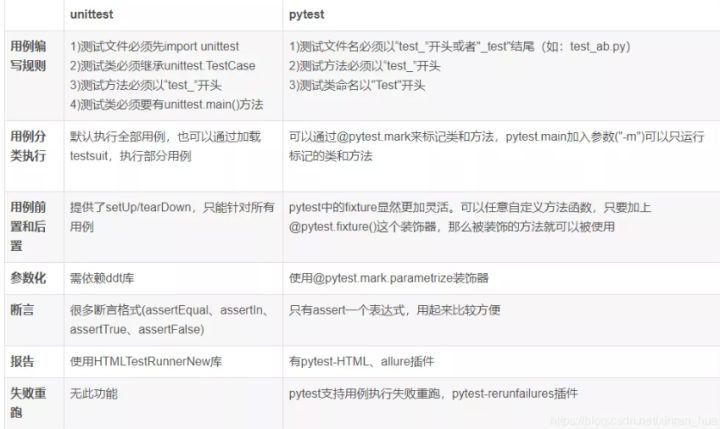
本文是CSK与KCF算法推导的第四篇，主要介绍将前面推导采用的一维情况推广到二维。

• CSK与KCF算法推导（一）——DFT、相关运算和循环卷积
• CSK与KCF算法推导（二）——带核函数的岭回归问题求解
• CSK与KCF算法推导（三）——算法主体部分推导
• （本文）CSK与KCF算法推导（四）——从一维推广到二维
• CSK与KCF算法推导（五）——具体实现细节
• CSK与KCF算法推导（六）——HOG特征提取与多通道计算

  KCF全文的推导都是建立在一维样本上的，但是实际使用却是用于二维的图像。那么它是怎样从一维推广到二维的呢？本文参照一维推导的思路给出二维的推导过程。

矩阵内积与矩阵的迹

  二维的推导，需要定义一些新的运算。$A$和$B$都是$m\times n$的矩阵，数学上有$\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{c}\mathrm{e}(A^{T}B)$表示矩阵对应位置元素相乘并求和的结果。参考向量内积，为了方便起见，定义两个矩阵的内积$<A,B>$，$A$和$B$都是$m\times n$的矩阵。它们两个的内积就是矩阵中对应位置的数相乘再相加。
$$<A,B>:=\mathrm{trace}(A^{T}B)$$

矩阵阵列

  用$[\cdot ]$表示矩阵阵列，矩阵阵列是一个四维的结构，就是矩阵里面嵌套矩阵。$[\cdot {]}_{uv}$表示矩阵阵列中的每个矩阵。

矩阵阵列和矩阵的乘法

  定义矩阵阵列和矩阵的乘法，用$\circ$表示。如下图所示：

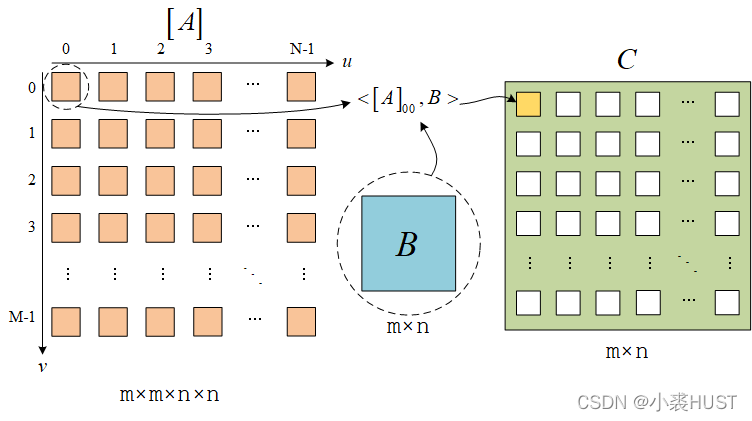
  一个矩阵阵列$[A]$和一个矩阵$B$相乘，就是矩阵阵列$[A]$中的每个矩阵和$B$内积，然后结果放到对应的位置，得到一个新的矩阵。
$$[A]\circ B=CC(x,y)=<[A{]}_{xy},B>$$

矩阵阵列和矩阵阵列的乘法

  矩阵阵列和矩阵的乘法，类似于矩阵和列向量的乘法。自然，类似于矩阵和矩阵的乘法，我们也能有矩阵阵列和矩阵阵列的乘法。

  矩阵阵列$[A]$依次和矩阵阵列$[B]$中的每个矩阵相乘，然后就能得到一个矩阵阵列$[C]$
$$[A]\circ [B{]}_{uv}=[C{]}_{uv}$$

矩阵分裂

  两个列向量的哈达玛积可以写成对角矩阵和列向量相乘的形式，两个矩阵的哈达玛积也可以写成一个矩阵阵列和矩阵相乘的形式。

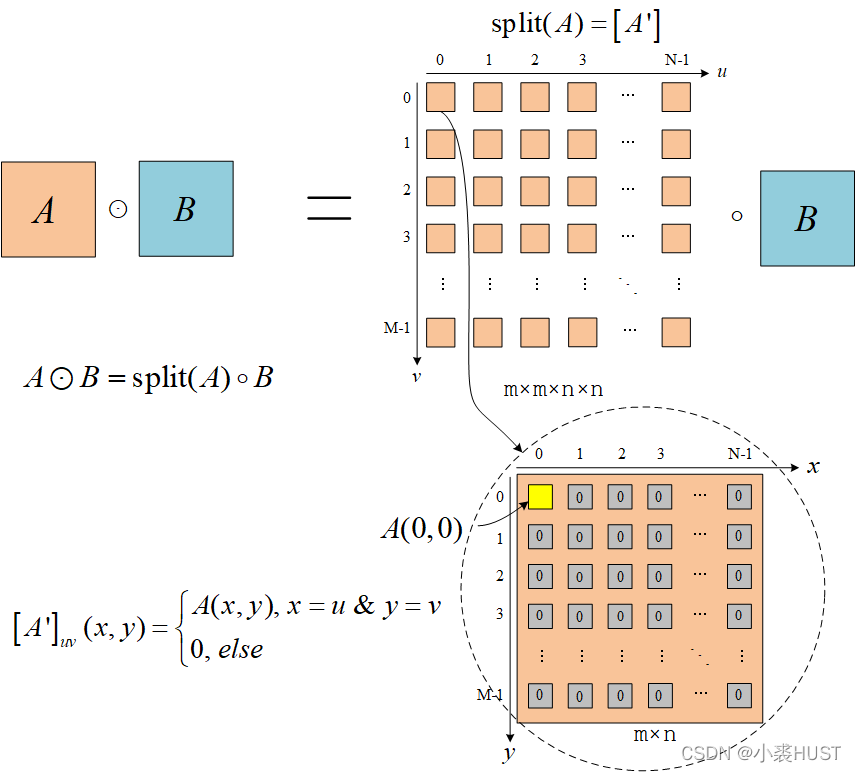
  定义$\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{i}\mathrm{t}()$函数，它可以将一个矩阵中的所有元素分散到矩阵阵列中的每个矩阵中去。类似于$\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{g}()$的过程。

单位矩阵阵列

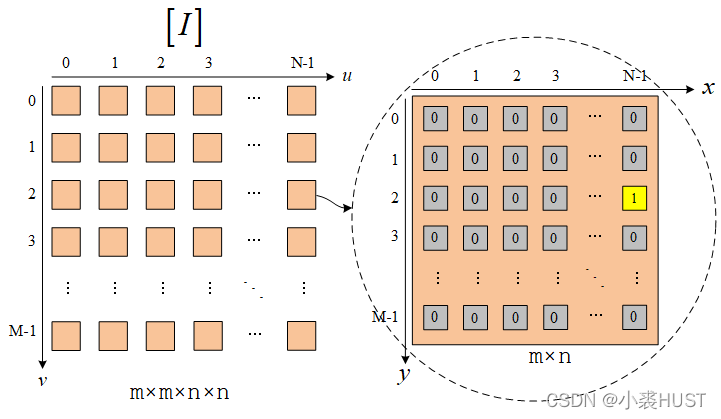
  单位矩阵阵列指的是满足以下条件的矩阵阵列：
$${\left[I\right]}_{uv}(x,y)=\{\begin{array}{c}1,x=u\&y=v\\ 0,else\end{array}$$

二维DFT的矩阵阵列表示

  首先给出二维DFT运算的式子。有一个矩阵m×n的矩阵$A(x,y)$，它的二维DFT结果为$\hat{A}(u,v)$。
$$\hat{A}(u,v)=\sum _{y=0}^{M-1}\sum _{x=0}^{N-1}A(x,y)W_N^{ux}{W}_M^{vy}$$

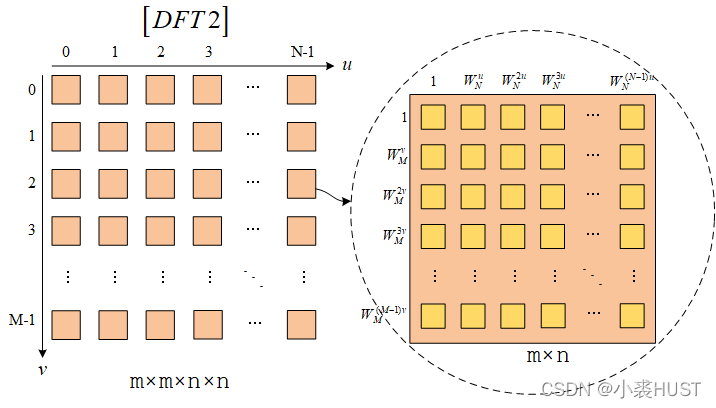
  根据二维DFT的计算公式，我们可以直接画出二维DFT对应的矩阵阵列$[DFT2]$。上图中右边每个黄色方框内的值是对应的行列旋转因子相乘。类似一维情况下的推导，我们可以得出：
$$\left[DFT2\right]\circ {\left[DFT2\right]}^{\ast }=MN\left[I\right]$$
$$\left(\frac{1}{\sqrt{MN}}\left[DFT2\right]\right)\circ \left(\frac{1}{\sqrt{MN}}{\left[DFT2\right]}^{\ast }\right)=\left[I\right]$$

二维相关运算

  首先给出二维的相关运算：
$$f(x,y)=\sum _{q=0}^{M-1}\sum _{p=0}^{N-1}A(p,q)B\left(x+p,y+q\right)$$
$$F(u,v)=\sum _{y=0}^{M-1}\sum _{x=0}^{N-1}\sum _{q=0}^{M-1}\sum _{p=0}^{N-1}A(p,q)B\left(x+p,y+q\right)W_N^{ux}{W}_M^{vy}$$
$$F(u,v)=\sum _{q=0}^{M-1}{W}_M^{-vq}\sum _{p=0}^{N-1}A(p,q)W_N^{-up}\sum _{x=0}^{M-1}{W}_M^{v(y+q)}\sum _{y=0}^{N-1}B\left(x+p,y+q\right)W_N^{u(x+p)}={\hat{A}}^{\ast }(u,v)\hat{B}(u,v)$$
  二维相关运算也可以用二维DFT加速。

循环矩阵阵列

  类似论文中提出的循环矩阵，这里我们定义循环矩阵阵列$C(A)$，由m×n的矩阵$A$通过循环移位产生。

• 定义算符$P^i$，$P^{i}A$表示矩阵$A$在沿着$x$正方向整体循环移位$i$个单位；
• 定义算符$Q^i$，$Q^{i}A$表示矩阵$A$在沿着$y$正方向整体循环移位$i$个单位；
  $$C(A{)}_{uv}=P^u{Q}^{v}A$$

  这个图太难画了，但我觉得这应该不难理解，就和一维的向量循环移位构成矩阵类似，矩阵循环移位构成矩阵阵列。
  $C(A)\circ B$表示的就是相关运算。这里我没有用二维卷积是因为我没想到怎样在矩阵阵列里定义对应的转置运算
$$C(A)\circ B=\left[IDFT2\right]\circ \left({\hat{A}}^{\ast }\odot \hat{B}\right)=\left[IDFT2\right]\circ \mathrm{split}({\hat{A}}^{\ast })\left(\left[DFT2\right]\circ B\right)$$
$$C(A)=\left[U^{\ast }\right]\circ \mathrm{split}({\hat{A}}^{\ast })\circ \left[U\right]U=\frac{1}{\sqrt{MN}}\left[DFT2\right]$$
  所以循环矩阵阵列也能够用DFT实现“分裂化”，即基础矩阵的二维DFT得到的结果分散到矩阵阵列的每个小矩阵中。正是因为能够做这样的特征分解，才有后面的element-wise的运算。
  后面我推不下去了，二维的岭回归大概是每个样本都是一个矩阵，所有样本排列在一起构成矩阵阵列，样本的标签值是一个二维函数，要优化的目标$\omega$也是一个二维的矩阵……

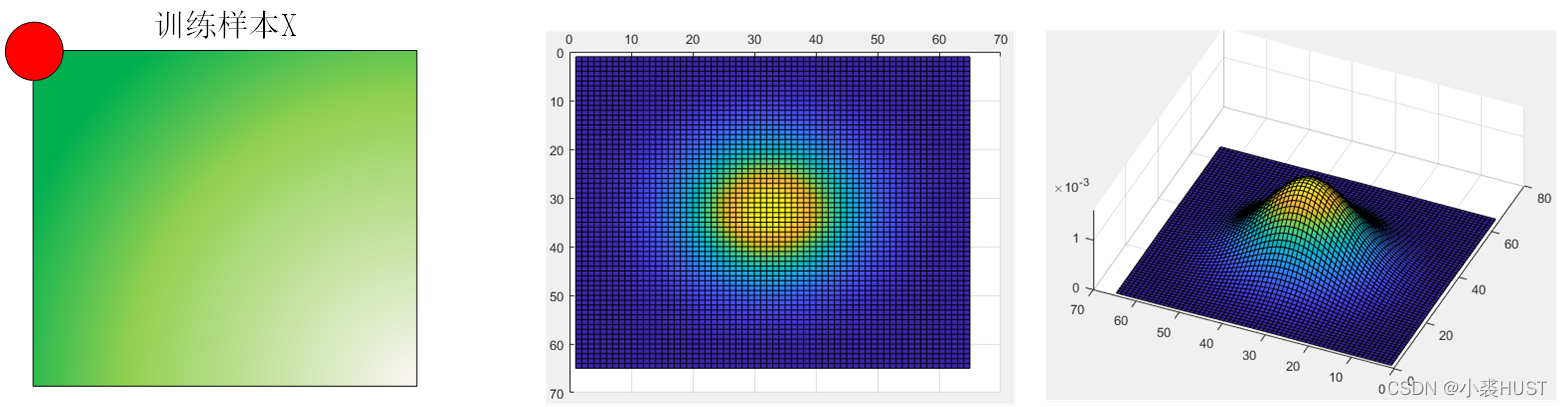
训练标签

  左上角第一个点表示样本不发生循环移动，如果用二维高斯函数作为训练标签，而且一开始我们关心的目标在训练样本图像的正中央，那么二维标签的左上角才是峰值点，因为左上角对应的位移量为0。又因为是循环移位的结构，所以四个角落都是峰值。

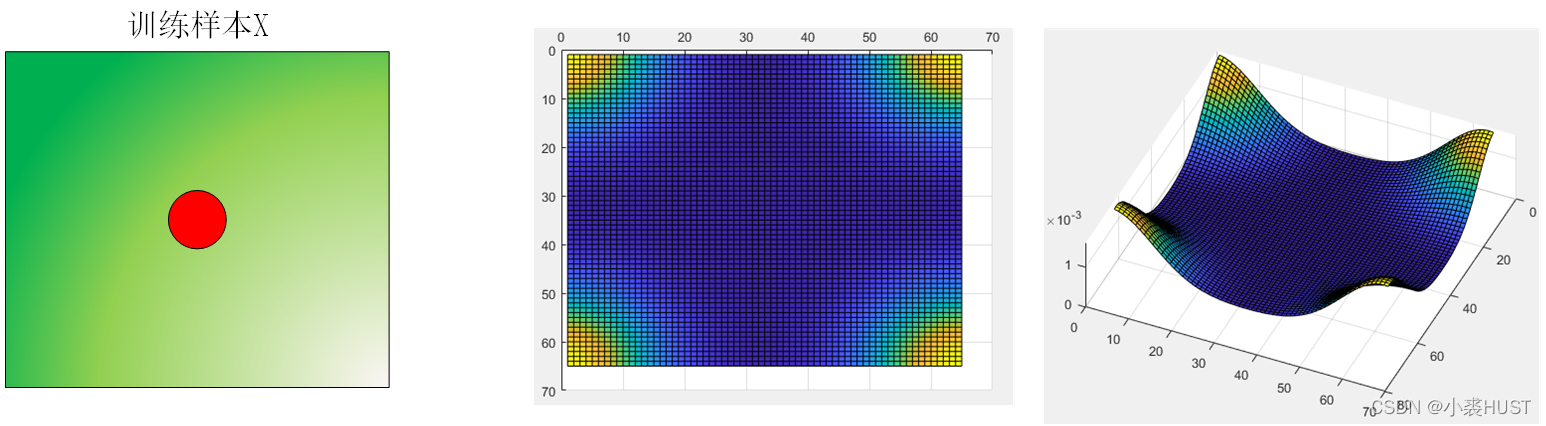
  如果我们关心的目标在样本图像的左上角，那么这个训练样本需要向左和向下平移一半的图像大小才能将样本移动到正中央，那样对应的二维高斯标签就是峰值在中央的情况。但这样做是不合理的，因为如果目标在左上角，那么目标周围的上下文信息就是残缺的。在做DFT之前为了保持周期的连续性，防止频谱泄露，还需要在给样本加窗。那样在左上角的目标信息就会丢失。
  所以如果目标是在训练样本的正中央的话，二维标签的峰值一定是在四个角落上。