思考两个问题
- 电报发送:二战的时候大家都知道那时候普遍会应用电报,如果让你来设计一个电报的发送编码你该如何设计呢?
- 电报加密后越短越好,发送快。
- 破解难
- 解码容易
- 换加密树也要快
- 可逆的
-
压缩算法:给你10000个字符(每个字符1btye,也就是8bit)的文件,你怎么存储可以尽可能的节省空间呢?假设字符是 a b c d 4种,10000 * 8 =80000bit
思路1:重复的去掉;思路2:使用二进制代替
假定 a=000 b=001 c=010 d=100,这样我们每个字符由于原来8bit就变成了3bit的二进制,缩小了将近3倍
举例分析:dab二进制为100000001,若是abcdaaa二进制为000001010100000000000,出现很多重复的a是否可以进一步优化?
假设优化:A:0 B:001 C:010 D:100,则abcdaaa:0001010100000=>abcdaaa进一步将重复的数据缩小了,是否存在问题?
abcdaaa解码,以前3个bit表示一个字符,现在b、c编码包含a,不支持解码,怎么优化?优化思路:区分开a和b,赫夫曼编码(前缀编码)
优化:A:0 B:101 C:110 D:100,则abcdaaa编码0101110100000
解码伪代码如下
// A:0 B:101 C:110 D:100
Map mapping;
String code="01011101000000000"
var decode;
var currDecode;
for(int i=0;i<code.lenth;i++){currDecode+=char(i);var res = mapping.get(currDecode);if(res != null){decode+=res}
}
最优二叉树(哈夫曼树)
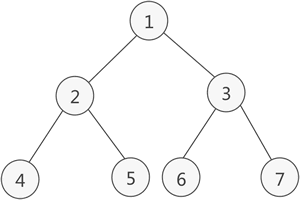
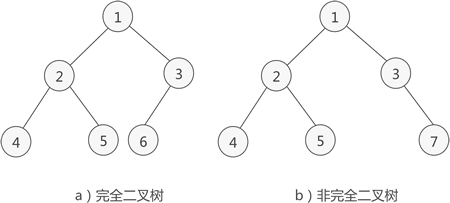
| 满二叉树 | 除了叶子节点,其他的都有两个子节点,1 2 4 8这样的节点 2^n个点
 |
|
| — | — |
| 完全二叉树 | 除了最底层都有两个子节点,而且叶子节点是靠左连续的
 |
|
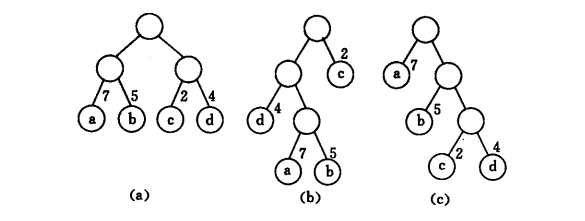
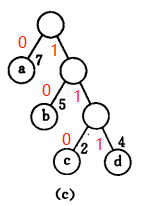
计算这三颗二叉树的带权路径长度总和:其中每个点的权重为:a:7 b:5 c:2 d:4
公式:每个节点深度*权重的和
WPL(a):72+52+22+42=36()
WPL(b):73+53+21+42=46()
WPL©:71+52+23+43=35()
发现什么? 权重越大节点,深度越低,和越小,和最小的就是最优二叉树
定义:
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近
那么这个赫夫曼树和压缩又有什么关系呢?
二叉树,二叉,这时候你要想到二进制,二叉分左右嘛。左节点的边设置为0,右节点的边设置为1
哈夫曼编码定义:
最优二叉树中我们给每一条边加上一个权值,指向左子节点的边我们标记为0,指向右子节点的边标记为1,那从根节点到叶节点的路径就是我们说的哈夫曼编码
所以图c的赫夫曼树对应的编码就是:
a:0 b:10 c:110 d:111
构建思路
核心思想:贪心算法:利用局部最优推出全局最优,把频率出现多的用短码表示,频率出现小的就用长一点。而且,任何一个字符的编码都不是另一个的前缀,在解压缩的时候,我们每次会读取尽可能长的可解压的二进制串,所以在解压缩的时候也不会产生歧义
具体实现思路:
- 按权重排序
- 每次取数值最小的两个节点,将之组成为一颗子树。
- 移除原来的两个点
- 然后将组成的子树放入原来的序列中
- 重复执行1 2 3 直到只剩最后一个点
实现哈夫曼树
例子: a:3 b:24 c:6 d:20 e:34 f:4 g:12,根据以上权重来实现哈夫曼树
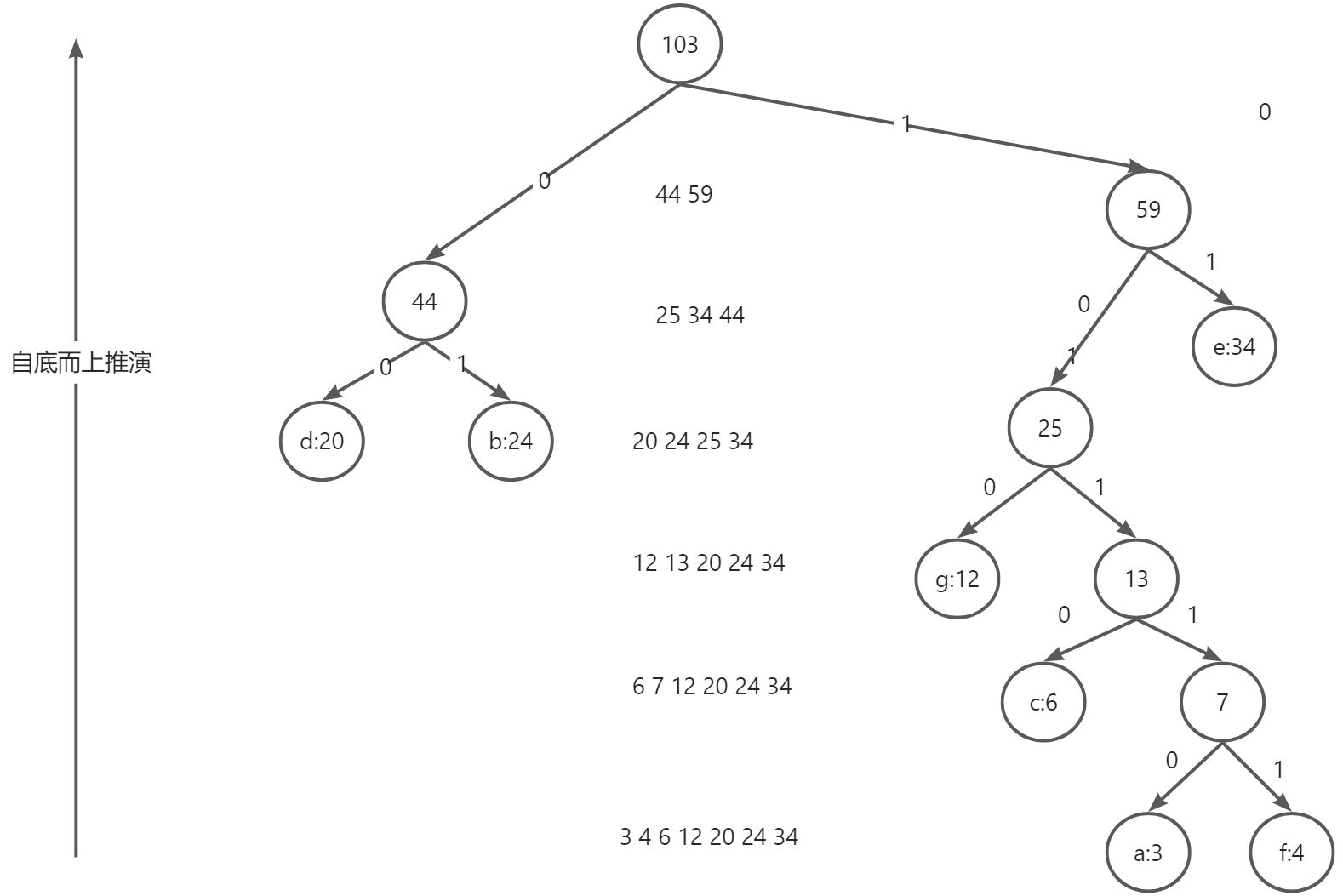
构建哈夫曼树
package datastructure.tree;import java.util.*;/*** 哈夫曼树** @author zw* @create 2023-04-09 1:24*/
public class HuffmenTree<T extends Comparable<T>> {MyTreeNode<T> root;List<MyTreeNode<T>> leafs; // 叶子节点Map<T, Integer> weights; // 叶子节点的权重, a,b,c,d,eMap<String, String> encodeMap = new HashMap<>(); // 编码表Map<String, String> decodeMap = new HashMap<>(); // 解码表public HuffmenTree(Map<T, Integer> weights) {this.weights = weights;leafs = new ArrayList<>();}/*** 构建哈夫曼树*/public void builder() {// 按权重排序,这可以用之前写得排序算法,为了方便使用jdk的优先队列PriorityQueue<MyTreeNode> priorityQueue = new PriorityQueue<MyTreeNode>((o1, o2) -> o1.weight - o2.weight);weights.forEach((data, weight) -> {MyTreeNode MyTreeNode = new MyTreeNode(data, weight);priorityQueue.add(MyTreeNode);leafs.add(MyTreeNode);});MyTreeNode root = null;while (priorityQueue.size() != 1) {// 从优先队列拿出最小的两个节点合并MyTreeNode leftNode = priorityQueue.poll();MyTreeNode rightNode = priorityQueue.poll();// 将合并节点放入优先对垒int parentNodeWight = leftNode.weight + rightNode.weight;MyTreeNode<T> parentNode = new MyTreeNode<T>(null, parentNodeWight);parentNode.left = leftNode;parentNode.right = rightNode;leftNode.parent = parentNode;rightNode.parent = parentNode;priorityQueue.add(parentNode);root = parentNode;}// 将根节点返回this.root = root;}/*** 解码* @param code* @return*/public String decode(String code) {String decode = "";char[] chars = code.toCharArray();String currCode = "";for (int i = 0; i < chars.length; i++) {currCode += chars[i];if (decodeMap.containsKey(currCode)) {String data = decodeMap.get(currCode);decode += data;currCode = "";}}return decode;}/*** 对输入编码** @param input*/public String encode(String input) {String code = "";for (char data : input.toCharArray()) {String encode = encodeMap.get(String.valueOf(data));code += encode;}return code;}/*** 对叶子节点编码** @return*/public void leafencode() {// 两种方式:1、自顶向下 2、自底向上,这儿采用自底向上for (MyTreeNode<T> leaf : leafs) {String code = "";T data = leaf.data;MyTreeNode currNode = leaf;while (currNode.parent != null) {// 判断当前节点,是左是右MyTreeNode parentNode = currNode.parent;if (parentNode.left == currNode) {code = "0" + code; // 自底向上编码是反的,这儿处理下} else {code = "1" + code;}currNode = currNode.parent;}encodeMap.put(data.toString(), code); // 初始化编码表decodeMap.put(code, data.toString()); // 初始化解码表}}
}测试用例
public static void main(String[] args) {// a:3 b:24 c:6 d:20 e:34 f:4 g:12Map<Character, Integer> weights = new HashMap<Character, Integer>();weights.put('a', 3);weights.put('b', 24);weights.put('c', 6);weights.put('d', 20);weights.put('e', 34);weights.put('f', 4);weights.put('g', 12);HuffmenTree huffmenTree = new HuffmenTree(weights);huffmenTree.builder();huffmenTree.leafencode();huffmenTree.root.show();String input = "aceg";String encode = huffmenTree.encode(input);String decode = huffmenTree.decode(encode);String log = String.format("编码表:%s\n解码表:%s\n输入:%s\n编码结果:%s\n解码结果:%s",huffmenTree.encodeMap,huffmenTree.decodeMap,input,encode,decode);System.out.println(log);}
运行结果
null / \ null null / \ / \ d b null e / \ g null / \ c null / \ a f
编码表:{a=10110, b=01, c=1010, d=00, e=11, f=10111, g=100}
解码表:{00=d, 11=e, 01=b, 100=g, 10110=a, 1010=c, 10111=f}
输入:aceg
编码结果:10110101011100
解码结果:acega f
编码表:{a=10110, b=01, c=1010, d=00, e=11, f=10111, g=100}
解码表:{00=d, 11=e, 01=b, 100=g, 10110=a, 1010=c, 10111=f}
输入:aceg
编码结果:10110101011100
解码结果:aceg