1. 阶乘的概念

公式：$n!={\prod }_{k=1}^{n}k,\forall n\ge 1.$

2. 方法1：循环

# method 1. 
def factorial_1(n):if n<1:return 1res = 1for i in range(1, n+1):res *= ireturn res

测试：

prod_n = factorial_1(6)
print("prod", prod_n)#720

这里，也可以使用reduce来实现for循环，reduce() 函数会对参数序列中元素进行累积。
reduce() 函数的语法是：

reduce(function, iterable[,initalizer])

实现阶乘：

# method 2.
from functools import reduce
def factorial_2(n):if n<1:return 1res = reduce(lambda x,y:x*y, range(1,n+1))return res

3. 方法2：递归

循环的写法可以用递归来实现。

def factorial_3(n):if n == 0 or n == 1:return 1return factorial_3(n-1)*n

4. 方法3：math包实现

# method 4. math 
import math 
def factorial_4(n):res = math.factorial(n)return res

在python3中math包实用了分治算法，公式为：

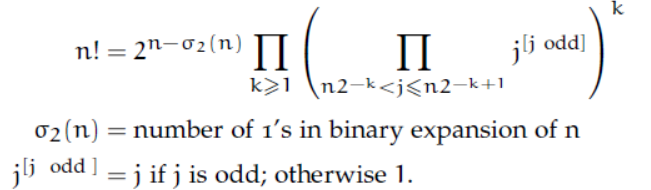
具体的实现是：

# A pure Python version.# Returns the number of bits necessary to represent an integer in binary, 
# excluding the sign and leading zeros.
# Needed only for Python version < 3.0; otherwise use n.bit_length().
def bit_length(self):s = bin(self)       # binary representation:  bin(-37) --> '-0b100101's = s.lstrip('-0b') # remove leading zeros and minus signreturn len(s)       # len('100101') --> 6def num_of_set_bits(i) :# assert 0 <= i < 0x100000000i = i - ((i >> 1) & 0x55555555)i = (i & 0x33333333) + ((i >> 2) & 0x33333333)return (((i + (i >> 4) & 0xF0F0F0F) * 0x1010101) & 0xffffffff) >> 24def rec_product(start, stop):"""Product of integers in range(start, stop, 2), computed recursively.start and stop should both be odd, with start <= stop."""numfactors = (stop - start) >> 1if numfactors == 2 : return start * (start + 2)if numfactors > 1 :mid = (start + numfactors) | 1return rec_product(start, mid) * rec_product(mid, stop)if numfactors == 1 : return startreturn 1def binsplit_factorial(n):"""Factorial of nonnegative integer n, via binary split."""inner = outer = 1for i in range(n.bit_length(), -1, -1):inner *= rec_product((n >> i + 1) + 1 | 1, (n >> i) + 1 | 1)outer *= innerreturn outer << (n - num_of_set_bits(n))# Test (from math import factorial).
[[n, binsplit_factorial(n) - factorial(n)] for n in range(99)]

---

参考：

1. binarysplitfact;
2. github factorial;
3. why-is-math-factorial-much-slower-in-python-2-x-than-3-x