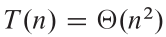问题:若某算法的计算时间表示为递推关系式:T(N)=2T(N/2)+NlogN 且 T(1)=1
则该算法的时间复杂度为( )。
O(Nsqrt(N))
O(NlogN)
O(N(logN)^2)
O(N^2logN)
O(N^2)
解析:
应该是 O(N(logN)^2)
参考网址:主定理和《算法导论》

但是博主说其实你不会主定理也没事儿,只要能找几个特殊值带入,并根据符号O的意义排除选项即可。所以……其实可以投机取巧。(望天)
主定理在《算法导论》的第53页时间复杂度章节有讲到(是的,黑色的很厚的那本)

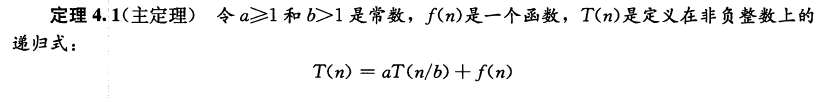

对于三种情况的每一种,我们将函数f(n)与函数 n l o g b a n^{log_ba} nlogba进行比较。 直觉上, 两个函数较大者决定了递归式的解。若函数 n l o g b a n^{log_ba} nlogba更大,如情况1,则解为 T ( n ) = Θ ( n l o g b a ) T(n)=Θ(n^{log_ba}) T(n)=Θ(nlogba)。若函数f(n)更大,如情况3,则解为 T ( n ) = Θ ( f ( n ) ) T(n)=Θ(f(n)) T(n)=Θ(f(n))。若两个函数大小相当, 如情况2,则乘上一个对数因子,解为 T ( n ) = Θ ( n l o g b a l g n ) = Θ ( f ( n ) l g n ) 。 T(n)= Θ(n^{log_ba}lgn) = Θ(f(n)lgn)。 T(n)=Θ(nlogbalgn)=Θ(f(n)lgn)。
注意, 这三种情况并未覆盖f(n)的所有可能性。情况1和情况2之间有一定间隙,f(n)可能小于 n l o g b a n^{log_ba} nlogba但不是多项式意义上的小于。 类似地,情况2和情况3之间也有一定间隙 ,f(n)可能大于 n l o g b a n^{log_ba} nlogba.但不是多项式意义上的大于。如果函数f(n)落在这两个间隙中,或者情况3中要求的正则条件不成立,就不能使用主方法来求解递归式。
在第一种情况中,不是 f(n)小于 n l o g b a n^{log_ba} nlogba就够了,
而是要多项式意义上的小于。 也就是说,f(n)必须渐近小于 n l o g b a n^{log_ba} nlogba,要相差一个因子 n ϵ n^ϵ nϵ,其中ϵ是大于0的常数。 在第三种情况中,不是f(n)大于 n l o g b a n^{log_ba} nlogba就够了,而是要多项式意义上的大于,而且还要满足“正则”条件 a f ( n / b ) ≤ c f ( n ) af(n/b)\leq cf(n) af(n/b)≤cf(n)。我们将会遇到的多项式界的函数中, 多数都满足此条件。
假设我们有递推关系式:

根据这个题, T ( N ) = 2 T ( N / 2 ) + N l o g N 且 T ( 1 ) = 1 , T(N)=2T(N/2)+NlogN 且 T(1)=1, T(N)=2T(N/2)+NlogN且T(1)=1,可知 a = 2 , b = 2 , f ( n ) = N l o g N , a=2,b=2,f(n)=NlogN, a=2,b=2,f(n)=NlogN,所以将函数 f ( n ) = N l o g N f(n)=NlogN f(n)=NlogN与函数 N l o g 2 2 l o g N = N l o g N N^{log_22}logN=NlogN Nlog22logN=NlogN进行比较,他们复杂度相近,是情况2。从而根据公式:
f ( n ) = Θ ( n l o g b a l o g k n ) , 则 T ( n ) = Θ ( n l o g b a l o g k + 1 n ) 。 f(n)=Θ(n^{log_ba}log_kn) ,则T(n)=Θ(n^{log_ba}log^{k+1}n)。 f(n)=Θ(nlogbalogkn),则T(n)=Θ(nlogbalogk+1n)。
有:
Γ ( n ) = n l o g 2 2 ∗ ( l o g 2 n ) = n ( l o g n ) 2 \Gamma(n) = n^{log_22}*(log^2n)\,= n(logn)^2 Γ(n)=nlog22∗(log2n)=n(logn)2
类题试解:
1.二叉树的遍历: T ( n ) = 2 T ( n 2 ) + Θ ( 1 ) T(n)=2T(\frac{n}{2})+Θ(1) T(n)=2T(2n)+Θ(1)
可知 a = 2 , b = 2 , f ( n ) = 1 a=2,b=2,f(n)=1 a=2,b=2,f(n)=1, n l o g 2 2 = n n^{log_22}=n nlog22=n比 f ( n ) = Θ ( 1 ) f(n)=Θ(1) f(n)=Θ(1)大,是情况1,则根据公式,解为 T ( n ) = Θ ( n l o g 2 2 ) = Θ ( n ) T(n)=Θ(n^{log_22})=Θ(n) T(n)=Θ(nlog22)=Θ(n)
2.二分搜索(折半搜索) T ( n ) = T ( n 2 ) + Θ ( 1 ) T(n)=T(\frac{n}{2})+Θ(1) T(n)=T(2n)+Θ(1)
可知a=1,b=2,f(n)=Θ(1),
n l o g 2 1 = n 0 = 1 n^{log_21}=n^0=1 nlog21=n0=1,故f(n)和O(1)复杂度相近,是情况2,
根据公式, T ( n ) = l g n T(n)=lgn T(n)=lgn
3.最大子数组问题和归并排序的分治算法的运行时间: T ( n ) = 2 T ( n 2 ) + Θ ( n ) T(n)=2T(\frac{n}{2})+Θ(n) T(n)=2T(2n)+Θ(n)
可知a=2,b=2, f ( n ) = Θ ( n ) f(n)=Θ(n) f(n)=Θ(n)
n l o g 2 2 = n n^{log_22}=n nlog22=n和 f ( n ) = Θ ( n ) f(n)=Θ(n) f(n)=Θ(n)相近,是情况2,
根据公式, T ( n ) = Θ ( n l o g b a l g n ) = Θ ( f ( n ) l g n ) 。 T(n)= Θ(n^{log_ba}lgn) = Θ(f(n)lgn)。 T(n)=Θ(nlogbalgn)=Θ(f(n)lgn)。
可得 T ( n ) = Θ ( n l o g 2 2 l g n ) = Θ ( n l o g 2 n ) 。 T(n)= Θ(n^{log_22}lgn) = Θ(nlog_2n)。 T(n)=Θ(nlog22lgn)=Θ(nlog2n)。
4.递归式 T ( n ) = 3 T ( n / 4 ) + n l g n T(n) = 3T(n/4) +nlgn T(n)=3T(n/4)+nlgn
我们有 a = 3 , b = 4 , f ( n ) = n l g n a=3,b=4, f(n)=nlgn a=3,b=4,f(n)=nlgn,而 n l o g 4 3 = O ( n 0.793 ) n^{log_43}=O(n^{0.793}) nlog43=O(n0.793)
由于 f ( n ) = Ω ( n l o g 4 3 + ϵ ) = Ω ( n 0.793 + ϵ ) f(n)=\Omega(n^{log_43+ϵ})=\Omega(n^{0.793+ϵ}) f(n)=Ω(nlog43+ϵ)=Ω(n0.793+ϵ),其中 ϵ ≈ 1 − 0.793 = 0.2 ϵ\approx1-0.793=0.2 ϵ≈1−0.793=0.2, f ( n ) = n l g n > n l o g 4 3 f(n)=nlgn>n^{log_43} f(n)=nlgn>nlog43满足情况3。且对常数c=0.75和所有足够大的n有 3 ( n / 4 ) l g ( n / 4 ) ≤ 0.75 n l g n = c f ( n ) 3(n/4)lg(n/4)\leq 0.75nlgn=cf(n) 3(n/4)lg(n/4)≤0.75nlgn=cf(n)
故解为 T ( n ) = Θ ( n l g n ) T(n)= Θ(nlgn) T(n)=Θ(nlgn)
5.矩阵乘法问题第一个分治算法 T ( n ) = 8 T ( n 2 ) + Θ ( n 2 ) T(n)=8T(\frac{n}{2})+Θ(n^2) T(n)=8T(2n)+Θ(n2)
有 a = 8 , b = 2 , f ( n ) = n 2 a=8,b=2,f(n)=n^2 a=8,b=2,f(n)=n2, n l o g 2 8 = n 3 n^{log_28}=n^3 nlog28=n3可以看出 f ( n ) = n 2 < n 3 f(n)=n^2<n^3 f(n)=n2<n3,应该是情况1,其中 ϵ = 1 ϵ=1 ϵ=1
故 T ( n ) = Θ ( n 3 ) T(n)= Θ(n^3) T(n)=Θ(n3)
6.Strassen算法的运行时间 T ( n ) = 7 T ( n / 2 ) + Θ ( n 2 ) T(n) = 7T(n/2) +Θ(n^2) T(n)=7T(n/2)+Θ(n2)
有a=7,b=2, n l o g 2 7 ≈ n 2.805 > n 2 , 故 f ( n ) < n 2.805 n^{log_27}\approx n^{2.805}>n^2,故f(n)<n^{2.805} nlog27≈n2.805>n2,故f(n)<n2.805,应用情况1公式:
故 T ( n ) = Θ ( n l o g 2 7 ) T(n)= Θ(n^{log_27}) T(n)=Θ(nlog27)
改写底为 l g 7 lg7 lg7
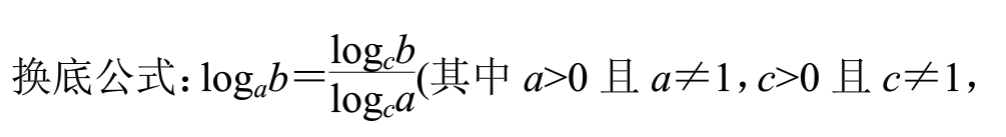
l o g 2 7 = l g 7 l g 2 = 0.84 0.3 = 2.807 log_27=\frac{lg7}{lg2}=\frac{0.84}{0.3}=2.807 log27=lg2lg7=0.30.84=2.807
算法导论中的lg以2为底
故 T ( n ) = Θ ( n l g 7 ) = Θ ( n 2.807 ) T(n)= Θ(n^{lg7})=Θ(n^{2.807}) T(n)=Θ(nlg7)=Θ(n2.807)
不能使用主定理的情况: T ( n ) = 2 T ( n / 2 ) + Θ ( n l g n ) T(n) = 2T(n/2) +Θ(nlgn) T(n)=2T(n/2)+Θ(nlgn)
其中 a = 2 , b = 2 , f ( n ) = n l g n a=2,b=2,f(n)=nlgn a=2,b=2,f(n)=nlgn
而 l o g 2 2 = n log_22=n log22=n 而 f ( n ) = n l g n f(n)=nlgn f(n)=nlgn渐进大于n,而不是多项式大于n
(多项式意义上的大于,顾名思义,就是两个函数的商大于一个多项式。严格表述为如下形式:当我们说f(x)多项式意义上大于g(x)时,我们是指:存在实数e>0,使得f(x)>g(x)*n^e。)
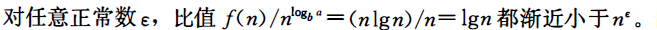
因此, 递归式落入了情况2和情况3之间的间隙,不可以使用主定理。
不过可以利用公式:
f ( n ) = Θ ( n l o g b a l o g k n ) , 则 T ( n ) = Θ ( n l o g b a l o g k + 1 n ) 。 f(n)=Θ(n^{log_ba}log_kn) ,则T(n)=Θ(n^{log_ba}log^{k+1}n)。 f(n)=Θ(nlogbalogkn),则T(n)=Θ(nlogbalogk+1n)。
根据算法导论P73的上下界取整:

可知 O ( N l o g 2 2 N ) O(Nlog^2_2N) O(Nlog22N)是T(n)的上界( O ( N 3 ) O(N^3) O(N3)也是上界,但是不是紧确界)