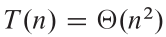分治法主定理

主定理的证明
假设有递归式:
T ( n ) = a T ( n b ) + f ( n ) T(n) = aT(\frac{n}{b}) + f(n) T(n)=aT(bn)+f(n)
证明:
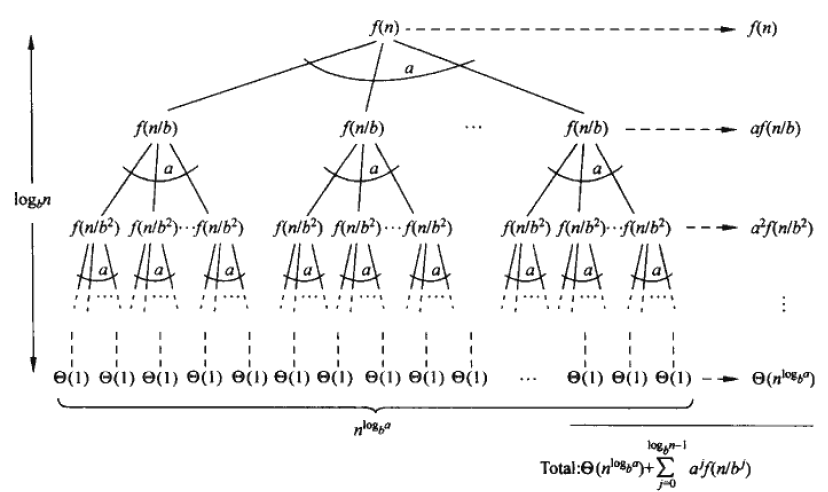
T ( n ) = a T ( n / b ) + f ( n ) T(n) = aT(n/b) + f(n) T(n)=aT(n/b)+f(n) = a [ a T ( n / b 2 ) + f ( n / b ) ] + f ( n ) = a\big[aT(n/b^2)+f(n/b)\big] + f(n) =a[aT(n/b2)+f(n/b)]+f(n) = a 2 T ( n / b 2 ) + f ( n ) + a f ( n / b ) = a^2T(n/b^2) + f(n) + af(n/b) ~\, =a2T(n/b2)+f(n)+af(n/b) = a k T ( n / b k ) + ∑ j = 0 k − 1 a j f ( n / b j ) = a^{k}T(n/b^k) + \sum_{j=0}^{k-1} a^j f(n/b^j) ~~~~ =akT(n/bk)+j=0∑k−1ajf(n/bj) = ⋯ ( 不 妨 设 n 是 b 的 幂 ) = \cdots ~(不妨设n是b的幂)~~~~~~~~~~~~ =⋯ (不妨设n是b的幂) = a l o g b n T ( 1 ) + ∑ j = 0 l o g b n − 1 a j f ( n / b j ) = a^{log_b^n}T(1) + \sum_{j=0}^{log_b^n-1} a^j f(n/b^j) ~~ =alogbnT(1)+j=0∑logbn−1ajf(n/bj)
由对数的换底公式: a l o g b n = b l o g b ( a l o g b n ) = b l o g b a l o g b n = b l o g b n l o g b a = b l o g b ( n l o g b a ) = n l o g b a a^{log_b^n} =b^{log_b^{(a^{log_b^n})}} =b^{log_b^a log_b^n} =b^{log_b^n log_b^a}= b^{log_b^{(n^{log_b^a})}}=n^{log_b^a} alogbn=blogb(alogbn)=blogbalogbn=blogbnlogba=blogb(nlogba)=nlogba
所以原递归式的渐进复杂度为 O ( n l o g b a ) + ∑ j = 0 l o g b n − 1 a j f ( n / b j ) O(n^{log_b^a}) + \sum_{j=0}^{log_b^n-1} a^j f(n/b^j) O(nlogba)+j=0∑logbn−1ajf(n/bj)
简单起见,下面只考虑 f ( n ) = n k f(n) = n^k f(n)=nk 的情形:
∑ j = 0 l o g b n − 1 a j f ( n / b j ) \sum_{j=0}^{log_b^n-1} a^j f(n/b^j) j=0∑logbn−1ajf(n/bj) = ∑ j = 0 l o g b n − 1 a j ( n / b j ) k = \sum_{j=0}^{log_b^n-1} a^j (n/b^j)^k ~~~~~~~ =j=0∑logbn−1aj(n/bj)k = n k ∑ j = 0 l o g b n − 1 ( a / b k ) j = n^k\sum_{j=0}^{log_b^n-1} (a/b^k)^j ~~~~~~~ =nkj=0∑logbn−1(a/bk)j = { n k ( 1 − ( a / b k ) l o g b n 1 − a / b k ) , 如果 a ≠ b k n k ( l o g b n − 1 ) , 如果 a = b k = \left\{ \begin{array}{lr} n^k \left(\frac{1-(a/b^k)^{log_b^n}}{1-a/b^k}\right), & \text{如果$a\neq b^k$}\\ &\\ n^k(log_b^n-1), & \text{如果$a = b^k$} \end{array} \right. =⎩⎪⎨⎪⎧nk(1−a/bk1−(a/bk)logbn),nk(logbn−1),如果a=bk如果a=bk = { O ( n k ) , 如果 a < b k ( k > l o g b a ) O ( n l o g b a ) , 如果 a > b k O ( n k l o g b n ) = O ( n l o g b a l o g b n ) , 如果 a = b k = \left\{ \begin{array}{lr} O(n^k) , & \text{如果$a < b^k(k>log_b^a)$}\\ &\\ O(n^{log_b^a}), & \text{如果$a> b^k$}\\ &\\ O(n^klog_b^n)=O(n^{log_b^a}log_b^n), & \text{如果$a = b^k$} \end{array} \right. =⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧O(nk),O(nlogba),O(nklogbn)=O(nlogbalogbn),如果a<bk(k>logba)如果a>bk如果a=bk
综上所述,对 T ( n ) = a T ( n b ) + f ( n ) T(n) = aT(\frac{n}{b}) + f(n) T(n)=aT(bn)+f(n) 的情形:
T ( n ) = { O ( n k ) , 如果 a < b k ( k > l o g b a ) O ( n l o g b a ) , 如果 a > b k O ( n k l o g b n ) = O ( n l o g b a l o g b n ) , 如果 a = b k T(n)= \left\{ \begin{array}{lr} O(n^k) , & \text{如果$a< b^k(k>log_b^a)$}\\ &\\ O(n^{log_b^a}), & \text{如果$a> b^k$}\\ &\\ O(n^klog_b^n)=O(n^{log_b^a}log_b^n), & \text{如果$a = b^k$} \end{array} \right. T(n)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧O(nk),O(nlogba),O(nklogbn)=O(nlogbalogbn),如果a<bk(k>logba)如果a>bk如果a=bk
减治法主定理