高斯拉普拉斯算子(Laplacian of Gaussian,LoG)
高斯拉普拉斯算子(Laplacian of Gaussian,LoG)提取图像 f ( x , y ) f(x, y) f(x,y)边缘:
- 图像平滑去噪,高斯低通滤波器(a convolution with a Gaussian kernel of width σ \sigma σ)
G σ ( x , y ) = 1 2 π σ exp ( − x 2 + y 2 2 σ 2 ) G_{\sigma}(x, y) = \frac{1}{\sqrt{2 \pi} \sigma} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) Gσ(x,y)=2πσ1exp(−2σ2x2+y2)
- 边缘检测,拉普拉斯算子(Laplace operator)
△ ( G σ ( x , y ) ∗ f ( x , y ) ) = ( △ G σ ( x , y ) ) ∗ f ( x , y ) = LoG ∗ f ( x , y ) \bigtriangleup (G_{\sigma}(x, y) * f(x, y)) = (\bigtriangleup G_{\sigma}(x, y)) * f(x, y) = \text{LoG} * f(x, y) △(Gσ(x,y)∗f(x,y))=(△Gσ(x,y))∗f(x,y)=LoG∗f(x,y)
■■
卷积性质:
d d t ( h ( t ) ∗ f ( t ) ) = d d t ∫ f ( τ ) h ( t − τ ) d τ = ∫ f ( τ ) d d t h ( t − τ ) d τ = f ( t ) ∗ d d t h ( t ) \frac{d}{dt} (h(t) * f(t)) = \frac{d}{dt} \int f(\tau) h(t - \tau) d \tau = \int f(\tau) \frac{d}{dt} h(t - \tau) d \tau = f(t) * \frac{d}{dt} h(t) dtd(h(t)∗f(t))=dtd∫f(τ)h(t−τ)dτ=∫f(τ)dtdh(t−τ)dτ=f(t)∗dtdh(t)
■
高斯拉普拉斯算子 △ G σ ( x , y ) \bigtriangleup G_{\sigma}(x,y) △Gσ(x,y):
∂ 2 ∂ x 2 G σ ( x , y ) = 1 2 π σ x 2 − σ 2 σ 4 exp ( − x 2 + y 2 2 σ 2 ) \frac{\partial^{2}}{\partial x^{2}} G_{\sigma}(x, y) = \frac{1}{\sqrt{2 \pi} \sigma} \frac{x^{2} - \sigma^{2}}{\sigma^{4}} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) ∂x2∂2Gσ(x,y)=2πσ1σ4x2−σ2exp(−2σ2x2+y2)
∂ 2 ∂ y 2 G σ ( x , y ) = 1 2 π σ y 2 − σ 2 σ 4 exp ( − x 2 + y 2 2 σ 2 ) \frac{\partial^{2}}{\partial y^{2}} G_{\sigma}(x, y) = \frac{1}{\sqrt{2 \pi} \sigma} \frac{y^{2} - \sigma^{2}}{\sigma^{4}} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) ∂y2∂2Gσ(x,y)=2πσ1σ4y2−σ2exp(−2σ2x2+y2)
■■
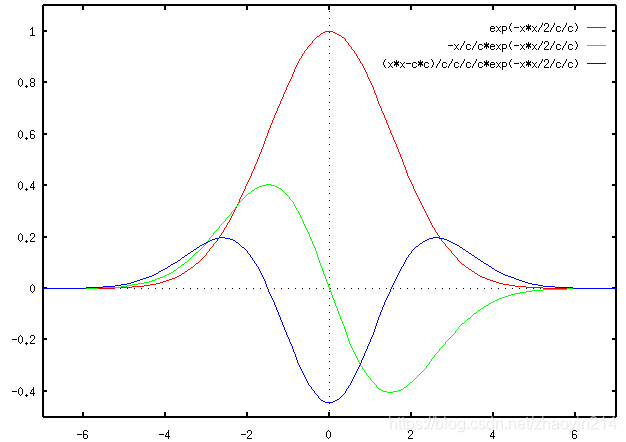
∂ ∂ x G σ ( x , y ) = 1 2 π σ ∂ ∂ x exp ( − x 2 + y 2 2 σ 2 ) = − x 2 π σ 3 exp ( − x 2 + y 2 2 σ 2 ) \frac{\partial}{\partial x} G_{\sigma}(x, y) = \frac{1}{\sqrt{2 \pi} \sigma} \frac{\partial }{\partial x} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) = - \frac{x}{\sqrt{2 \pi} \sigma^{3}} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) ∂x∂Gσ(x,y)=2πσ1∂x∂exp(−2σ2x2+y2)=−2πσ3xexp(−2σ2x2+y2)
∂ 2 ∂ x 2 G σ ( x , y ) = − 1 2 π σ 3 exp ( − x 2 + y 2 2 σ 2 ) + x 2 2 π σ 5 exp ( − x 2 + y 2 2 σ 2 ) = 1 2 π σ x 2 − σ 2 σ 4 exp ( − x 2 + y 2 2 σ 2 ) \frac{\partial^{2}}{\partial x^{2}} G_{\sigma}(x, y) = - \frac{1}{\sqrt{2 \pi} \sigma^{3}} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) + \frac{x^{2}}{\sqrt{2 \pi} \sigma^{5}} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) = \frac{1}{\sqrt{2 \pi} \sigma} \frac{x^{2} - \sigma^{2}}{\sigma^{4}} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) ∂x2∂2Gσ(x,y)=−2πσ31exp(−2σ2x2+y2)+2πσ5x2exp(−2σ2x2+y2)=2πσ1σ4x2−σ2exp(−2σ2x2+y2)
■
LoG \text{LoG} LoG定义为:
LoG ≜ ∂ 2 ∂ x 2 G σ ( x , y ) + ∂ 2 ∂ y 2 G σ ( x , y ) = 1 2 π σ x 2 + y 2 − 2 σ 2 σ 4 exp ( − x 2 + y 2 2 σ 2 ) \text{LoG} \triangleq \frac{\partial^{2}}{\partial x^{2}} G_{\sigma}(x, y) + \frac{\partial^{2}}{\partial y^{2}} G_{\sigma}(x, y) = \frac{1}{\sqrt{2 \pi} \sigma} \frac{x^{2} + y^{2} - 2 \sigma^{2}}{\sigma^{4}} \exp \left( - \frac{x^{2} + y^{2}}{2 \sigma^{2}} \right) LoG≜∂x2∂2Gσ(x,y)+∂y2∂2Gσ(x,y)=2πσ1σ4x2+y2−2σ2exp(−2σ2x2+y2)
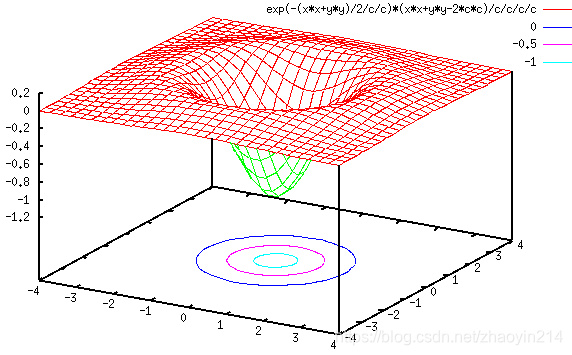
二维 5 × 5 5 \times 5 5×5 LoG \text{LoG} LoG算子:
[ 0 0 1 0 0 0 1 2 1 0 1 2 − 16 2 1 0 1 2 1 0 0 0 1 0 0 ] \begin{bmatrix} 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 2 & 1 & 0 \\ 1 & 2 & -16 & 2 & 1 \\ 0 & 1 & 2 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ \end{bmatrix} ⎣⎢⎢⎢⎢⎡001000121012−16210121000100⎦⎥⎥⎥⎥⎤
核矩阵各元素之和必须为零(make sure that the sum (or average) of all elements of the kernel has to be zero)。
边缘检测步骤:
-
LoG滤波(applying LoG to the image)
-
过零检测(detection of zero-crossings in the image)
-
门限判决(threshold the zero-crossings to keep only those strong ones (large difference between the positive maximum and the negative minimum))