外连接(out join)
外连接分为外左连接(left outer join)和外右连接(right outer join)
注释:left outer join 与 left join 等价, 一般写成left join
right outer join 与 right join等价,一般写成right join
左连接,取左边的表的全部,右边的表按条件,符合的显示,不符合则显示null
举例:select <select list> from A left join B on A.id=B.id

右连接:取右边的表的全部,左边的表按条件,符合的显示,不符合则显示null
举例:select <select list> from A right join B on A.id=B.id

内连接(inner join)
内连接:也称为等值连接,返回两张表都满足条件的部分
注释:inner join 就等于 join
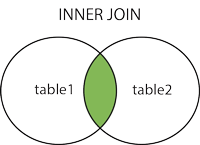
交叉连接(CROSS JOIN)
交叉连接:返回左表中的所有行,左表中的每一行与右表中的所有行组合。交叉联接也称作笛卡尔积
首先,先简单解释一下笛卡尔积:笛卡尔乘积是指在数学中,两个集合X和Y的笛卡尓积(Cartesian product),又称直积,表示为X × Y,第一个对象是X的成员而第二个对象是Y的所有可能有序对的其中一个成员
举例:
现在,我们有两个集合A和B。
A = {0,1} B = {2,3,4}
集合 A×B 和 B×A的结果集就可以分别表示为以下这种形式:
A×B = {(0,2),(1,2),(0,3),(1,3),(0,4),(1,4)};
B×A = {(2,0),(2,1),(3,0),(3,1),(4,0),(4,1)};
以上A×B和B×A的结果就可以叫做两个集合相乘的‘笛卡尔积’。
从以上的数据分析我们可以得出以下两点结论:
1,两个集合相乘,不满足交换率,既 A×B ≠ B×A;
2,A集合和B集合相乘,包含了集合A中元素和集合B中元素相结合的所有的可能性。既两个集合相乘得到的新集合的元素个数是 A集合的元素个数 × B集合的元素个数;
交叉连接有两种,显式的和隐式的,不带ON子句,返回的是两表的乘积,也叫笛卡尔积。
例如:下面的语句1和语句2的结果是相同的。
语句1:隐式的交叉连接,没有CROSS JOIN。
SELECT O.ID, O.ORDER_NUMBER, C.ID, C.NAME
FROM ORDERS O , CUSTOMERS C
WHERE O.ID=1;
语句2:显式的交叉连接,使用CROSS JOIN。
SELECT O.ID,O.ORDER_NUMBER,C.ID,
C.NAME
FROM ORDERS O CROSS JOIN CUSTOMERS C
WHERE O.ID=1;
内连接和where的区别:
数据库表连接数据行匹配时所遵循的算法就是以上提到的笛卡尔积,表与表之间的连接可以看成是在做乘法运算。
比如现在数据库中有两张表,student表和 student_subject表,如下所示:
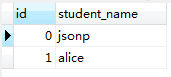
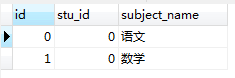
我们执行以下的sql语句,只是纯粹的进行表连接。
SELECT * from student JOIN student_subject; SELECT * from student_subject JOIN student;
看一下执行结果:
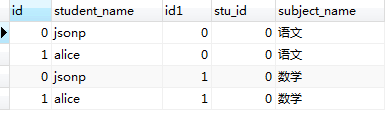
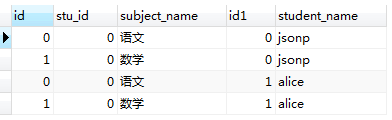
表1.0 表1.1
从执行结果上来看,结果符合我们以上提出的两点结论(红线标注部分);
以第一条sql语句为例我们来看一下他的执行流程,
1,from语句把student表 和 student_subject表从数据库文件加载到内存中。
2,join语句相当于对两张表做了乘法运算,把student表中的每一行记录按照顺序和student_subject表中记录依次匹配。
3,匹配完成后,我们得到了一张有 (student中记录数 × student_subject表中记录数)条的临时表。 在内存中形成的临时表如表1.0所示。我们又把内存中表1.0所示的表称为‘笛卡尔积表’。
再看一下sql中主要关键字的执行顺序:
from
on
join
where
group by
having
select
distinct
union
order by
我们看到on是在join和where前面的
如果两张表的数据量都比较大的话,那样就会占用很大的内存空间这显然是不合理的。所以,我们在进行表连接查询的时候一般都会使用JOIN xxx ON xxx的语法,ON语句的执行是在JOIN语句之前的,也就是说两张表数据行之间进行匹配的时候,会先判断数据行是否符合ON语句后面的条件,再决定是否JOIN。
因此,有一个显而易见的SQL优化的方案是,当两张表的数据量比较大,又需要连接查询时,应该使用 FROM table1 JOIN table2 ON xxx的语法,避免使用 FROM table1,table2 WHERE xxx 的语法,因为后者会在内存中先生成一张数据量比较大的笛卡尔积表,增加了内存的开销。
全连接(Full join)
全外连接是在结果中除了显示满足连接的条件的行外,还显示了join两侧表中所有满足检索条件的行