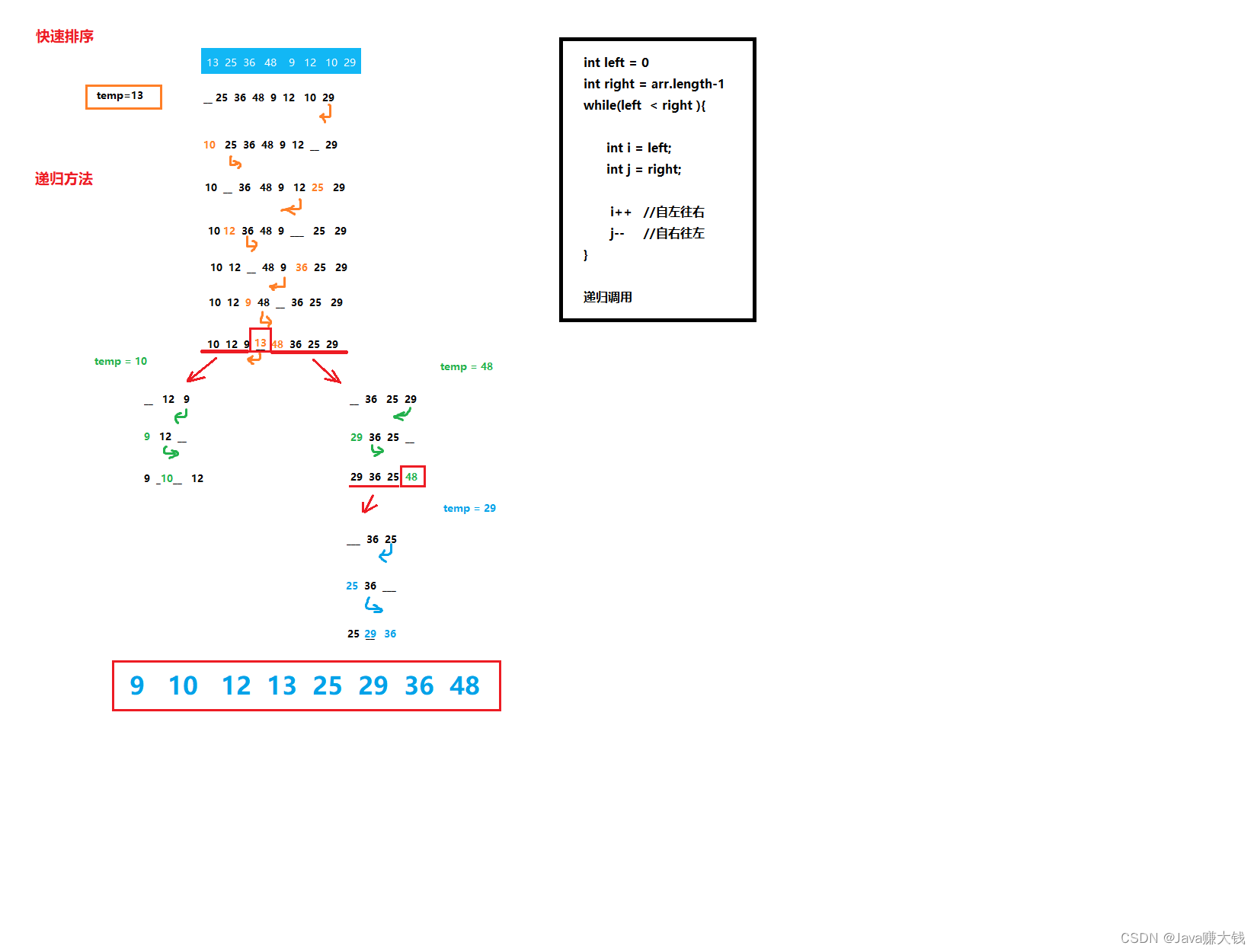
快速排序的思想是用数组的首元素作为标准将A划分成前后两部分，比首元素小的元素构成数组的前部分，比首元素大的元素构成数组的后部分，这两部分构成两个新的子问题，算法接着分别对这两部分递归进行排序

---

伪代码：

输入：数组，      //p,r分别为数组A的首元素和尾元素的下标

输出：从到按照递增顺序排好序的数组A

1. if p<r
2. then      //划分数组，找到首元素在排好序后的位置q
3.       
4.       
5.       

C语言代码如下：

void QuickSort(int *A, int p, int r)
{if (p < r){//数组分块int pivot = Partition(A,p,r); // 递归调用QuickSort(A, p, pivot - 1);     // 左边的继续快排 QuickSort(A, pivot + 1, r);    // 右边的继续快排 }
}

的过程为，先从后向前扫描数组A，找到第一个不大于的元素，然后从前扫描A找到第一个不大于的元素，当时，交换与。这时 后面的数都大于  ，前面的数都小于 ，重复上述操作，直到与相遇。当,就代表了在排好序的数组中的正确位置q。此时在q位置之前的元素都不大于，在q位置之后的元素都大于。根据上述过程，可以将原问题划成以q为边界的两个需要排序的子问题。

图示如下：

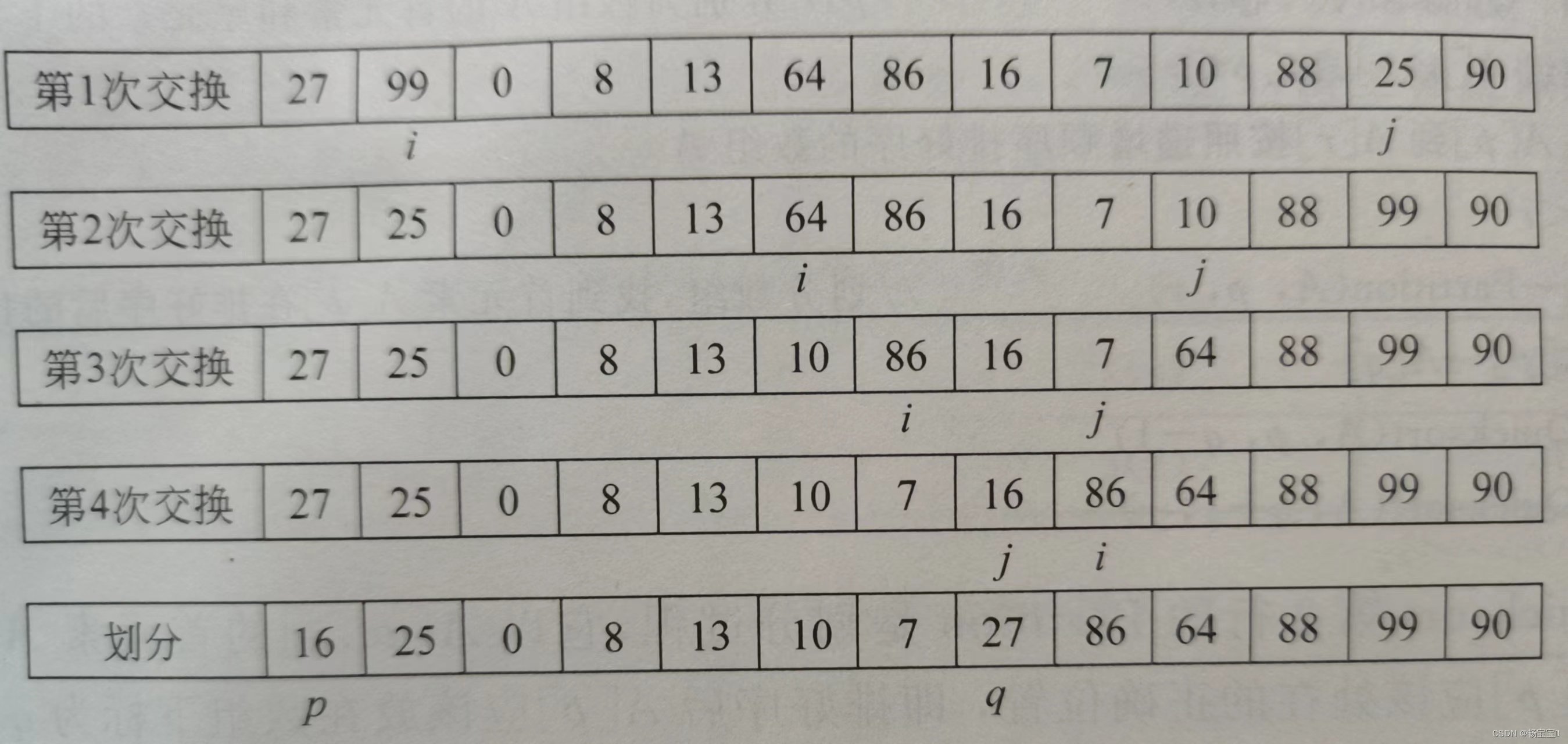
Partition（）伪代码为：

输入：数组

输出：j，A的首元素在排好序的数组中的位置

1. 
2. 
3. 
4. 
5.           
6.           
7.           
8.           
9.           
10. 
11. 

 C语言代码实现：

int Partition(int *A,int p,int r)
{int i = p;int j = r;int k = A[p];while (i < j){while(i < j && A[j] >= k)     // 从右向左找第一个小于k的数{j--;}A[i]=A[j];while(i < j && A[i] <= k)      // 从左向右找第一个大于等于k的数{i++;}A[j]=A[i];}A[i] = k;return i;} 

如果每次划分得到的子问题大小都相等，那么以上算法的时间复杂度的地推公式为：

该方程的解是

完整代码为：

//算法2.5 Quicksort(A,p,r)  //p,r分别为数组A的首元素和尾元素的下标 
//输入：数组A[p..r]，1<=p<=r<=n 
//输出：从A[p]到A[r]按照递增顺序排好序的数组A
#include<stdio.h>
#include<stdlib.h>void show(int array[], int len)
{int i;for(i = 0; i < len; i++){printf("%-3d", array[i]);}printf("\n");return ;
}void QuickSort(int *A, int p, int r)
{if (p < r){//数组分块int pivot = Partition(A,p,r); // 递归调用QuickSort(A, p, pivot - 1);     // 左边的继续快排 QuickSort(A, pivot + 1, r);    // 右边的继续快排 }
}int Partition(int *A,int p,int r)
{int i = p;int j = r;int k = A[p];while (i < j){while(i < j && A[j] >= k)     // 从右向左找第一个小于k的数{j--;}A[i]=A[j];while(i < j && A[i] <= k)      // 从左向右找第一个大于等于k的数{i++;}A[j]=A[i];}A[i] = k;return i;} 
int main()
{int A[13] = {27,99,0,8,13,64,86,16,7,10,88,25,90};int len = 13;printf("排序前:\n");show(A, len);QuickSort(A, 0, len-1);  // 快速排序printf("排序后:\n");show(A, len);return 0;
}

运行结果为：