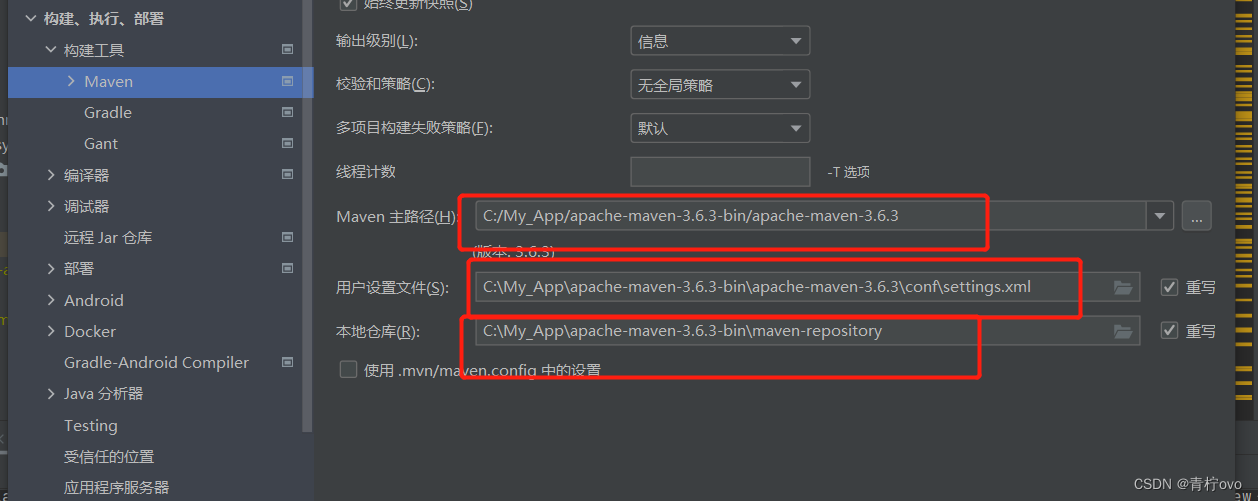
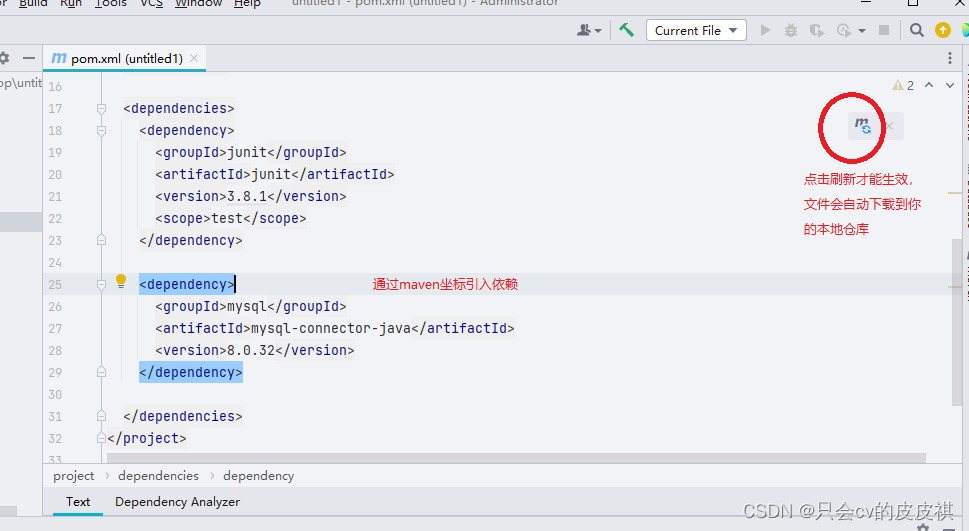
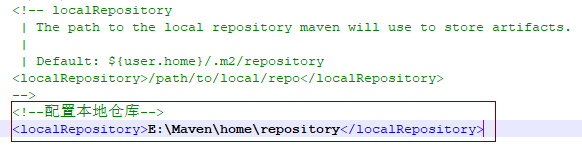
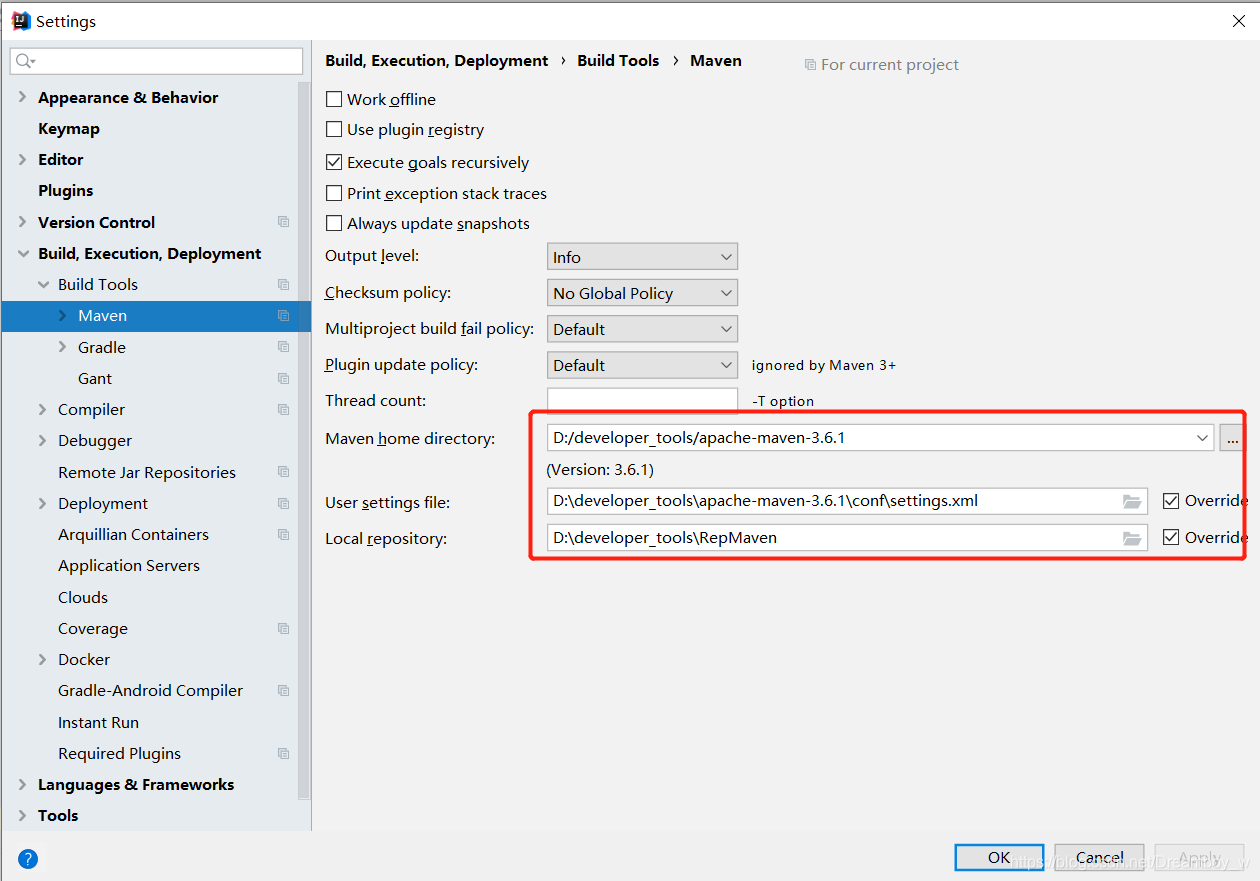
文章目录
- 前言
- 一、用二维数组实现杨辉三角
- 二、用一维数组实现杨辉三角
- 1.用两个一维数组实现杨辉三角
- 2.用一个一维数组实现杨辉三角
- 三、不用数组实现杨辉三角
- 总结
前言
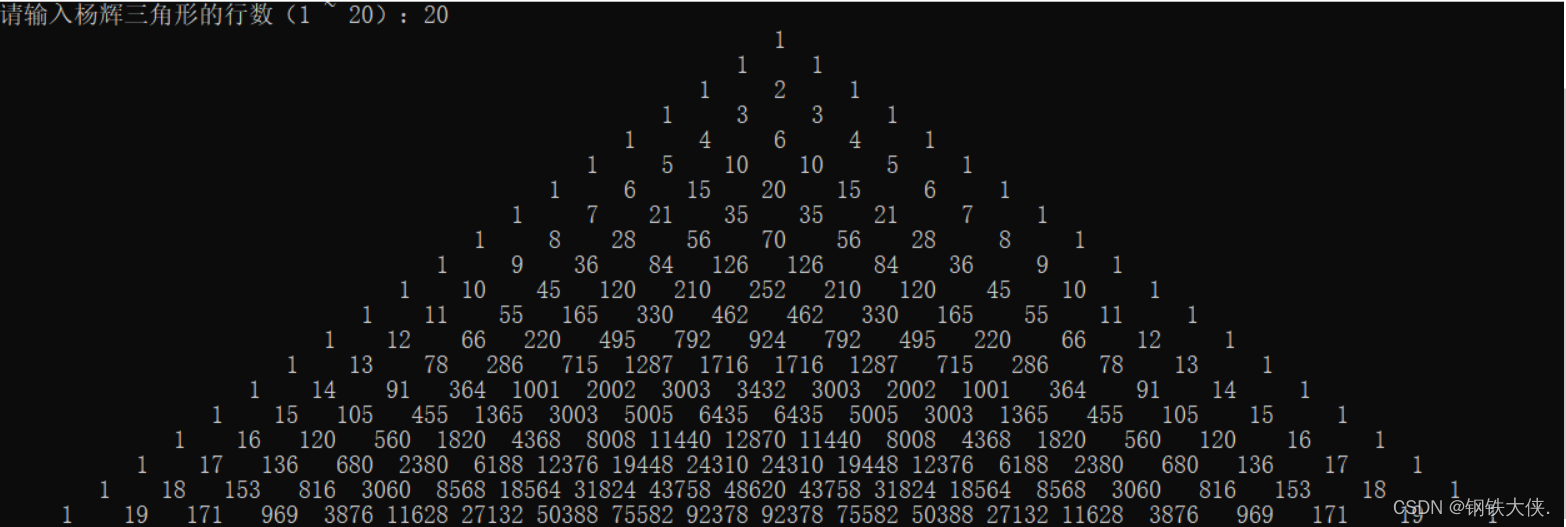
杨辉三角,是二项式系数在三角形中的一种几何排列。如下图所示,
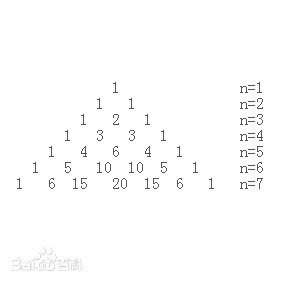
杨辉三角是中国古代数学的杰出研究成果之一,它把二项式系数图形化,把组合数内在的一些代数性质直观地从图形中体现出来,是一种离散型的数与形的结合。
本文将通过以下几个方面来实现杨辉三角:
1.用二维数组实现杨辉三角;
2.用一维数组实现杨辉三角;
2.1用两个一维数组实现杨辉三角;
2.2用一个一维数组实现杨辉三角;
3.不使用数组实现杨辉三角(使用for循环实现)
一、用二维数组实现杨辉三角
使用二维数组实现杨辉三角,也就是说,将杨辉三角看成是二维数组,有对应的行数和列数,例如,第1行第1列代表数1,第5行第2列代表4,如下图所示。

这里我们使用动态内存去申请二维数组,而二维数组可以看作是竖向的指针数组去指向横向的一维数组:
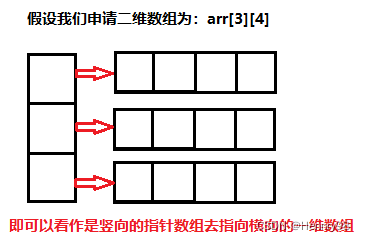
具体的实现过程如下代码所示:
void YangHui2(const int n) //利用二维数组去实现杨辉三角
{//二维数组可以看作是竖向的指针数组去指向横向的一维数组int** p = (int**)malloc(n * sizeof(int*)); //先申请竖的指针for (int i = 0; i < n; i++) //再用竖的指针去指向横向的数组{p[i] = (int*)malloc(n * sizeof(int));}assert(p != NULL); //断言for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){//特殊处理,防止数组越界if (j == 0 || i == j) //每一行的第一个值和最后一个值均为1{p[i][j] = 1;}else //其他的均是公式:当前值 = 上一行本列的值 + 上一行上一列的值{p[i][j] = p[i - 1][j] + p[i - 1][j - 1]; //此处不需要考虑数组越界问题,因为越界问题已经特殊处理}}}for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){printf("%-5d", p[i][j]); //打印杨辉三角}printf("\n");}for (int i = 0; i < n; i++){free(p[i]);//用malloc,一定要释放}free(p); //利用malloc后,释放指针p
}
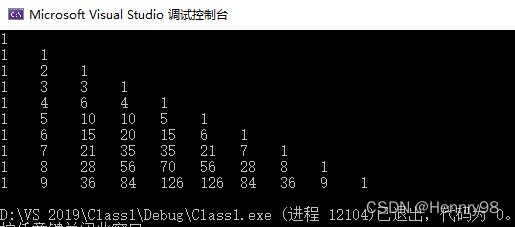
这里打印10行杨辉三角,运行结果如下:(如果想要打印等腰三角形形式的,可自行细调输出格式,这里对格式不作要求)

二、用一维数组实现杨辉三角
1.用两个一维数组实现杨辉三角
此过程利用两个一维数组arr[]和brr[],利用一个数组arr[]按照杨辉三角的规律进行下一行的计算,计算的值保存在另一个数组brr[]中,最后再将brr[]的值赋给数组arr[],打印arr[]即可。
注意一点的就是初始将数组arr[]和brr[]的值全部赋值为1,这样方便计算。
具体的实现过程如下代码所示:
void YangHui1_2(const int n) //一维数组实现杨辉三角(用两个一维数组)
{int* arr = (int*)malloc(n * sizeof(int));int* brr = (int*)malloc(n * sizeof(int)); //申请brr是为了存放arr中计算的值,最后再将值赋给arr即可assert(arr != NULL && brr != NULL); //断言指针不为空for (int i = 0; i < n; i++) //将arr和brr的值全部赋值为1{arr[i] = 1; //将数组arr的值全部赋为1,是为了便于对数组进行操作brr[i] = 1; //将数组brr的值全部赋为1,是为了便于对数组进行操作}for (int i = 0; i < n; i++) //外层循环处理第i行的数据{//这里内层j是从1开始,也就是第一列(j==0)不需要处理,因为都是1for (int j = 1; j < i; j++) //内部循环处理每一层的数据{//这里不需要考虑数组越界问题,由于列数j是从第2列开始的,所以不存在越界问题//利用公式不会超出第一列,最多到第一列,也就是brr[1] = arr[1] + arr[0];brr[j] = arr[j] + arr[j - 1]; //利用公式处理完每一层的数据,存放在brr中}//以下利用for循环将brr的值重新赋给arr,并打印arrfor (int k = 0; k <= i; k++){arr[k] = brr[k]; //将计算的值再重新赋给arrprintf("%-5d", arr[k]); //打印arr}printf("\n");}free(arr); //利用malloc后,要进行释放free(brr);
}
这里打印10行杨辉三角,运行结果如下:
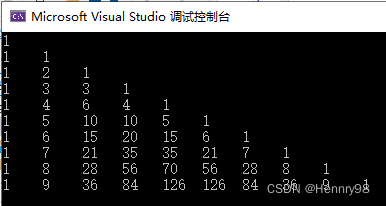
2.用一个一维数组实现杨辉三角
利用一个一维数组,此方法是一维数组的第一个值赋值为1,剩余赋值为0,然后从后向前按照杨辉三角的规律推断前面的值。
这里需要注意边界、特殊值的处理,防止数组越界。
具体的实现过程如下代码所示:
void YangHui1_1(const int n) //一维数组实现杨辉三角(只用一个一维数组)
{//int* arr = (int*)malloc(n * sizeof(int)); //动态申请一个一维数组arr//利用calloc动态申请n*sizeof(int)大小空间之后,会将里面的值全部初始化为0int* arr = (int*)calloc(n, sizeof(int)); //注意此处为什么要用calloc,而不用malloc/*【注】此处用calloc,注意calloc和malloc的区别calloc:在内存的动态存储区中分配n个长度为sizeof(int)的连续空间,不同点:calloc在动态分配完内存后,自动初始化该内存空间为【零】,而malloc不初始化,里边数据是随机的垃圾数据*/assert(arr != NULL); //断言arr[0] = 1; //将数组的第一个值赋值为1for (int i = 0; i < n; i++) //此层循环是处理第i行的数据,也就是控制层数{//此方法是一维数组的第一个值赋值为1,剩余赋值为0,然后从后向前推for (int j = i; j >= 1; j--){//若从后向前处理,当i=0时,不需要处理(循环进不去),当i=1时,也就是第2行,只需处理一个值/*1 0 0 0 0 0 0 0 01 1 0 0 0 0 0 0 01 2 1 0 0 0 0 0 01 3 3 1 0 0 0 0 0*///第一列不需要处理,从后向前,也即j>=1是退出条件arr[j] = arr[j] + arr[j - 1]; //当前值 == 当前值(初始均为0)+ 上一个位置的值}for (int k = 0; k <= i; k++) //小于等于i是因为第i行只需要打印i个值{printf("%-5d", arr[k]);}printf("\n");}free(arr); //利用malloc后,要释放指针arr
}
这里打印10行杨辉三角,运行结果如下:

三、不用数组实现杨辉三角
不用数组实现杨辉三角,这里利用for循环实现:
第一个数是1;
第二个数是:1*(n - 1)/1;
第三个数是:1*(n - 1)/1 * (n - 2 )/2;
第四个数是:1*(n - 1)/1 * (n - 2 )/2 * (n - 3)/3
根据规律得到计算公式:tmp = tmp * (i - (j - 1))/(j - 1); //用到上一个值*(i - (j - 1))/(j - 1)
具体的实现过程如下代码所示:
int YangHui(const int n) //不用数组实现杨辉三角,利用for循环直接实现杨辉三角
{//第n行:第一个数是1;第二个数是:1*(n - 1)/1;第三个数是:1*(n - 1)/1 * (n - 2 )/2;// 第四个数是:1*(n - 1)/1 * (n - 2 )/2 * (n - 3)/3//tmp = tmp * (i - (j - 1))/(j - 1); //用到上一个值*(i - (j - 1))/(j - 1)if (n < 0){return -1;}int tmp = 0; //先申请一个变量tmpfor (int i = 1; i <= n; i++) //此处是从第一行开始,处理每一层的数据{for (int j = 1; j <= i; j++) //注意此处是从下标1开始的,也就是第一列的列下标均为1{if (j == 1) //每一行的第一个值特殊处理,其它的值均用公式,从后向前推导{tmp = 1; //第一列的值均为1,第一列作为特殊列处理}else{tmp = tmp * (i - (j - 1)) / (j - 1); //公式}printf("%-5d", tmp);}printf("\n");}
}
这里打印10行杨辉三角,运行结果如下: