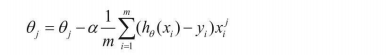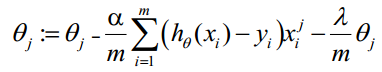文章目录
- 引言
- 逻辑回归算法原理
- 逻辑回归损失函数
- python实现逻辑回归
- 决策边界
- python实现多项式逻辑回归
- sklearn中的逻辑回归
- 逻辑回归中的正则化
- sklearn实现逻辑回归
引言
逻辑回归(Logistic Regression)是一种分类学习算法,其本质是将样本的特征和样本发生的概率联系起来,由于发生的概率是一个数值,因此称为回归算法。主要解决2分类问题,例如:一个垃圾邮件过滤系统,x是邮件的特征,预测的y值就是邮件的类别(是垃圾邮件还是正常邮件)。
逻辑回归算法原理
逻辑回归算法步骤如下
- 计算样本发生的概率值,即 p ^ = f ( x ) \hat p=f(x) p^=f(x)
- 根据样本发生的概率分类 y ^ = { 1 , p ^ ≥ 0.5 0 , p ^ ≤ 0.5 \hat y= \begin{cases} 1 \ , \ \hat p\geq 0.5\\ 0 \ , \ \hat p\leq 0.5\\ \end{cases} y^={1 , p^≥0.50 , p^≤0.5
逻辑回归算法既可以看作回归算法,也可以看作分类算法,只执行第一步时就是回归算法,但是逻辑回归算法通常作为回归算法用,主要解决2分类问题。在线性回归算法中,样本预测值
y ^ = f ( x ) = θ T ⋅ x b \hat y=f(x)= \theta ^{T} \cdot x_b y^=f(x)=θT⋅xb
其值域为( − ∞ , + ∞ -\infty , + \infty −∞,+∞),而概率的值域为[0,1],因此需要对 f ( x ) f(x) f(x)函数进行处理,使之值域处于[0,1]
即 p ^ = σ ( θ T ⋅ x b ) \hat p=\sigma( \theta ^{T} \cdot x_b ) p^=σ(θT⋅xb),一般
σ ( t ) = 1 1 + e − t \sigma(t) = \frac{1}{1+e^{-t}} σ(t)=1+e−t1
σ ( t ) \sigma(t) σ(t)值域为(0,1),当t>0时,p>0.5;当t<0时,p<0.5

逻辑回归损失函数
模型预测值 y ^ \hat y y^ 如下
y ^ = { 1 , p ^ ≥ 0.5 0 , p ^ ≤ 0.5 \hat y= \begin{cases} 1 \ , \ \hat p\geq 0.5\\ 0 \ , \ \hat p\leq 0.5\\ \end{cases} y^={1 , p^≥0.50 , p^≤0.5
由此可以看出当实际值y=1时,p越小,损失越大;当y=0时,p越大,损失越大,即
c o s t = { y = 1 时 , p 越 小 , 损 失 越 大 y = 0 时 , p 越 大 , 损 失 越 大 cost= \begin{cases} y=1时,p越小,损失越大 \\ y=0时,p越大,损失越大\end{cases} cost={y=1时,p越小,损失越大y=0时,p越大,损失越大
下面函数刚好满足条件
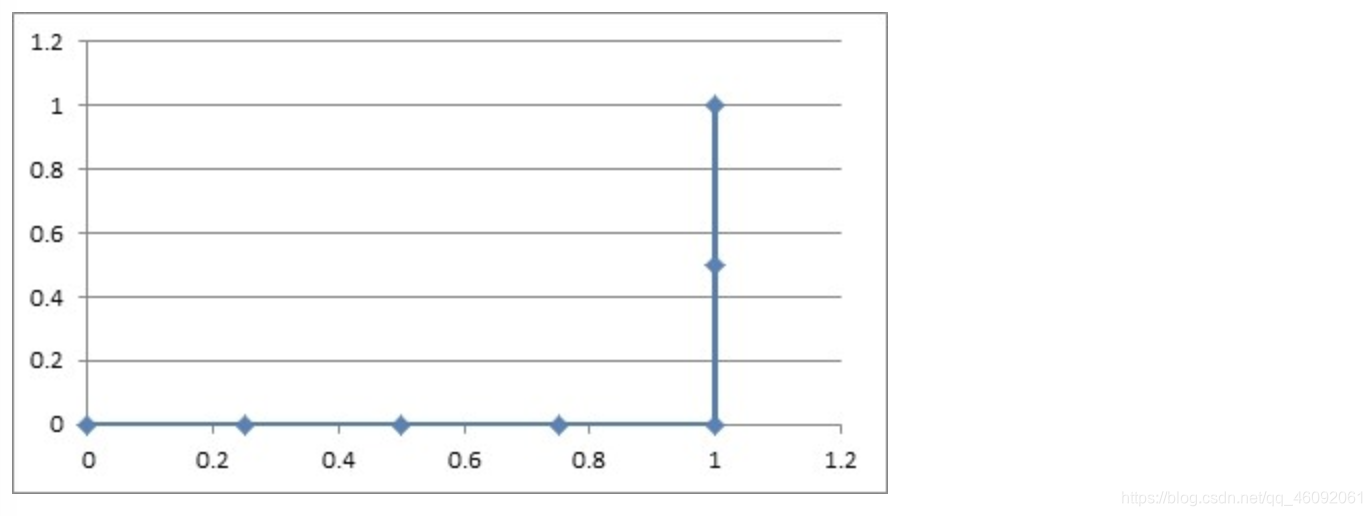
c o s t = { − l o g ( p ^ ) , i f y = 1 − l o g ( 1 − p ^ ) , i f y = 0 cost= \begin{cases} -log(\hat p) \ ,\ \ \ \ \ \ \ if \ \ y=1\\ -log(1-\hat p) \ ,if \ \ y=0\\ \end{cases} cost={−log(p^) , if y=1−log(1−p^) ,if y=0
画出cost函数图像可以看出,当样本实际值为1时,预测概率值x为0, − log ( x ) -\log(x) −log(x)趋于正无穷,即损失趋于正无穷,当x=1即符合实际值,损失为0;当样本实际值为0时,预测值概率值x为1, − log ( 1 − x ) -\log(1-x) −log(1−x)趋于正无穷,即损失趋于正无穷,当x=0即符合实际值,损失为0。

损失函数可以合为1个,即

最终得到损失函数
J ( θ ) = − 1 m ∑ i = 1 m y ( i ) + log ( p ^ ( i ) ) + ( 1 − y ( i ) ) log ( 1 − p ^ ( i ) ) J(\theta)=-\frac {1}{m} \sum_{i=1}^{m}{y^{(i)}+\log(\hat p^{(i)})+(1-y^{(i)})\log(1-\hat p^{(i)})} J(θ)=−m1i=1∑my(i)+log(p^(i))+(1−y(i))log(1−p^(i))
p ^ ( i ) = σ ( X b ( i ) θ ) = 1 1 + e − X b ( i ) θ \hat p^{(i)}=\sigma(X_b^{(i)}\theta)=\frac{1}{1+e^{-X_b^{(i)}\theta}} p^(i)=σ(Xb(i)θ)=1+e−Xb(i)θ1
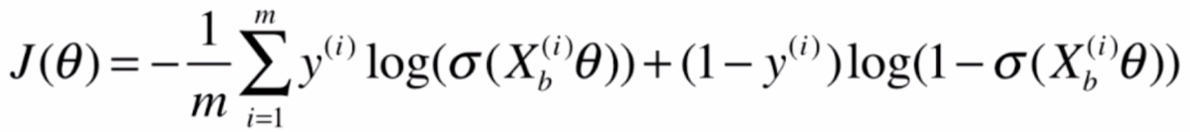
最后可以通过梯度下降法,求出使损失函数最小的 θ \theta θ,求得的损失函数梯度如下

python实现逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_splitclass LogisticRegression:def __init__(self):self.coef_ = Noneself.intercept_ = Noneself._theta = Nonedef _sigmoid(self, t):return 1 / (1 + np.exp(-t))def fit(self, x_train, y_trian, n):def J(theta, x_b, y):y_hat = self._sigmoid(x_b.dot(theta))return -np.sum(y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)) / len(y)def dJ(theta, x_b, y):return x_b.T.dot(self._sigmoid(x_b.dot(theta)) - y) / len(y)def gradient_descent(x_b, y, initial_theta, alpha=0.01, n_iters=1e4, epsilon=1e-8):theta = initial_thetaiter = 0while iter < n_iters:gradient = dJ(theta, x_b, y)last_theta = thetatheta = theta - alpha * gradientif abs(J(last_theta, x_b, y) - J(theta, x_b, y)) < epsilon:breakiter += 1return last_thetax_b = np.hstack([np.ones((len(x_train), 1)), x_train])initail_theta = np.zeros(x_b.shape[1])self._theta = gradient_descent(x_b, y_trian, initail_theta, n_iters=n)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]def predict_prob(self, x_test):x_b = np.hstack([np.ones((len(x_test), 1)), x_test])return self._sigmoid(x_b.dot(self._theta))def predict(self, x_test):prob = self.predict_prob(x_test)return np.array(prob >= 0.5,dtype='int')def score(self, x_test, y_test):return np.sum(y_test == self.predict(x_test)) / len(y_test)# 鸢尾花数据集测试手写逻辑回归算法
iris = load_iris()
x = iris.data
y = iris.target# 由于逻辑回归只能处理2分类问题,截取分类为0,1,保留x2个特征方便可视化
X = x[y < 2, :2]
Y = y[y < 2]plt.scatter(X[Y == 0, 0], X[Y == 0, 1])
plt.scatter(X[Y == 1, 0], X[Y == 1, 1], color='r')
plt.show()x_train, x_test, y_train, y_test = train_test_split(X, Y)logistic = LogisticRegression()
logistic.fit(x_train, y_train, n=1e6)
y_predict = logistic.predict(x_test)
score = logistic.score(x_test, y_test)
print(score)
print(y_predict)
print(y_test)输出
1.0
[0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 0 0 1 1 0 1 0 1 1 1]
[0 1 1 1 0 0 0 0 0 1 1 0 1 1 1 0 0 1 1 0 1 0 1 1 1]
决策边界
决策边界就是能够把样本正确分类的一条边界
p ^ = σ ( X b ⋅ θ ) = 1 1 + e − X b ⋅ θ \hat p=\sigma(X_b \cdot \theta)=\frac{1}{1+e^{-X_b \cdot \theta}} p^=σ(Xb⋅θ)=1+e−Xb⋅θ1
y ^ = { 1 , p ^ ≥ 0.5 0 , p ^ ≤ 0.5 \hat y= \begin{cases} 1 \ , \ \hat p\geq 0.5\\ 0 \ , \ \hat p\leq 0.5\\ \end{cases} y^={1 , p^≥0.50 , p^≤0.5
当 p ^ = 0.5 \hat p=0.5 p^=0.5时,=> X b ⋅ θ = 0 X_b \cdot \theta=0 Xb⋅θ=0, 即为决策边界
(1) 当样本空间只有2个特征情况,即
θ 0 + x 1 θ 1 + x 2 θ 2 = 0 \theta_0+x_1 \theta_1+x_2 \theta_2=0 θ0+x1θ1+x2θ2=0
x 2 = − θ 0 − x 1 θ 1 θ 2 x_2=\frac{-\theta_0-x_1 \theta_1}{\theta_2} x2=θ2−θ0−x1θ1
绘制 x 1 , x 2 x_1,x_2 x1,x2关系直线图
x_1 = np.linspace(4, 7, 100)
x_2 = (-logistic.intercept_ - x_1 * logistic.coef_[0]) / logistic.coef_[1]
plt.plot(x_1, x_2)
plt.show()

(2)不规则决策边界绘制
把整个区域看成无数个点,用得出的模型去预测这些点,不同分类用不同颜色区分
def plot_decision_boundary(model, axis):# x/y轴矩阵,如x:0-2,y:0-1,得到x=[[0, 1, 2],[0, 1, 2]],y=[[0, 0, 0],[1, 1, 1]]x, y = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1))# 矩阵拼接,如x:0-2,y:0-1,得到[[0. 0.], [1. 0.], [2. 0.], [0. 1.], [1. 1.], [2. 1.]]x_new = np.c_[x.reshape(-1), y.reshape(-1)]y_predict = model.predict(x_new)zz = y_predict.reshape(x.shape)custom_cmap = ListedColormap(['#EF9A9A', '#EFF59D', '#90CAF9'])plt.contourf(x, y, zz, linewidth=5, cmap=custom_cmap)python实现多项式逻辑回归
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScalerclass LogisticRegression:def __init__(self):self.coef_ = Noneself.intercept_ = Noneself._theta = Nonedef _sigmoid(self, t):return 1 / (1 + np.exp(-t))def fit(self, x_train, y_trian, n=1e4):def J(theta, x_b, y):y_hat = self._sigmoid(x_b.dot(theta))return -np.sum(y * np.log(y_hat) + (1. - y) * np.log(1. - y_hat)) / len(y)def dJ(theta, x_b, y):return x_b.T.dot(self._sigmoid(x_b.dot(theta)) - y) / len(x_b)def gradient_descent(x_b, y, initial_theta, alpha=0.01, n_iters=1e4, epsilon=1e-8):theta = initial_thetaiter = 0while iter < n_iters:gradient = dJ(theta, x_b, y)last_theta = thetatheta = theta - alpha * gradientif abs(J(last_theta, x_b, y) - J(theta, x_b, y)) < epsilon:breakiter += 1return last_thetax_b = np.hstack([np.ones((len(x_train), 1)), x_train])initail_theta = np.zeros(x_b.shape[1])self._theta = gradient_descent(x_b, y_trian, initail_theta, n_iters=n)self.intercept_ = self._theta[0]self.coef_ = self._theta[1:]def predict_prob(self, x_test):x_b = np.hstack([np.ones((len(x_test), 1)), x_test])return self._sigmoid(x_b.dot(self._theta))def predict(self, x_test):prob = self.predict_prob(x_test)return np.array(prob >= 0.5, dtype='int')def score(self, x_test, y_test):return np.sum(y_test == self.predict(x_test)) / len(y_test)def plot_decision_boundary(model, axis):# x/y轴矩阵,如x:0-2,y:0-1,得到x=[[0, 1, 2],[0, 1, 2]],y=[[0, 0, 0],[1, 1, 1]]x, y = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1))# 矩阵拼接,如x:0-2,y:0-1,得到[[0. 0.], [1. 0.], [2. 0.], [0. 1.], [1. 1.], [2. 1.]]x_new = np.c_[x.reshape(-1), y.reshape(-1)]y_predict = model.predict(x_new)zz = y_predict.reshape(x.shape)custom_cmap = ListedColormap(['#EF9A9A', '#EFF59D', '#90CAF9'])plt.contourf(x, y, zz, linewidth=5, cmap=custom_cmap)# 测试数据集
x = np.random.normal(0, 1, size=(200, 2))
y = np.array(x[:, 0] ** 2 + x[:, 1] ** 2 < 1.5, dtype='int')
x_train, x_test, y_train, y_test = train_test_split(x, y)pip = Pipeline([('poly', PolynomialFeatures(degree=10)),('std', StandardScaler()),('logistic', LogisticRegression())
])
pip.fit(x_train, y_train)
score = pip.score(x_test, y_test)
print(score)plt.scatter(x[y == 0, 0], x[y == 0, 1])
plt.scatter(x[y == 1, 0], x[y == 1, 1])
plt.show()
sklearn中的逻辑回归
逻辑回归中的正则化
在多项式回归当中添加正则化模型后的损失函数为 J ( θ ) + α L J(\theta)+\alpha L J(θ)+αL,而在逻辑回归当中,模型正则化通常为 C ⋅ J ( θ ) + L 1 C\cdot J(\theta)+L_1 C⋅J(θ)+L1或者 C ⋅ J ( θ ) + L 2 C\cdot J(\theta)+L_2 C⋅J(θ)+L2,L1、L2对应2种正则项,如果C越大,优化损失函数时越应该集中火力,将损失函数减小到最小;C非常小时,此时L1和L2的正则项就显得更加重要。
sklearn实现逻辑回归
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
import numpy as np
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormapdef plot_decision_boundary(model, axis):# x/y轴矩阵,如x:0-2,y:0-1,得到x=[[0, 1, 2],[0, 1, 2]],y=[[0, 0, 0],[1, 1, 1]]x, y = np.meshgrid(np.linspace(axis[0], axis[1], int((axis[1] - axis[0]) * 100)).reshape(-1, 1),np.linspace(axis[2], axis[3], int((axis[3] - axis[2]) * 100)).reshape(-1, 1))# 矩阵拼接,如x:0-2,y:0-1,得到[[0. 0.], [1. 0.], [2. 0.], [0. 1.], [1. 1.], [2. 1.]]x_new = np.c_[x.reshape(-1), y.reshape(-1)]y_predict = model.predict(x_new)zz = y_predict.reshape(x.shape)custom_cmap = ListedColormap(['#EF9A9A', '#EFF59D', '#90CAF9'])plt.contourf(x, y, zz, linewidth=5, cmap=custom_cmap)# 测试数据集
x = np.random.normal(0, 1, size=(200, 2))
y = np.array(x[:, 0] ** 2 + x[:, 1] ** 2 < 1.5, dtype='int')
x_train, x_test, y_train, y_test = train_test_split(x, y)pip = Pipeline([('poly', PolynomialFeatures(degree=10)),('std', StandardScaler()),('logistic', LogisticRegression(C=1., penalty='l2'))
])pip.fit(x_train, y_train)
score = pip.score(x_test, y_test)
print(score)plot_decision_boundary(pip, axis=[-4, 4, -4, 4])
plt.scatter(x[y == 0, 0], x[y == 0, 1])
plt.scatter(x[y == 1, 0], x[y == 1, 1])
plt.show()