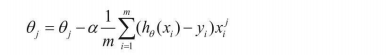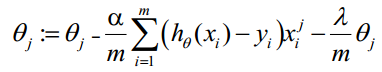---

一、逻辑回归简介

1.1 什么是逻辑回归

逻辑回归（Logistic Regression）是一种用于解决二分类（0 or 1）问题的机器学习方法，用于估计某种事物的可能性。比如某用户购买某商品的可能性，某病人患有某种疾病的可能性，以及某广告被用户点击的可能性等。

逻辑回归不是一个回归算法！而是一个分类算法！

逻辑回归的决策边界可以是非线性的

逻辑回归是最简单的分类算法。通常来说在进行分类任务时，我们都会用逻辑回归做一个BaseLine，然后再尝试其他算法不断改进。

逻辑回归不是只能做二分类，它也可以做多分类问题！

1.2 Sigmoid函数

Sigmoid函数是逻辑回归实现非线性决策边界的基础

Sigmoid函数的公式:

$$g(z)=\frac{1}{1+e^{-z}}$$

特点：自变量取值为任意实数，值域 $[0,1]$

解释: 将任意的输入映射到了[0,1]区间 $-\infty$我们在线性回归中可以得到一个预测值，再将该值映射到Sigmoid 函数 中这样就完成了由值到概率的转换，也就是分类任务

绘制Sigmoid函数：

x = np.arange(-10, 10, 0.01)
y = 1 / (1 + np.exp(-x))
plt.plot(x, y)
plt.plot([0, 0], [max(y), min(y)], 'r--', alpha=0.4)
plt.plot([max(x), min(x)], [0, 0], 'r--', alpha=0.4)
plt.xlabel("$x$")
plt.ylabel("$y$")
plt.show()

1.3 预测函数

预则函数 :

$$h_{\theta }(x)=g\left({\theta }^{T}x\right)=\frac{1}{1+e^{-{\theta }^{T}x}}$$

其中

$${\theta }_0+{\theta }_1{x}_1+,\dots ,+{\theta }_n{x}_n=\sum _{i=1}^n{\theta }_i{x}_i={\theta }^{T}x$$

分类任务：

$$\begin{array}{rl}& P(y=1\mid x;\theta )=h_{\theta }(x)\\ & P(y=0\mid x;\theta )=1-h_{\theta }(x)\end{array}$$

整合 :

$$P(y\mid x;\theta )={\left(h_{\theta }(x)\right)}^y{\left(1-h_{\theta }(x)\right)}^{1-y}$$

解释 : 对于二分类任务 $(0，1)$ ，整合后y取0只保留 ${\left(1-h_{\theta }(x)\right)}^{1-y}$ ； $\mathrm{y}$ 取1只保留 ${\left(h_{\theta }(x)\right)}^y$

似然函数 :

$$L(\theta )=\prod _{i=1}^{m}P\left(y_i\mid x_i;\theta \right)=\prod _{i=1}^m{\left(h_{\theta }\left(x_i\right)\right)}^{y_i}{\left(1-h_{\theta }\left(x_i\right)\right)}^{1-y_i}$$

对数似然 :

$$l(\theta )=\log L(\theta )=\sum _{i=1}^m\left(y_i\log h_{\theta }\left(x_i\right)+\left(1-y_i\right)\log \left(1-h_{\theta }\left(x_i\right)\right)\right)$$

此时应用梯度上升求最大值，引入 $J(\theta )=-\frac{1}{m}l(\theta )$ 转换为梯度下降任务

求导过程 :

$$\begin{array}{rl}& l(\theta )=\log L(\theta )=\sum _{i=1}^m\left(y_i\log h_{\theta }\left(x_i\right)+\left(1-y_i\right)\log \left(1-h_{\theta }\left(x_i\right)\right)\right)\\ & \frac{\delta }{{\delta }_{\theta }}J(\theta )=-\frac{1}{m}\sum _{i=1}^m\left(y_i\frac{1}{h_{\theta }\left(x_i\right)}\frac{\delta }{{\delta }_{\theta }}{h}_{\theta }\left(x_i\right)-\left(1-{\mathrm{y}}_{\mathrm{i}}\right)\frac{1}{1-h_{\theta }\left(x_i\right)}\frac{\delta }{{\delta }_{\theta }}{h}_{\theta }\left(x_i\right)\right)\\ =& -\frac{1}{m}\sum _{i=1}^m\left(y_i\frac{1}{g\left({\theta }^{\mathrm{T}}{x}_i\right)}-\left(1-{\mathrm{y}}_{\mathrm{i}}\right)\frac{1}{1-g\left({\theta }^{\mathrm{T}}{x}_i\right)}\right)\frac{\delta }{{\delta }_j}g\left({\theta }^{\mathrm{T}}{x}_i\right)\\ =& -\frac{1}{m}\sum _{i=1}^m\left(y_i\frac{1}{g\left({\theta }^{\mathrm{T}}{x}_i\right)}-\left(1-{\mathrm{y}}_{\mathrm{i}}\right)\frac{1}{1-g\left({\theta }^{\mathrm{T}}{x}_i\right)}\right)g\left({\theta }^{\mathrm{T}}{x}_i\right)\left(1-g\left({\theta }^{\mathrm{T}}{x}_i\right)\right)\frac{\delta }{{\delta }_{\theta }}{\theta }^{\mathrm{T}}{x}_i\\ & =-\frac{1}{m}\sum _{i=1}^m\left(y_i\left(1-g\left({\theta }^{\mathrm{T}}{x}_i\right)\right)-\left(1-{\mathrm{y}}_{\mathrm{i}}\right)g\left({\theta }^{\mathrm{T}}{x}_i\right)\right)x_i^j\\ =& -\frac{1}{m}\sum _{i=1}^m\left(y_i-g\left({\theta }^{\mathrm{T}}{x}_i\right)\right)x_i^j\end{array}$$

参数更新 :

$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }\left(x_i\right)-y_i\right)x_i^j$$

多分类的softmax:

$$h_{\theta }\left(x^{(i)}\right)=\left[\begin{array}{c}p\left(y^{(i)}=1\mid x^{(i)};\theta \right)\\ p\left(y^{(i)}=2\mid x^{(i)};\theta \right)\\ ⋮\\ p\left(y^{(i)}=k\mid x^{(i)};\theta \right)\end{array}\right]=\frac{1}{{\sum }_{j=1}^k{e}^{{\theta }_j^T{x}^{(i)}}}\left[\begin{array}{c}{e}^{oT}{x}^{(i)}\\ e^{{\sigma }_2^T{x}^{(i)}}\\ ⋮\\ ⋮\\ e^{T_k^{(i)}{x}^{(i)}}\end{array}\right]$$

总结 : 逻辑回归真的真的很好很好用 !

二、逻辑回归实战 - Java代码实现

TrainDataSet ：训练集对象

public class TrainDataSet {/*** 特征集合**/public List<double[]> features = new ArrayList<>();/*** 标签集合**/public List<Double> labels = new ArrayList<>();/*** 特征向量维度**/public int featureDim;public int size() {return labels.size();}public double[] getFeature(int index) {return features.get(index);}public double getLabel(int index) {return labels.get(index);}public void addData(double[] feature, double label) {if (features.isEmpty()) {featureDim = feature.length;} else {if (featureDim != feature.length) {throwDimensionMismatchException(feature.length);}}features.add(feature);labels.add(label);}public void throwDimensionMismatchException(int errorLen) {throw new RuntimeException("DimensionMismatchError: 你应该传入维度为 " + featureDim + " 的特征向量 , 但你传入了维度为 " + errorLen + " 的特征向量");}}

LogisticRegression: 逻辑回归算法对象

public class LogisticRegression {/*** 训练数据集**/TrainDataSet trainDataSet;/*** 学习率**/double lr;/*** 最大迭代次数**/int epochs;/*** 权重参数矩阵**/double[] weights;/*** 最佳权重参数矩阵**/double[] bestWeights;/*** 最佳准确率**/double bestAcc;/*** @param trainDataSet: 训练数据集* @param lr:           学习率* @param epochs:       最大迭代次数*/public LogisticRegression(TrainDataSet trainDataSet, double lr, int epochs) {this.trainDataSet = trainDataSet;this.lr = lr;this.epochs = epochs;}// 初始化模型public void initModel() {weights = new double[trainDataSet.featureDim];bestWeights = new double[trainDataSet.featureDim];bestAcc = 0d;}// 训练函数public void fit() {initModel();for (int epoch = 1; epoch <= epochs; epoch++) {// 对整个训练集进行预测double[] predicts = new double[trainDataSet.size()];for (int i = 0; i < predicts.length; i++) {predicts[i] = sigmoid(dotProduct(weights, trainDataSet.getFeature(i)));}// 计算 MSE-Lossdouble loss = 0d;for (int i = 0; i < predicts.length; i++) {loss += Math.pow(predicts[i] - trainDataSet.getLabel(i), 2);}loss /= trainDataSet.size();double acc = calcAcc(predicts);if (epoch % 1000 == 0 || epoch == 1) {System.out.println("epoch: " + epoch + " , loss: " + loss + " , acc: " + acc);}if (acc > bestAcc) {bestAcc = acc;bestWeights = weights.clone();}// 梯度下降法更新参数double[] diffs = new double[trainDataSet.size()];for (int i = 0; i < trainDataSet.size(); i++) {diffs[i] = trainDataSet.getLabel(i) - predicts[i];}for (int i = 0; i < weights.length; i++) {double step = 0d;for (int j = 0; j < trainDataSet.size(); j++) {step += trainDataSet.getFeature(j)[i] * diffs[j];}step = step / trainDataSet.size();weights[i] += (lr * step);}}}// 计算正确率private double calcAcc(double[] predicts) {int acc = 0;for (int i = 0; i < trainDataSet.size(); i++) {if ((int) Math.round(predicts[i]) == trainDataSet.getLabel(i)) {acc++;}}return (double) acc / trainDataSet.size();}// 传入特征，返回预测值（用最佳的权重矩阵进行预测）public int predict(double[] feature) {if (feature.length != trainDataSet.featureDim) {trainDataSet.throwDimensionMismatchException(feature.length);}return (int) Math.round(sigmoid(dotProduct(bestWeights, feature)));}// 向量点积private double dotProduct(double[] vector1, double[] vector2) {double res = 0d;for (int i = 0; i < vector1.length; i++) {res += (vector1[i] * vector2[i]);}return res;}// sigmoid 函数public double sigmoid(double x) {return 1.0 / (1.0 + Math.exp(-x));}}

Run: 测试类

public class Run {public static void main(String[] args) {// 随机数种子long seed = 929L;// 训练集大小int dataSize = 100;// 特征向量维度数int featureDim = 60;// 随机构造数据集TrainDataSet trainDataSet = createRandomTrainDataSet(seed, dataSize, featureDim);// 开始逻辑回归算法long startTime = System.currentTimeMillis();LogisticRegression logisticRegression = new LogisticRegression(trainDataSet, 2e-03, 50000);logisticRegression.fit();System.out.println("用时: " + (System.currentTimeMillis() - startTime) / 1000d + " s");}// 随机生成测试数据public static TrainDataSet createRandomTrainDataSet(long seed, int dataSize, int featureDim) {TrainDataSet trainDataSet = new TrainDataSet();Random random = new Random(seed);for (int i = 0; i < dataSize; i++) {double[] feature = new double[featureDim];double sum = 0d;for (int j = 0; j < feature.length; j++) {feature[j] = random.nextDouble();sum += feature[j];}double label = sum >= 0.5 * featureDim ? 1 : 0;trainDataSet.addData(feature, label);}return trainDataSet;}}

输出：

epoch: 1 , loss: 0.25 , acc: 0.57
epoch: 1000 , loss: 0.23009206054491824 , acc: 0.57
epoch: 2000 , loss: 0.22055342908355904 , acc: 0.57
epoch: 3000 , loss: 0.2119690514733919 , acc: 0.62
epoch: 4000 , loss: 0.20424003587074643 , acc: 0.68
epoch: 5000 , loss: 0.19727002863958823 , acc: 0.71
epoch: 6000 , loss: 0.19096949150899337 , acc: 0.72
epoch: 7000 , loss: 0.18525745498286608 , acc: 0.77
epoch: 8000 , loss: 0.18006202781346625 , acc: 0.77
epoch: 9000 , loss: 0.1753201537243613 , acc: 0.8
epoch: 10000 , loss: 0.1709769595639883 , acc: 0.8
epoch: 11000 , loss: 0.16698491959902464 , acc: 0.79
epoch: 12000 , loss: 0.16330297319030188 , acc: 0.82
epoch: 13000 , loss: 0.15989567356751072 , acc: 0.84
epoch: 14000 , loss: 0.1567324071471881 , acc: 0.84
epoch: 15000 , loss: 0.15378669947061832 , acc: 0.84
epoch: 16000 , loss: 0.15103561034798546 , acc: 0.84
epoch: 17000 , loss: 0.14845921356649672 , acc: 0.84
epoch: 18000 , loss: 0.1460401531041619 , acc: 0.85
epoch: 19000 , loss: 0.143763266598652 , acc: 0.85
epoch: 20000 , loss: 0.141615266856612 , acc: 0.85
epoch: 21000 , loss: 0.13958447284858422 , acc: 0.85
epoch: 22000 , loss: 0.1376605825635673 , acc: 0.85
epoch: 23000 , loss: 0.1358344810954265 , acc: 0.85
epoch: 24000 , loss: 0.13409807829499976 , acc: 0.85
epoch: 25000 , loss: 0.13244417119628302 , acc: 0.85
epoch: 26000 , loss: 0.13086632719356164 , acc: 0.85
epoch: 27000 , loss: 0.12935878460708283 , acc: 0.85
epoch: 28000 , loss: 0.12791636783482388 , acc: 0.85
epoch: 29000 , loss: 0.12653441475794497 , acc: 0.85
epoch: 30000 , loss: 0.12520871445955495 , acc: 0.85
epoch: 31000 , loss: 0.12393545364204453 , acc: 0.85
epoch: 32000 , loss: 0.12271117039803882 , acc: 0.85
epoch: 33000 , loss: 0.12153271421325021 , acc: 0.85
epoch: 34000 , loss: 0.12039721126413588 , acc: 0.85
epoch: 35000 , loss: 0.11930203422599839 , acc: 0.85
epoch: 36000 , loss: 0.11824477593360722 , acc: 0.85
epoch: 37000 , loss: 0.1172232263412268 , acc: 0.85
epoch: 38000 , loss: 0.11623535231592816 , acc: 0.86
epoch: 39000 , loss: 0.11527927987040722 , acc: 0.86
epoch: 40000 , loss: 0.11435327850180353 , acc: 0.86
epoch: 41000 , loss: 0.11345574735333493 , acc: 0.86
epoch: 42000 , loss: 0.11258520295767636 , acc: 0.86
epoch: 43000 , loss: 0.11174026835632704 , acc: 0.86
epoch: 44000 , loss: 0.11091966341890613 , acc: 0.86
epoch: 45000 , loss: 0.11012219621134119 , acc: 0.86
epoch: 46000 , loss: 0.10934675528306022 , acc: 0.86
epoch: 47000 , loss: 0.10859230276120614 , acc: 0.86
epoch: 48000 , loss: 0.10785786815509599 , acc: 0.86
epoch: 49000 , loss: 0.10714254278709882 , acc: 0.86
epoch: 50000 , loss: 0.10644547477714164 , acc: 0.86