1.点到平面的距离

首先说一下采用向量法计算点到平面的距离：

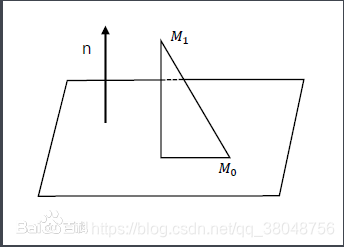
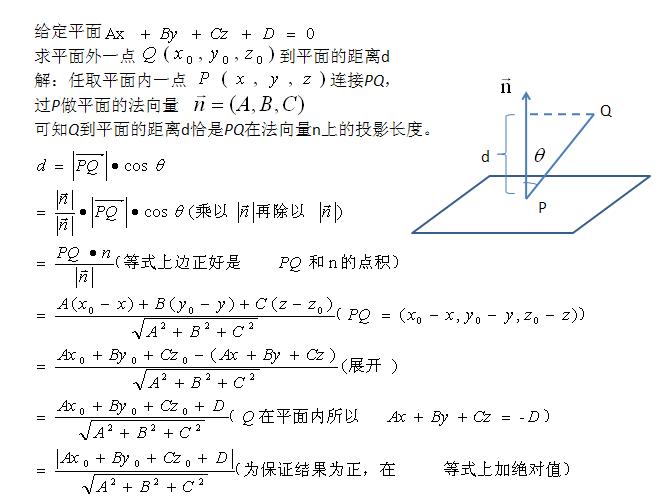
设图中平面的方程为Ax+By+Cz+D=0,点M₀的坐标为（x0,y0,z0）,点M₁的坐标为（x1,y1,z1）,求M₁到平面的距离。

解：

其中a为向量M₀M₁与平面法向量之间的夹角，对于平面Ax+By+Cz+D=0，该平面的一个法向量n为（A，B，C）,由于

因此

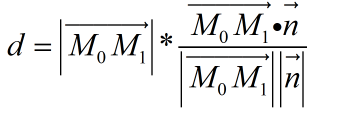
进一步化简该式：

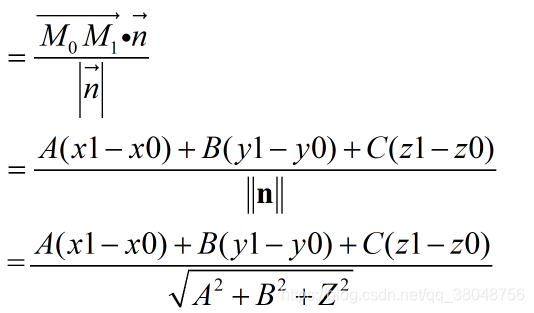
由于点M₀在平面内，故有

故结果可进一步转化为

因为距离为正数，因此此处加了个绝对值。
综上可以看出，点到平面的距离的计算，实际上是将该点带入到该平面方程，然后再除以该平面的法向量的二范数。

注：
1.向量的模为向量的长度
2.向量的点积为一个数
3.向量的二范数为向量所有元素的平方和再开根号。

2.点到超平面的距离

由点到平面的距离，可以类比下点到超平面的距离，即将该点带入到该超平面，然后再除以该平面法向量的二范数。实际应用中。通常将该点带入到该超平面，不除以该平面法向量的二范数，利用该方式来刻画点到超平面的距离远近。