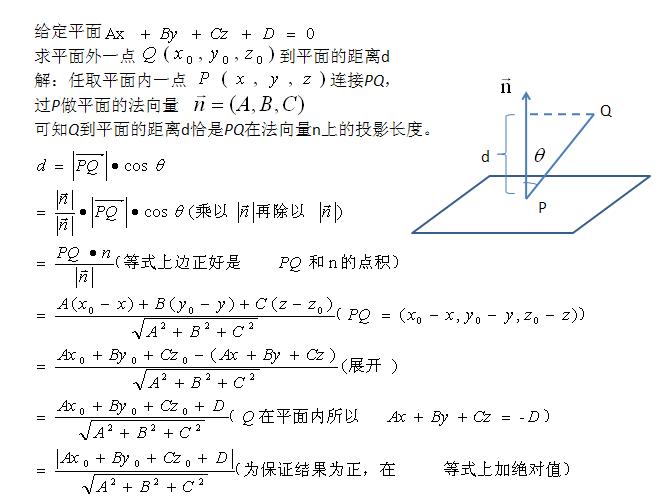
1.空间中平面方程的一般形式为：

Ax+By+Cz+D=0 (参数,A,B,C,D是描述平面空间特征的常数)

已知空间中3个点的坐标(x1,y1,z1),(x2,y2,z2),(x3,y3,z3)，求解平面方程。

解法1.根据已知的3个点，建立3个联合方程组，进行消元；
2.根据克莱姆法则，
代码：

    //求点到平面的距离public double PointToFaceDistance(XYZ point1,XYZ point2,XYZ point3,XYZ p0){矩阵的定义和初始化//var matrix1 = new DenseMatrix(3);    //3维方阵//var matrix2 = new DenseMatrix(3,2);   //3×2矩阵double S = 0;double[,] a = { { 1, 1, 1 }, { point1.Y, point2.Y, point3.Y }, { point1.Z, point2.Z, point3.Z } };double[,] b = { { point1.X, point2.X, point3.X }, { 1, 1, 1 }, { point1.Z, point2.Z, point3.Z } };double[,] c = { { point1.X, point2.X, point3.X }, { point1.Y, point2.Y, point3.Y }, { 1, 1, 1 } };double[,] d = { { point1.X, point2.X, point3.X }, { point1.Y, point2.Y, point3.Y }, { point1.Z, point2.Z, point3.Z } };DenseMatrix matrix1 = DenseMatrix.OfArray(a);DenseMatrix matrix2 = DenseMatrix.OfArray(b);DenseMatrix matrix3 = DenseMatrix.OfArray(c);DenseMatrix matrix4 = DenseMatrix.OfArray(d);          double A = matrix1.Determinant();double B = matrix2.Determinant();double C = matrix3.Determinant();double D = matrix4.Determinant();S = Math.Abs(A * p0.X + B * p0.Y + C * p0.Z + D) / Math.Sqrt(A*A+B*B+C*C);return S;}