平面的点法式方程

法向量：垂直于一个平面的非零向量叫做一个平面的法向量。
假设空间内有一点$M_0(x_0, y_0, z_0)$和一个向量$\overrightarrow n = (A, B, C)$，则经过点$M_0$且垂直于向量$\overrightarrow n$的平面有且只有一个，记为$\Pi$，它的法向量即是$\overrightarrow n$。

设在平面$\Pi$上有除了$M_0$外的一点$M(x, y, z)$，则必有$\overrightarrow {M_0M} \bot \overrightarrow n$，即它们的数量积为零

$$\overrightarrow n ·\overrightarrow {M_0M} = 0$$ $$A(x - x_0) + B(y - y_0) + C(z - z_0) = 0$$

这就是平面$\Pi$的点法式方程，平面内任意一点$M(x, y, z)$的坐标$x、y、z$均满足此方程。

---

平面的一般方程

易看出平面的点法式方程是一个三元一次方程，所以它也可以写成三元一次方程的一般形式：

$$Ax + By + Cz + D = 0$$

其中平面的法向量坐标即为$x、y、z$的系数

$$\overrightarrow n = (A, B, C)$$

对于平面的一般方程，可以从它的方程式中找到方程对应的图像的特点：

• $D = 0$是表示平面经过原点。
• $A = 0$时表示平面平行于$x$轴；$B = 0$时表示平面平行于$y$轴；$C = 0$时表示平面平行于$z$轴。(简记为：缺哪个未知数则经过哪个轴)
• $A = 0$且$D = 0$时表示平面经过$x$轴；$B = 0$时表示平面经过$y$轴；$C = 0$时表示平面经过$z$轴。
• $A = B = 0$时则平面同时经过$x$轴和$y$轴，即表示平面在$xOy$面上；$A = C = 0$时则平面同时经过$x$轴和$z$轴，即表示平面在$xOz$面上；$B = C = 0$时则平面同时经过$y$轴和$z$轴，即表示平面在$yOz$面上

---

平面的截距式方程

平面的截距式方程一般用于平面与$x、y、z$轴各有一个交点时，它的形式为：

$$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$$

截距式方程的推导：
一平面与$x、y、z$轴的交点依次为$P(a, 0, 0)，Q(0, b, 0)，R(0, 0, c)$三点

设该平面的方程为：

$$Ax + By + Cz + D= 0$$

分别将$P、Q、R$三点代入方程可得，即有：

$$\begin{cases} aA + D = 0\\ bB + D = 0\\ cC + D = 0\\ \end{cases}$$

解得：

$$A = -\frac{D}{a}，B = -\frac{D}{b}，C = -\frac{D}{c}$$

代入方程即可得截距式方程：

$$\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$$

---

两平面的夹角

两平面的夹角通常指的是两平面的法向量的夹角(锐角或者直角)

设两平面$\Pi_1、\Pi_2$的法向量分别为$n_1 = (A_1, B_1, C_1)、n_2 = (A_2, B_2, C_2)$，则：

$$\cos \theta= \frac{|A_1A_2 + B_1B_2 + C_1C_2|}{\sqrt{A_1^2 + B_1^2 + C_1^2}\sqrt{A_2^2 + B_2^2 + C_2^2}}$$ $$\theta = \arccos \frac{|A_1A_2 + B_1B_2 + C_1C_2|}{\sqrt{A_1^2 + B_1^2 + C_1^2}\sqrt{A_2^2 + B_2^2 + C_2^2}}$$

从两个法向量垂直、平行的充要条件可以推得：

• $\Pi_1 \bot \Pi_2(\theta = \frac{\pi}{2})$相当于$A_1A_2 + B_1B_2 + C_1C_2 = 0$
• $\Pi_1 // \Pi_2(\theta = \pi 或 0)$相当于$\frac{A_1}{A_2} = \frac{B_1}{B_2} = \frac{C_1}{C_2}$

---

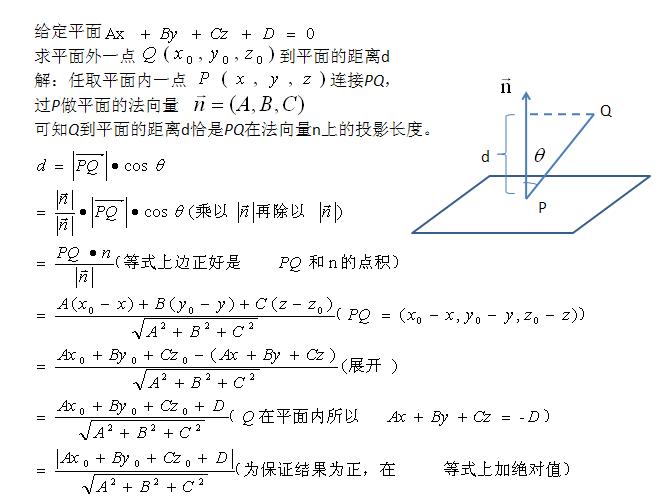
点到平面的距离

平面外一点$P_0(x_0, y_0, z_0)$到平面$Ax + By + Cz = 0$的距离公式：

$$d = \frac{|Ax_0 +By_0 +Cz_0|}{\sqrt{A^2 + B^2 + C^2}}$$