一、. 从损失函数公式本身来说
1. 从损失函数公式的物理含义来说
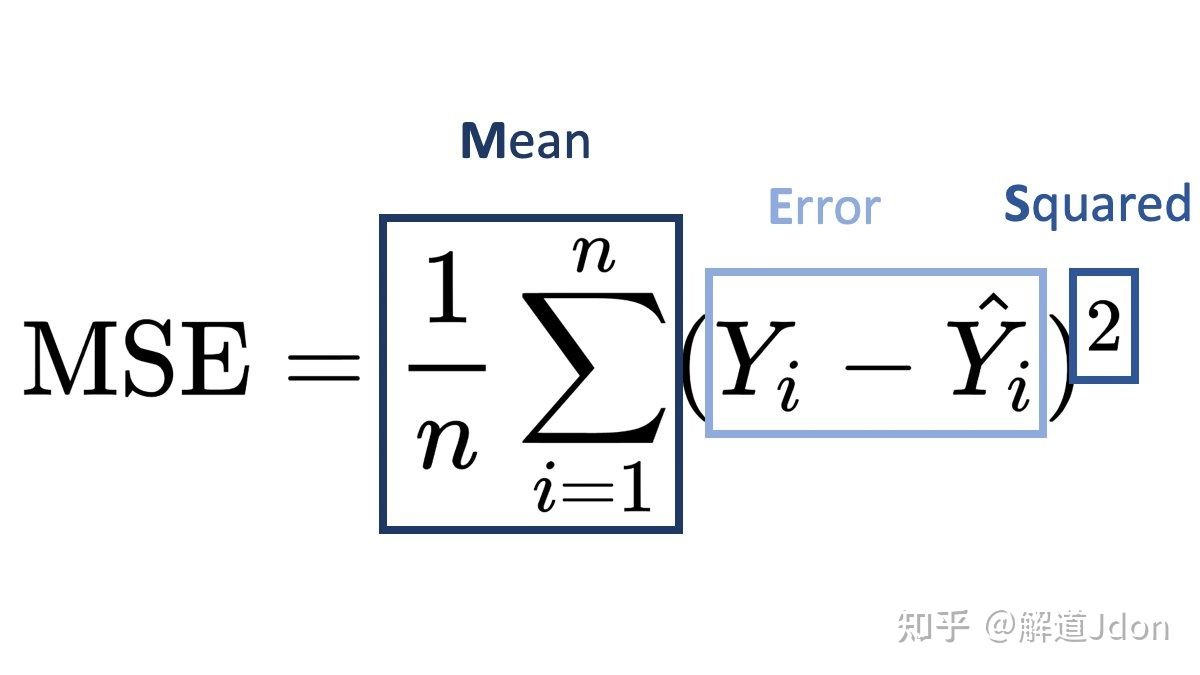
MSE衡量的是预测值和目标值的欧式距离。
而交叉熵是一个信息论的概念,交叉熵能够衡量同一个随机变量中的两个不同概率分布的差异程度,在机器学习中就表示为真实概率分布与预测概率分布之间的差异。交叉熵的值越小,模型预测效果就越好。
所以交叉熵本质上是概率问题,表征真实概率分布与预测概率分布差异,和几何上的欧氏距离无关,在回归中才有欧氏距离的说法,
而在分类问题中label的值大小在欧氏空间中是没有意义的。所以分类问题不能用mse作为损失函数。
2. 强行使用的话,可能带来的后果
MSE(均方误差)对于每一个输出的结果都非常看重(让正确分类变大的同时,也让错误分类变得平均),而交叉熵只对正确分类的结果看重。
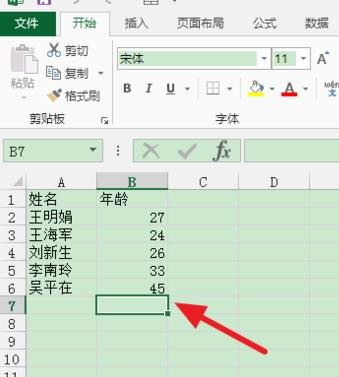
例如:在一个三分类模型中,模型的输出结果为(a,b,c),而真实的输出结果为(1,0,0),那么MSE与cross-entropy相对应的损失函数的值如下:
MSE: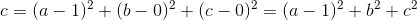
cross-entropy: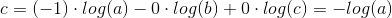
从上述的公式可以看出,交叉熵的损失函数只和分类正确的预测结果有关系,而MSE的损失函数还和错误的分类有关系,该分类函数除了让正确的分类尽量变大,还会让错误的分类变得平均,但实际在分类问题中这个调整是没有必要的。但是对于回归问题来说,这样的考虑就显得很重要了。所以,回归问题熵使用交叉上并不合适。
二、从优化求解角度来说
1. 非凸有多个极值点,不合适做损失函数
分类问题是逻辑回归,必须有激活函数这个非线性单元在,比如sigmoid(也可以是其他非线性激活函数),而如果还用mse做损失函数的话: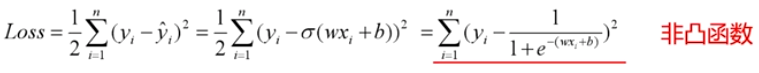
mse已经是非凸函数了,有多个极值点,所以不适用做损失函数了。
2.求解过程中可能梯度消失(不是主要原因)
mse作为损失函数,求导的时候都会有对激活函数的求导连乘运算,对于sigmoid、tanh,有很大区域导数为0的。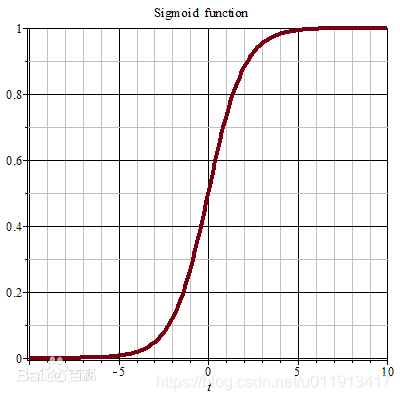
该激活函数的输入很可能直接就在平坦区域,那么导数就几乎是0,梯度就几乎不会被反向传递,梯度直接消失了。所以mse做损失函数的时候最后一层不能用sigmoid做激活函数,其他层可以用sigmoid做激活函数。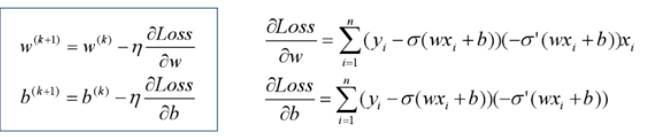
当然,用其他损失函数只能保证在第一步不会直接死掉,反向传播如果激活函数和归一化做得不好,同样会梯度消失。所以从梯度这个原因说mse不好不是很正确。

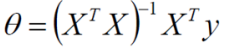
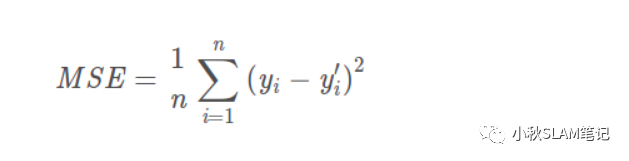

![已解决OSError: [WinError 6] 句柄无效。](https://img-blog.csdnimg.cn/a74f7d5d03234f7c8a635562034442a0.gif#pic_center)
![解决OSError: [Errno 98] Address already in use问题](https://img-blog.csdnimg.cn/445ad01aebb2478bb010a8093049ce42.png)

![报错OSError: [Errno 22] Invalid argument 的一种解决方法](https://img-blog.csdnimg.cn/412bf4cd5a204d69a52c7900d271e640.png)
![OSError[Errno 48]:Address already in use解决方法](https://img-blog.csdnimg.cn/20191227152238731.png)


![出现Python OSError: [Errno 22] Invalid argument的来龙去脉](https://img-blog.csdnimg.cn/d4cba45bc5cb463cbd7cd75ca32edee4.bmp?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA5r-A5Yqo55qE5YWU5a2Q,size_20,color_FFFFFF,t_70,g_se,x_16#pic_center)
![彻底解决 OSError: [WinError 127] 找不到指定的程序。](https://img-blog.csdnimg.cn/20210916145000755.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBAa2sxMjNr,size_20,color_FFFFFF,t_70,g_se,x_16)

![Python OSError: [Errno 22] Invalid argument:的出现和解决](https://img-blog.csdn.net/20180827093625299?watermark/2/text/aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3UwMTI1NjExNzY=/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70)