总结

1.口罩那题打完就只剩三十分钟了，之后卡在了完全二叉树的层序遍历那题，就没有再敢往后看，导致后面的网红打卡这道水题没做，去看前面的去了(某些丢了1、2分的这种题)，刚刚补题发现网红打卡这题就是很水很水的题。
2.很影响发挥的因素是比赛时眼睛很酸，天梯赛那天从1个小时开始眼睛就基本上睁不开了，不能看屏幕。最近看两个小时屏幕眼睛就开始难受，其实我觉得这才是最重要的因素导致我没有打好。但毕竟把这个当作原因给教练说就像是小学生作业没写找借口一样，我就没有说，然后被批了。
3.据说，2021年3、4月份，CCCC就又来了，关于树的原理和知识一定要弄懂，下次要做到看到这类题很开心的水平，下次一定会翻盘。

补题

L2-035 完全二叉树的层序遍历 (25分)

题目链接
题意：中文题，请直接去原网站看。

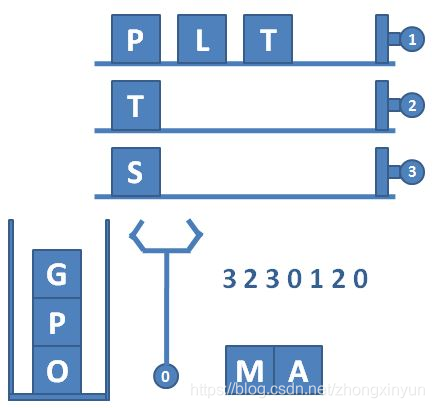
注意a数组是我们输入的数组，也就是题目给出的后序遍历的数组。我们这里不妨先把每个节点的值设为它的编号便于理解。tree数组是按照编号还原了这棵树，也就是实现了根据后序遍历来建树的目的。(tree[1]的值就是1号节点的值)
如图，根据我们的递归函数build，第一个被还原的是8号节点，且我们记录一个cnt来辅助还原，那么a[1]就是tree[8]的值。之后，第二个被还原的是tree[4]的值，它的值是a[2]。可以看到，a数组根据它的后序遍历给出了每个节点的值，我们就用tree数组来还原了这颗树。就像上述的那样，tree[8]就是a[1]，而a[1]本就应该是8号节点的值，那就对应上了。

int tree[33],a[33];
int cnt,n;void build(int id,int a[])
{if(id > n) return;build(id << 1,a);build(id << 1|1,a);tree[id] = a[++cnt];
}int main()
{cin >> n;rep(i,1,n) cin >> a[i];build(1,a);rep(i,1,n){cout << tree[i];if(i != n) cout << " ";}
}

L2-036 网红点打卡攻略 (25分)

题目链接
就是这道题，在我本来眼睛就很酸睁不开的时候给我来了这么一道贼长的水题。痛苦啊。
题意：请在上述链接看，中文题。
坑点只有一个，就是在它某个路线里面，可能num==n但是某个网红点打卡了多次，这样也是没满足要求的，这里用set去重判一下就满分了。
哦， 对了，n只有200，直接用邻接矩阵存图就行了。

const int N = 210;
int mp[N][N];int main()
{//freopen("in.txt","r",stdin);//freopen("out.txt","w",stdout);IOS;int n,m;cin >> n >> m;MEM(mp,-1);rep(i,1,m){int a,b,w;cin >> a >> b >> w;mp[a][b] = w;mp[b][a] = w;}int k;cin >> k;int ans = 0;int idx;int cost = INF;rep(o,1,k){int tcost = 0;int num;cin >> num;int t[210];set<int>pan;rep(i,1,num){cin >> t[i];pan.insert(t[i]);}if(num != n || pan.size() != n) continue;bool can = 1;rep(i,1,num-1){int c = mp[t[i]][t[i+1]];if(c == -1){can = 0;break;}tcost += mp[t[i]][t[i+1]];}int h1 = mp[0][t[1]], h2 = mp[t[num]][0];//    cout << "de: " << h2 << endl;if(h1 == -1 || h2 == -1)can = 0;if(!can) continue;tcost += (h1+h2);if(tcost < cost){cost = tcost;idx = o;}++ans;//    cout << "de: " << o << endl;}cout << ans << endl;cout << idx << " " << cost;
}

L3-025 那就别担心了 (30分)

题目链接
这题也是没看，实际上暴力搜索就能28分，拿满需要记忆化搜索。
思路：看代码，为什么else那里就能说一定不是逻辑自洽呢？因为如果连"所有的点收束到b"都满足不了，那么显然他们不可能收束到其他点，所以一定No。

28分版本：

const int N = 510;
int n,m;
vector<int>vec[510];
int a,b;
int cnt;
bool f = 1;
void dfs(int d)
{if(d == b){++cnt;return;}if(vec[d].size() != 0){for(auto i : vec[d]){dfs(i);}}else f = 0;
}int main()
{//freopen("in.txt","r",stdin);//freopen("out.txt","w",stdout);IOS;
//    int n,m;cin >> n >> m;while(m--){cin >> a >> b;vec[a].pb(b);}cin >> a >> b;dfs(a);cout << cnt << " " << (f == 0?"No":"Yes");
}

30分版本(记忆化搜索)

const int N = 510;
int n, m;
vector<int> vec[510];
int num[510]; //表示从idx这个点到目标点b的路径条数
int a, b;
int cnt;
bool f = 1;
void dfs(int d)
{num[d] = 0;//这里注意if (vec[d].size() != 0){for (auto i : vec[d]){if (num[i] == -1)//代表这个孩子还没有被算过，那就去算它dfs(i);num[d] += num[i];}}elsef = 0;
}int main()
{//freopen("in.txt","r",stdin);//freopen("out.txt","w",stdout);IOS;cin >> n >> m;MEM(num, -1);while (m--){cin >> a >> b;vec[a].pb(b);}cin >> a >> b;num[b] = 1;//这里初始化不要忘记!dfs(a);cout << num[a] << " " << (f == 0 ? "No" : "Yes");
}