本帖最后由 TS-boys 于 2020-10-30 13:29 编辑

1. 引子

面向对象编程是一种非常流行的编程思想，将“数据/属性”和“方法/函数”打包为对象，有利于大型软件的维护。基于这种思想，不同的编程语言，比如C++、JAVA等进行了不同的诠释。MATLAB也同样，对这种编程思想提供了支持，且有增加的趋势。

2. 基本的面向对象编程

2.1 创建一个对象

非常简单的创建方法，与新建函数或脚本一样，只是这里变成了新建 class。新建后会自动出现模板，在模板基础上修改即可。

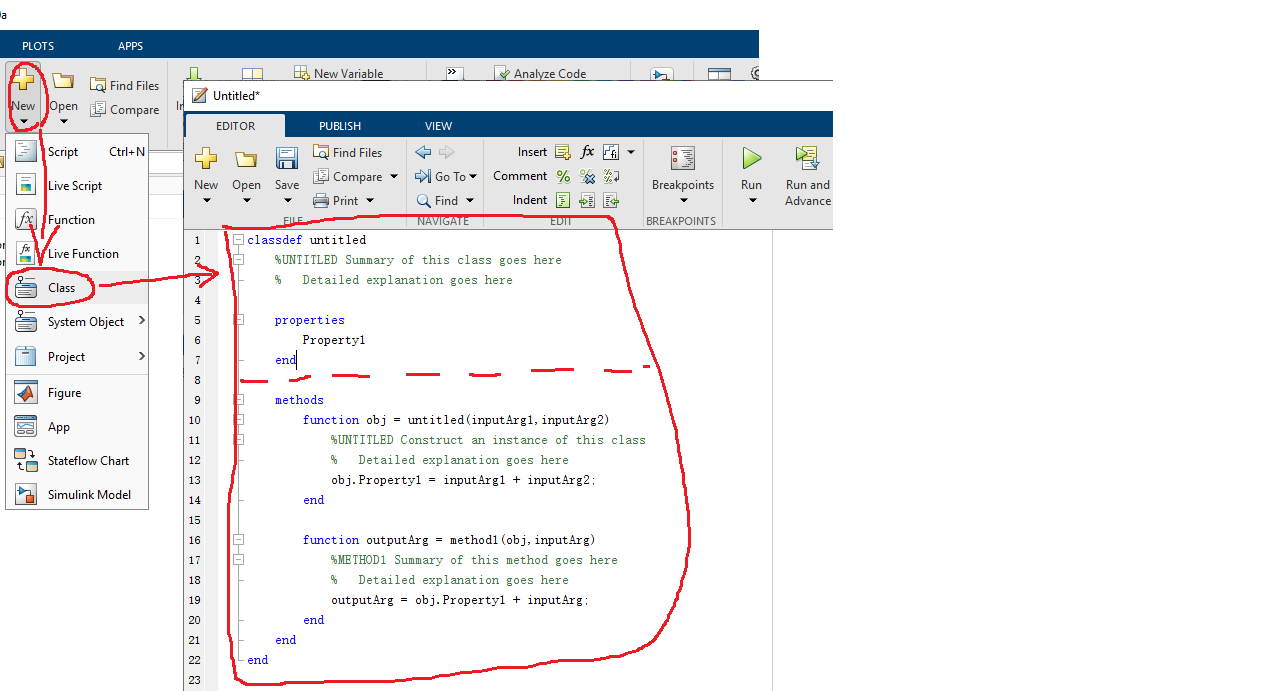
p1.png (68.78 KB, 下载次数: 18)

2020-10-30 13:16 上传

2.2 对象的定义

定义一个对象，自然要有名字，classdef 后就是对象的名字。一个合法的对象名字，与MATLAB变量规则相同，字母开头、区分大小写、不能用特殊字符，例如 student 就是一个合法的对象名字。修改后直接保存，就能得到一个同名的student.m 文件，一个对象就创建好了。

2.3 数据/属性

一个对象需要包含一定的数据或属性，例如“学生”作为一个对象，姓名、年龄、分数都可能是数据。在 MATLAB 中定义数据的关键字是 properties … end 配对，关键字之间定义多个属性名即可。同样，属性名的命