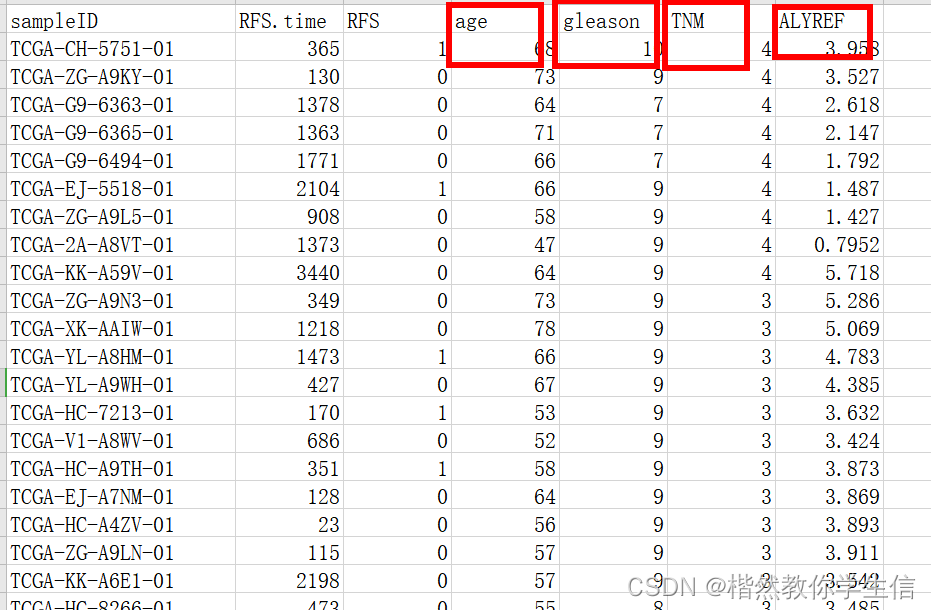
对连续性变量进行LASSO回归
jmzeng@163.com
6/19/2017
- 我的博客
- 我们的论坛
- 捐赠我
安装并加载必须的packages
如果你还没有安装,就运行下面的代码安装:
install.packages('lars')
install.packages('glmnet')如果你安装好了,就直接加载它们即可
library(lars)
# https://cran.r-project.org/web/packages/lars/lars.pdf
library(glmnet)
data(diabetes)首先查看测试数据的基本信息
这是一个糖尿病相关的数据集,包含两个x矩阵和一个y结果向量,分别是:
- x a matrix with 10 columns (自变量)
- y a numeric vector (因变量)
- x2 a matrix with 64 columns
attach(diabetes)
summary(x)## age sex bmi
## Min. :-0.107226 Min. :-0.04464 Min. :-0.090275
## 1st Qu.:-0.037299 1st Qu.:-0.04464 1st Qu.:-0.034229
## Median : 0.005383 Median :-0.04464 Median :-0.007284
## Mean : 0.000000 Mean : 0.00000 Mean : 0.000000
## 3rd Qu.: 0.038076 3rd Qu.: 0.05068 3rd Qu.: 0.031248
## Max. : 0.110727 Max. : 0.05068 Max. : 0.170555
## map tc ldl
## Min. :-0.112400 Min. :-0.126781 Min. :-0.115613
## 1st Qu.:-0.036656 1st Qu.:-0.034248 1st Qu.:-0.030358
## Median :-0.005671 Median :-0.004321 Median :-0.003819
## Mean : 0.000000 Mean : 0.000000 Mean : 0.000000
## 3rd Qu.: 0.035644 3rd Qu.: 0.028358 3rd Qu.: 0.029844
## Max. : 0.132044 Max. : 0.153914 Max. : 0.198788
## hdl tch ltg
## Min. :-0.102307 Min. :-0.076395 Min. :-0.126097
## 1st Qu.:-0.035117 1st Qu.:-0.039493 1st Qu.:-0.033249
## Median :-0.006584 Median :-0.002592 Median :-0.001948
## Mean : 0.000000 Mean : 0.000000 Mean : 0.000000
## 3rd Qu.: 0.029312 3rd Qu.: 0.034309 3rd Qu.: 0.032433
## Max. : 0.181179 Max. : 0.185234 Max. : 0.133599
## glu
## Min. :-0.137767
## 1st Qu.:-0.033179
## Median :-0.001078
## Mean : 0.000000
## 3rd Qu.: 0.027917
## Max. : 0.135612summary(y)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 25.0 87.0 140.5 152.1 211.5 346.0boxplot(y)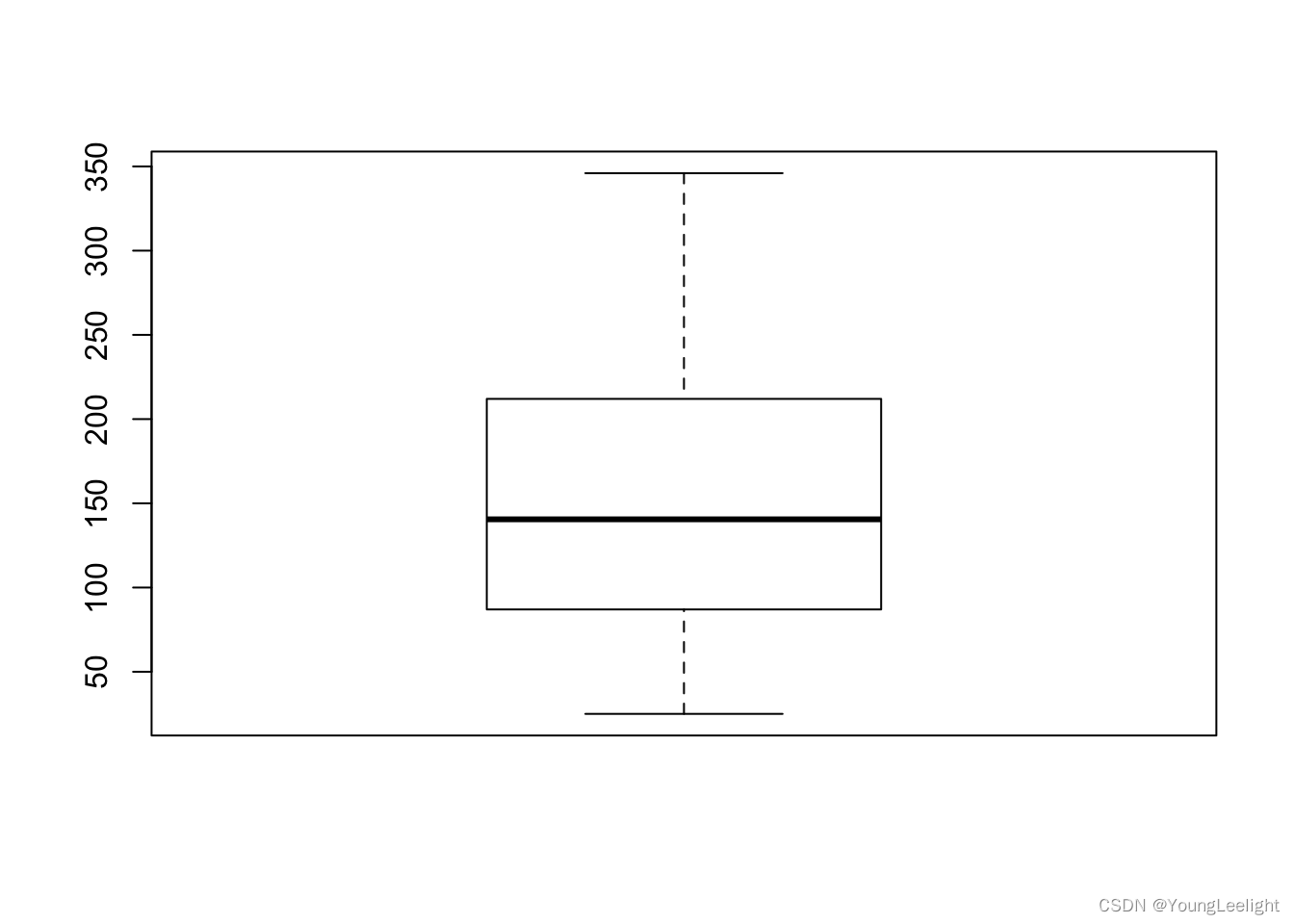
#summary(x2)其中x矩阵含有10个变量,分别是:“age” “sex” “bmi” “map” “tc” “ldl” “hdl” “tch” “ltg” “glu” 它们都在一定程度上或多或少的会影响个体糖尿病状态。
数据的详细介绍见 Efron, Hastie, Johnstone and Tibshirani (2003) “Least Angle Regression” (with discussion) Annals of Statistics;
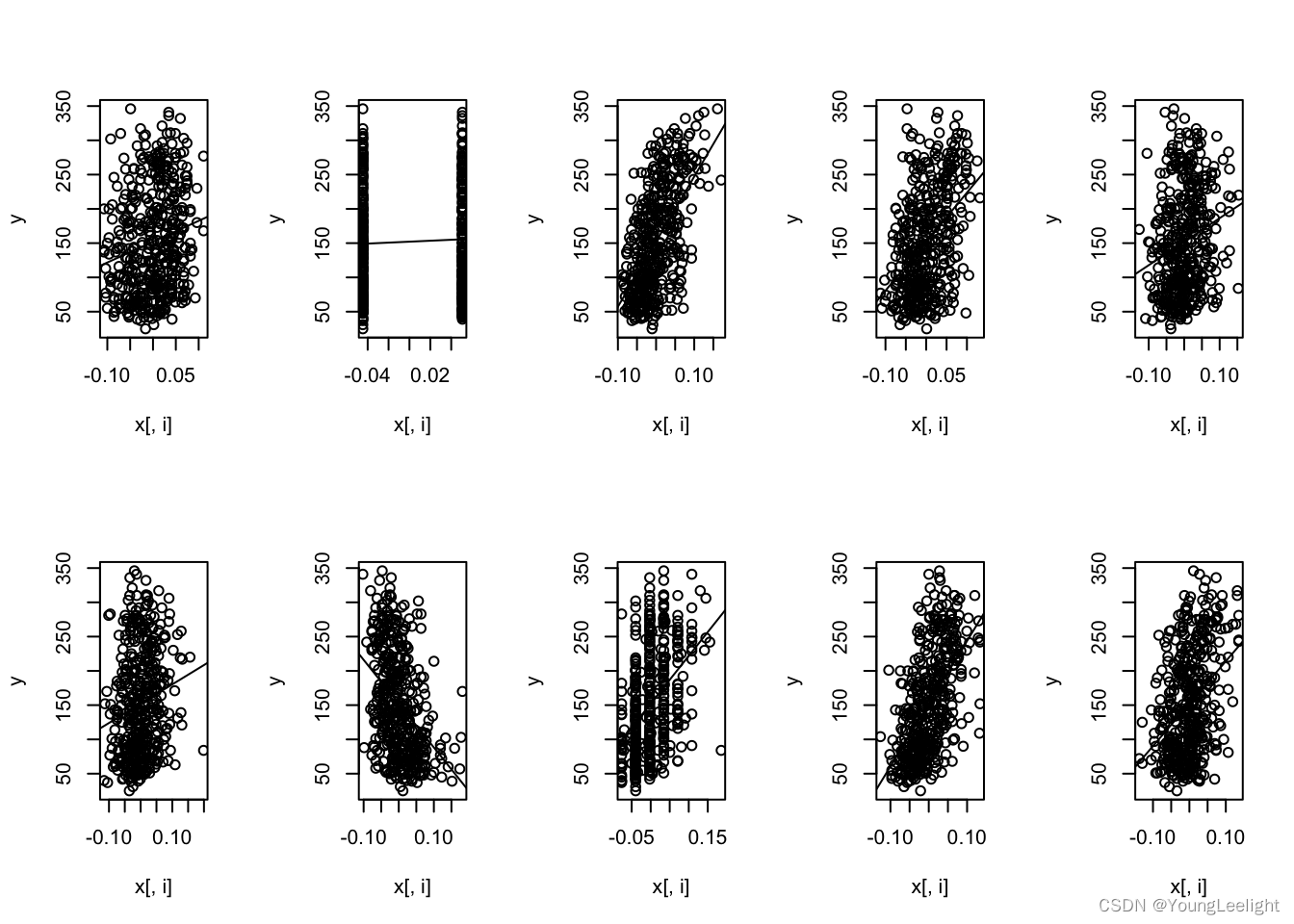
先看看因变量和每一个自变量的关系
oldpar=par()
par(mfrow=c(2,5))
for(i in 1:10){plot(x[,i], y)abline(lm(y~x[,i]))
}
par(oldpar)再对数据进行简单的线性回归
model_ols <- lm(y ~ x)
summary(model_ols)##
## Call:
## lm(formula = y ~ x)
##
## Residuals:
## Min 1Q Median 3Q Max
## -155.829 -38.534 -0.227 37.806 151.355
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 152.133 2.576 59.061 < 2e-16 ***
## xage -10.012 59.749 -0.168 0.867000
## xsex -239.819 61.222 -3.917 0.000104 ***
## xbmi 519.840 66.534 7.813 4.30e-14 ***
## xmap 324.390 65.422 4.958 1.02e-06 ***
## xtc -792.184 416.684 -1.901 0.057947 .
## xldl 476.746 339.035 1.406 0.160389
## xhdl 101.045 212.533 0.475 0.634721
## xtch 177.064 161.476 1.097 0.273456
## xltg 751.279 171.902 4.370 1.56e-05 ***
## xglu 67.625 65.984 1.025 0.305998
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 54.15 on 431 degrees of freedom
## Multiple R-squared: 0.5177, Adjusted R-squared: 0.5066
## F-statistic: 46.27 on 10 and 431 DF, p-value: < 2.2e-16可以看到,如果用普通的线性回归分析,有4个变量(bmi,sex,map,ltg),还有截距都显著影响着糖尿病.
接下来进行LASSO回归
很简单,一个命令即可。目前最好用的拟合广义线性模型的R package是glmnet,由LASSO回归的发明人,斯坦福统计学家Trevor Hastie领衔开发。它的特点是对一系列不同λ值进行拟合,每次拟合都用到上一个λ值拟合的结果,从而大大提高了运算效率。
model_lasso <- glmnet(x, y, family="gaussian", nlambda=50, alpha=1)参数family规定了回归模型的类型:
- family=“gaussian” 适用于一维连续因变量(univariate)
- family=“mgaussian” 适用于多维连续因变量(multivariate)
- family=“poisson” 适用于非负次数因变量(count)
- family=“binomial” 适用于二元离散因变量(binary)
- family=“multinomial” 适用于多元离散因变量(category)
参数nlambda=50让算法自动挑选50个不同的λ值,拟合出50个系数不同的模型。
参数alpha=1输入α值,1是它的默认值。参数α来控制应对高相关性(highly correlated)数据时模型的性状.
LASSO回归的结果解析
print(model_lasso)##
## Call: glmnet(x = x, y = y, family = "gaussian", alpha = 1, nlambda = 50)
##
## Df %Dev Lambda
## [1,] 0 0.0000 45.160000
## [2,] 2 0.1329 37.420000
## [3,] 2 0.2352 31.010000
## [4,] 2 0.3055 25.700000
## [5,] 3 0.3542 21.290000
## [6,] 3 0.3937 17.640000
## [7,] 4 0.4213 14.620000
## [8,] 4 0.4433 12.120000
## [9,] 4 0.4584 10.040000
## [10,] 4 0.4688 8.319000
## [11,] 4 0.4759 6.893000
## [12,] 5 0.4833 5.712000
## [13,] 5 0.4913 4.733000
## [14,] 6 0.4968 3.922000
## [15,] 7 0.5009 3.250000
## [16,] 7 0.5052 2.693000
## [17,] 7 0.5081 2.232000
## [18,] 7 0.5101 1.849000
## [19,] 7 0.5115 1.532000
## [20,] 7 0.5125 1.270000
## [21,] 7 0.5131 1.052000
## [22,] 8 0.5137 0.871900
## [23,] 8 0.5143 0.722500
## [24,] 8 0.5147 0.598700
## [25,] 8 0.5149 0.496100
## [26,] 8 0.5151 0.411100
## [27,] 8 0.5152 0.340600
## [28,] 8 0.5153 0.282300
## [29,] 10 0.5156 0.233900
## [30,] 10 0.5163 0.193800
## [31,] 10 0.5167 0.160600
## [32,] 10 0.5170 0.133100
## [33,] 10 0.5172 0.110300
## [34,] 10 0.5174 0.091390
## [35,] 9 0.5174 0.075730
## [36,] 9 0.5174 0.062750
## [37,] 10 0.5175 0.052000
## [38,] 10 0.5175 0.043090
## [39,] 10 0.5176 0.035700
## [40,] 10 0.5176 0.029590
## [41,] 10 0.5177 0.024520
## [42,] 10 0.5177 0.020310
## [43,] 10 0.5177 0.016830
## [44,] 10 0.5177 0.013950
## [45,] 10 0.5177 0.011560
## [46,] 10 0.5177 0.009578
## [47,] 10 0.5177 0.007937每一行代表了一个模型。
列Df是自由度,代表了非零的线性模型拟合系数的个数。
列%Dev代表了由模型解释的残差的比例,对于线性模型来说就是模型拟合的R^2(R-squred)。它在0和1之间,越接近1说明模型的表现越好,如果是0,说明模型的预测结果还不如直接把因变量的均值作为预测值来的有效。
列Lambda当然就是每个模型对应的λ值。
我们可以看到,随着λ的变小,越来越多的自变量被模型接纳进来,%Dev也越来越大。
第29行时,模型包含了所有20个自变量,%Dev也在0.5以上。
其实我们本应该得到50个不同的模型,但是连续几个%Dev变化很小时glmnet()会自动停止。
分析模型输出我们可以看到当Df大于9的时候,%Dev就达到了0.5,而且继续缩小λ,即增加更多的自变量到模型中,也不能显著提高%Dev。
所以我们可以认为当λ接近0.23时,得到的包含10个自变量的模型,已经是最好的描述这组数据的模型了。
我们也可以通过指定λ值,抓取出某一个模型的系数:
coef(model_lasso, s=c(model_lasso$lambda[29],0.23))## 11 x 2 sparse Matrix of class "dgCMatrix"
## 1 2
## (Intercept) 152.1334842 152.1334842
## age -0.1744351 -0.3396002
## sex -227.4412952 -227.6460806
## bmi 526.5411179 526.4325058
## map 315.1207791 315.2735154
## tc -227.5703945 -236.5240061
## ldl 26.5812439 33.7330891
## hdl -139.7688154 -135.9670209
## tch 109.4083069 110.4666063
## ltg 541.8941364 545.2162329
## glu 64.7035129 64.7539943作图观察LASSO回归模型的系数是如何变化的
plot.glmnet(model_lasso, xvar = "norm", label = TRUE)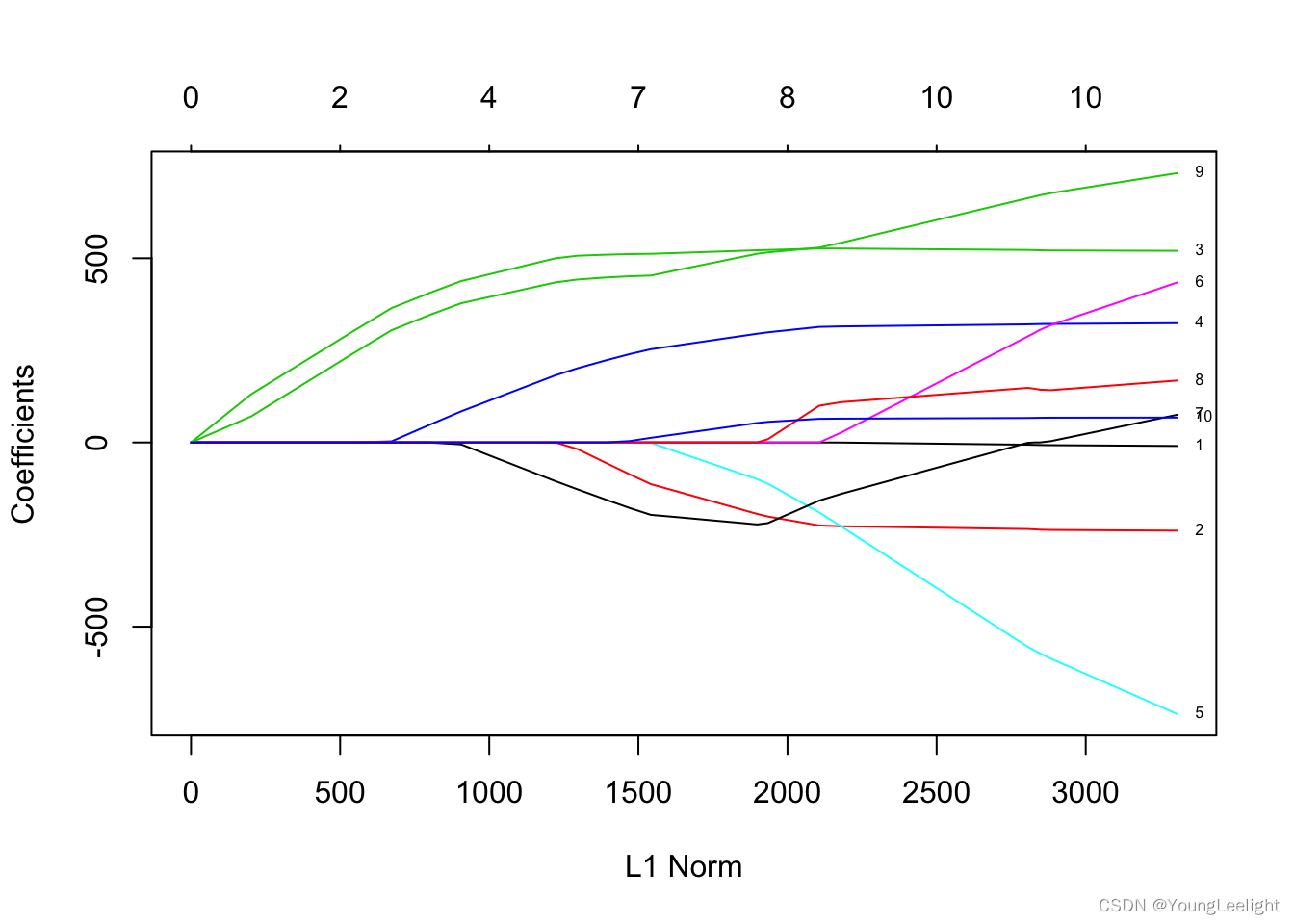
plot(model_lasso, xvar="lambda", label=TRUE)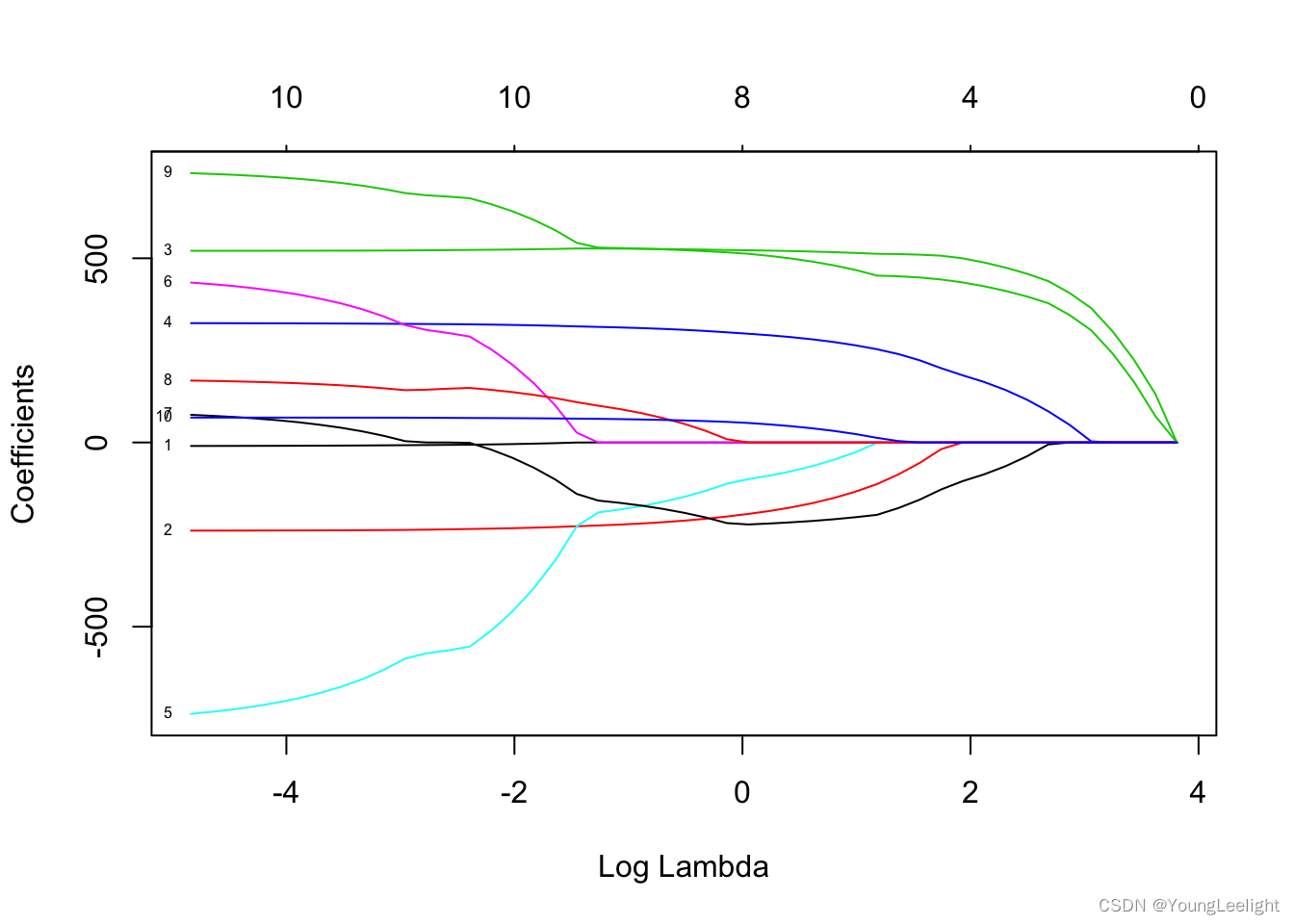
图中的每一条曲线代表了每一个自变量系数的变化轨迹,纵坐标是系数的值,下横坐标是loga(λ),上横坐标是此时模型中非零系数的个数。我们可以看到,黑线代表的自变量1在λ值很大时就有非零的系数,然后随着λ值变小不断变大。我们还可以尝试用xvar=“norm”和xvar=“dev”切换下横坐标。
用自带glmnet()函数模型进行预测
pre <- predict(model_lasso, newx=x , s=c(model_lasso$lambda[29],0.23))
head(cbind(y,pre))## y 1 2
## [1,] 151 204.54545 204.56986
## [2,] 75 70.58607 70.54513
## [3,] 141 175.79128 175.80730
## [4,] 206 163.01751 163.08081
## [5,] 135 127.76397 127.77541
## [6,] 97 105.66422 105.67519用交叉验证来确定最优lambda值
公式中的lambda是重要的设置参数,它控制了惩罚的严厉程度,如果设置得过大,那么最后的模型参数均将趋于0,形成拟合不足。如果设置得过小,又会形成拟合过度。所以lambda的取值一般需要通过交叉检验来确定。这时候需要用lars包的glmnet()函数啦!
cv_fit <- cv.glmnet(x=x, y=y, alpha = 1, nlambda = 1000)参数nlambda=1000让算法自动挑选1000个不同的λ值,拟合出1000个系数不同的模型。
其实cv.glmnet()函数的参数值得注意的还有两个,其中type.measure是用来指定交叉验证选取模型时希望最小化的目标参量。
还可以用nfolds指定fold数,或者用foldid指定每个fold的内容。
可视化交叉验证结果
plot.cv.glmnet(cv_fit)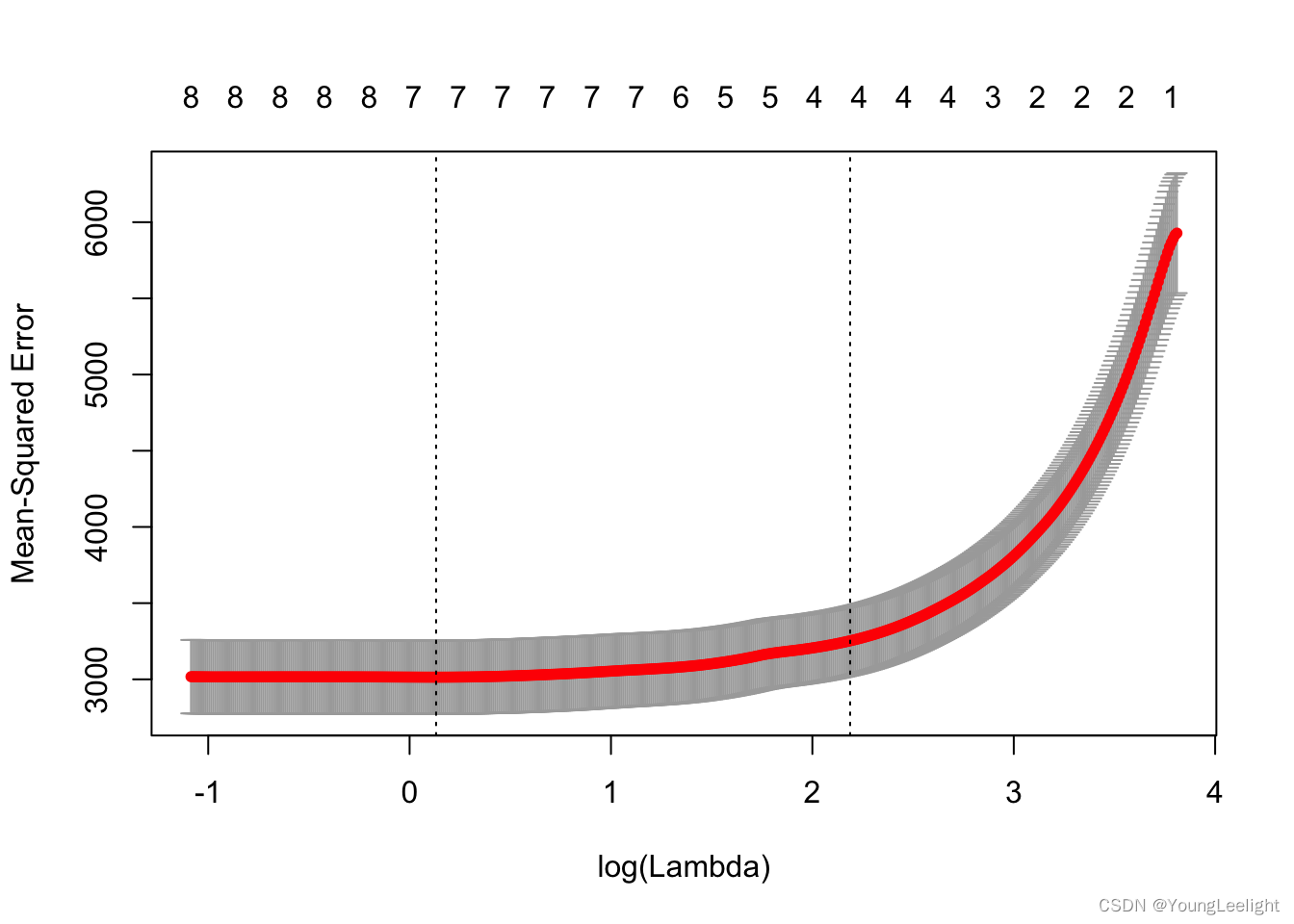
因为交叉验证,对于每一个λ值,在红点所示目标参量的均值左右,我们可以得到一个目标参量的置信区间。两条虚线分别指示了两个特殊的λ值:
c(cv_fit$lambda.min,cv_fit$lambda.1se)## [1] 1.140661 8.913526lambda.min是指在所有的λ值中,得到最小目标参量均值的那一个。
而lambda.1se是指在lambda.min一个方差范围内得到最简单模型的那一个λ值。
因为λ值到达一定大小之后,继续增加模型自变量个数即缩小λ值,并不能很显著的提高模型性能,lambda.1se给出的就是一个具备优良性能但是自变量个数最少的模型。
用cv.glmnet()函数模型进行预测
pre <- predict(cv_fit, newx=x[1:5,], type="response", s="lambda.1se")
head(cbind(y,pre))## Warning in cbind(y, pre): number of rows of result is not a multiple of
## vector length (arg 1)## y 1
## [1,] 151 197.19236
## [2,] 75 88.54846
## [3,] 141 176.50576
## [4,] 206 153.14809
## [5,] 135 123.88797提取模型的系数
cv_fit$lambda.min## [1] 1.140661fit <- glmnet(x=x, y=y, alpha = 1, lambda=cv_fit$lambda.min)
fit$beta## 10 x 1 sparse Matrix of class "dgCMatrix"
## s0
## age .
## sex -190.88636
## bmi 521.26169
## map 293.55728
## tc -95.35910
## ldl .
## hdl -221.79409
## tch .
## ltg 509.63138
## glu 51.29918coef(cv_fit$glmnet.fit, s = min(cv_fit$lambda))## 11 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 152.13348
## age .
## sex -222.99096
## bmi 526.27917
## map 312.40981
## tc -183.52085
## ldl .
## hdl -162.22910
## tch 92.59096
## ltg 528.00455
## glu 63.40113cv_fit$lambda.1se## [1] 8.913526fit <- glmnet(x=x, y=y, alpha = 1, lambda=cv_fit$lambda.1se)
fit$beta## 10 x 1 sparse Matrix of class "dgCMatrix"
## s0
## age .
## sex .
## bmi 483.8524
## map 156.7522
## tc .
## ldl .
## hdl -78.9380
## tch .
## ltg 419.7262
## glu .coef(cv_fit$glmnet.fit, s = cv_fit$lambda.1se)## 11 x 1 sparse Matrix of class "dgCMatrix"
## 1
## (Intercept) 152.13348
## age .
## sex .
## bmi 483.78833
## map 156.74421
## tc .
## ldl .
## hdl -78.93562
## tch .
## ltg 419.75889
## glu .因为每个fold间的计算是独立的。 我们还可以考虑运用并行计算来提高运算效率,使用parallel=TRUE可以开启这个功能。但是我们需要先装载package doParallel。
可以用并行加快计算速度
并行的示例代码是:
library(doParallel)
# Windows System
cl <- makeCluster(6)
registerDoParallel(cl)
cvfit = cv.glmnet(x, y, family = "binomial", type.measure = "class", parallel=TRUE)
stopCluster(cl)
# Linux System
registerDoParallel(cores=8)
cvfit = cv.glmnet(x, y, family = "binomial", type.measure = "class", parallel=TRUE)
stopImplicitCluster()用model.matrix函数把自变量的离散变量变成矩阵输入
LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选(Variable Selection)和复杂度调整(Regularization)。因此,不论目标因变量(dependent/response varaible)是连续的(continuous),还是二元或者多元离散的(discrete), 都可以用LASSO回归建模然后预测。
但是,glmnet只能接受数值矩阵作为模型输入,如果自变量中有离散变量的话,需要把这一列离散变量转化为几列只含有0和1的向量,这个过程叫做One Hot Encoding。
下面是一个例子
df=data.frame(Factor=factor(1:5), Character=c("a","a","b","b","c"),Logical=c(T,F,T,T,T), Numeric=c(2.1,2.3,2.5,4.1,1.1))
model.matrix(~., df)## (Intercept) Factor2 Factor3 Factor4 Factor5 Characterb Characterc
## 1 1 0 0 0 0 0 0
## 2 1 1 0 0 0 0 0
## 3 1 0 1 0 0 1 0
## 4 1 0 0 1 0 1 0
## 5 1 0 0 0 1 0 1
## LogicalTRUE Numeric
## 1 1 2.1
## 2 0 2.3
## 3 1 2.5
## 4 1 4.1
## 5 1 1.1
## attr(,"assign")
## [1] 0 1 1 1 1 2 2 3 4
## attr(,"contrasts")
## attr(,"contrasts")$Factor
## [1] "contr.treatment"
##
## attr(,"contrasts")$Character
## [1] "contr.treatment"
##
## attr(,"contrasts")$Logical
## [1] "contr.treatment"除此之外,如果我们想让模型的变量系数都在同一个数量级上,就需要在拟合前对数据的每一列进行标准化(standardize),即对每个列元素减去这一列的均值然后除以这一列的标准差。这一过程可以通过在glmnet()函数中添加参数standardize=TRUE来实现。
模型其它技巧
指定模型系数的上限与下限
使用upper.limits和lower.limits,上限与下限可以是一个值,也可以是一个向量,向量的每一个值作为对应自变量的参数上下限。
调整惩罚参数
有时,在建模之前我们就想凸显某几个自变量的作用,此时我们可以调整惩罚参数,即设置penalty.factor。每个自变量的默认惩罚参数是1,把其中的某几个量设为0将使得相应的自变量不遭受任何惩罚