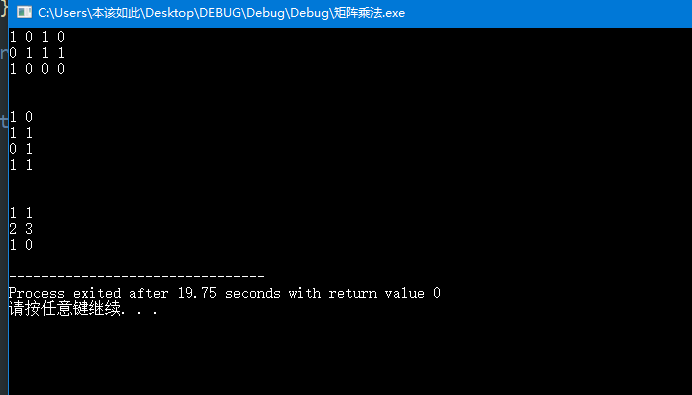
利用矩阵的逆（伪逆）与除法求解：

对于线性方程组Ax=b，若其为恰定方程组且A是非奇异的，则求x最明显的方法便是利用矩阵的逆，即x=A\b;若不是恰定方程组，则可利用伪逆来求其一个特解。

运用pinv命令求伪逆：

format rat %表示以有理数形式输出结果
A=[1,2,2,0;0,1,-2,-2;1,3,0,-2]
b=[1,2,3]' %'表示矩阵转置。当矩阵为复数时，求矩阵的共轭转置
x0=pinv(A)*b
Z=null(A,'r')

实例——矩阵特征值

演示求逆法与除法求解线性方程组在时间与精度上的区别

（tic和toc用来记录matlab命令执行的时间。tic用来保存当前时间，而后使用toc来记录程序完成时间。 两者往往结合使用）

（对矩阵求逆。如果A是非奇异方阵，则B/A = B*inv(A)，A\B = inv(A)*B。/表示右除，\表示左除）。

注意：使用inv时，必须对象为方阵。

A=1000*rand(1000,1000);
x=ones(1000,1);
b=A*x;
disp('利用矩阵的逆求解所用时间及误差为：')
tic %tic和toc用来记录matlab命令执行的时间。tic用来保存当前时间，而后使用toc来记录程序完成时间。 两 %者往往结合使用
y=inv(A)*b;%对矩阵求逆。如果A是非奇异方阵，则B/A = B*inv(A)，A\B = inv(A)*B。/表示右除，\表示左 %除
t1=toc
error1=norm(y-x)
disp('利用除法求解所用时间及误差为：')
tic
y=A\b;
t2=toc
error2=norm(y-x)