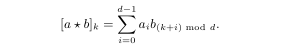文章目录
- 多因子与对比分析可视化
- 理论基础
- 假设检验与方差检验
- 假设检验
- 方差检验
- 相关系数:皮尔逊、斯皮尔曼
- 回归:线性回归
- PCA与奇异值分解
- 代码实践
- 交叉分析
- 分组分析
- 相关分析
- 因子分析
- 总结
- 代码实现
- 相关性
- 线性回归
- PCA
- 注意:sklearn中pca用的方法是奇异值分解的方法,并不是pc方法,下面用pc方法实现
- 交叉分析
- 分组与钻取
- 相关分析
- 条件熵
- 熵增益
- 衡量离散值的相关性
- 基尼系数
- 因子分析
数据分析全过程梳理见
【数据分析入门】python数据分析全过程梳理
多因子与对比分析可视化
目的:展现数据全貌
理论基础
假设检验与方差检验
假设检验
根据一定的假设条件,从样本推断总体,或者推断样本与样本之间关系的一种方法。
根据样本已知的分布性质来推断整体的性质
假设检验的基本思想是“小概率事件”原理,其统计推断方法是带有某种概率性质的反证法。小概率思想是指小概率事件在一次试验中基本上不会发生。反证法思想是先提出检验假设,再用适当的统计方法,利用小概率原理,确定假设是否成立。即为了检验一个假设H0是否正确,首先假定该假设H0正确,然后根据样本对假设H0做出接受或拒绝的决策。如果样本观察值导致了“小概率事件”发生,就应拒绝假设H1,否则应接受假设H1。
假设检验的步骤:
显著性水平越低,要求越高

检验统计量:
t分布,样本区别
f检验,方差分析
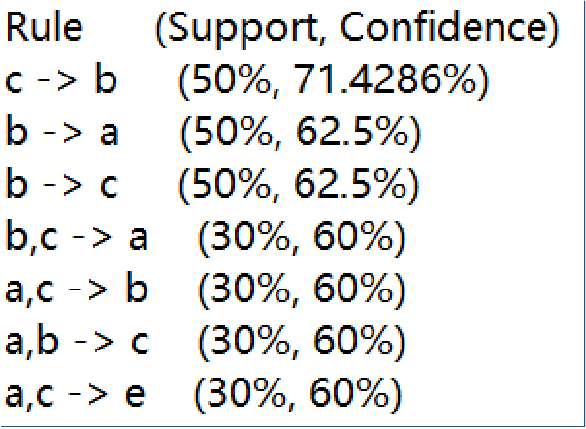
卡方检验,四格表检验法,检验两个指标有没有相关性
方差检验
F检验

R5piv5rip5biF5biF,size_17,color_FFFFFF,t_70,g_se,x_16)
独立分布t检验
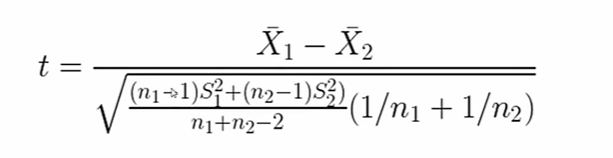
样本长度可以不一样
相关系数:皮尔逊、斯皮尔曼
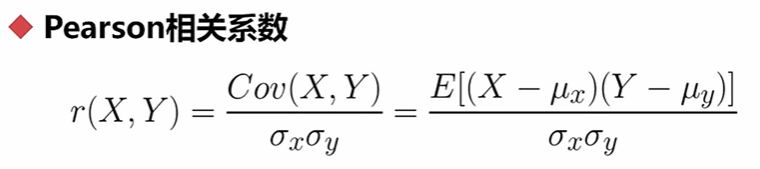
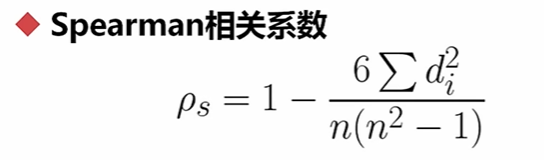
n是样本个数
d是排序
只跟相对大小有关
应用于相对比较的情况
回归:线性回归


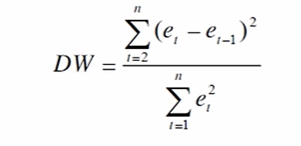
好的回归,DW值接近2,应该是残差不相关
PCA与奇异值分解

主成分最大的作用:降维
奇异值分解
代码实践
交叉分析
分组分析
相关分析
因子分析


总结

代码实现
相关性
import pandas as pd
s1=pd.Series([0.1,0.2,1.1,2.4,1.3,0.3,0.5])
s2=pd.Series([0.5,0.4,1.2,2.5,1.1,0.7,0.1])
s1.corr(s2)
0.9333729600465923
s1.corr(s2,method="spearman")
0.7142857142857144
df=pd.DataFrame([s1,s2])
df.corr()
df=pd.DataFrame(np.array([s1,s2]).T)
df.corr()
x=np.arange(10).astype(np.float).reshape((10,1))
C:\ProgramData\Miniconda3\lib\site-packages\ipykernel_launcher.py:1: DeprecationWarning: `np.float` is a deprecated alias for the builtin `float`. To silence this warning, use `float` by itself. Doing this will not modify any behavior and is safe. If you specifically wanted the numpy scalar type, use `np.float64` here.
Deprecated in NumPy 1.20; for more details and guidance: https://numpy.org/devdocs/release/1.20.0-notes.html#deprecations"""Entry point for launching an IPython kernel.
y=x*3+4+np.random.random((10,1))
线性回归
from sklearn.linear_model import LinearRegression
reg=LinearRegression()
res=reg.fit(x,y)
y_pred=reg.predict(x)
reg.coef_
array([[2.93514572]])
reg.intercept_
array([4.70737715])
PCA
data=np.array([np.array([2.5,0.5,2.2, 1.9,3.1,2.3,2, 1,1.5,1.1]),
np.array([2.4,0.7,2.9,2.2,3,2.7,1.6,1.1, 1.6,0.9])]).T
data
array([[2.5, 2.4],[0.5, 0.7],[2.2, 2.9],[1.9, 2.2],[3.1, 3. ],[2.3, 2.7],[2. , 1.6],[1. , 1.1],[1.5, 1.6],[1.1, 0.9]])
from sklearn.decomposition import PCAlower_dim=PCA(n_components=1)
lower_dim.fit(data)
PCA(n_components=1)
lower_dim.explained_variance_ratio_
array([0.96318131])
lower_dim.fit_transform(data)
array([[-0.82797019],[ 1.77758033],[-0.99219749],[-0.27421042],[-1.67580142],[-0.9129491 ],[ 0.09910944],[ 1.14457216],[ 0.43804614],[ 1.22382056]])
注意:sklearn中pca用的方法是奇异值分解的方法,并不是pc方法,下面用pc方法实现
import numpy as np
import pandas as pd
def myPCA(data,n_components=10000000):mean_value=np.mean(data,axis=0)mid=data-mean_valuecov_mat=np.cov(mid,rowvar=False)from scipy import linalgeig_vals,eig_vects=linalg.eig(np.mat(cov_mat))eig_val_index=np.argsort(eig_vals)eig_val_index=eig_val_index[:-(n_components+1):-1]eig_vects=eig_vects[:,eig_val_index]low_dim_mat=np.dot(mid,eig_vects)return low_dim_mat,eig_vals
myPCA(data,n_components=1)
交叉分析
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as snsdf=pd.read_csv('C:\\Users\\wenxiaoyu_intern\\Documents\\client_rfm.csv')
df=df.fillna(0)
df.loc[df['gain'] >0,['gain_type']]=1
df.loc[df['gain'] <=0,['gain_type']]=-1
df_indices=df.groupby(by="risk").indicess_values=df["vol"].iloc[df_indices[3]].values
l_values=df["vol"].iloc[df_indices[1]].values
ss.ttest_ind(s_values,l_values)[1]
0.1287748887778182
#颜色越深,越有关系
risk_keys=list(df_indices.keys())
dp_t_mat=np.zeros([len(risk_keys),len(risk_keys)])
for i in range(len(risk_keys)):for j in range(len(risk_keys)):p_value=ss.ttest_ind(df["vol"].iloc[df_indices[risk_keys[i]]].values,df["vol"].iloc[df_indices[risk_keys[j]]].values)[1]if p_value <0.05:dp_t_mat[i][j]=-1else:dp_t_mat[i][j]=p_value
sns.heatmap(dp_t_mat,xticklabels=risk_keys,yticklabels=risk_keys)
<AxesSubplot:>
#颜色越深,没有关系,颜色越浅,越有关系
risk_keys=list(df_indices.keys())
dp_t_mat=np.zeros([len(risk_keys),len(risk_keys)])
for i in range(len(risk_keys)):for j in range(len(risk_keys)):p_value=ss.ttest_ind(df["gain_type"].iloc[df_indices[risk_keys[i]]].values,df["gain_type"].iloc[df_indices[risk_keys[j]]].values)[1]dp_t_mat[i][j]=p_value
sns.heatmap(dp_t_mat,xticklabels=risk_keys,yticklabels=risk_keys)
<AxesSubplot:>
#颜色越深,没有关系,颜色越浅,越有关系
risk_keys=list(df_indices.keys())
dp_t_mat=np.zeros([len(risk_keys),len(risk_keys)])
for i in range(len(risk_keys)):for j in range(len(risk_keys)):p_value=ss.ttest_ind(df["date_nums"].iloc[df_indices[risk_keys[i]]].values,df["date_nums"].iloc[df_indices[risk_keys[j]]].values)[1]dp_t_mat[i][j]=p_value
sns.heatmap(dp_t_mat,xticklabels=risk_keys,yticklabels=risk_keys)
<AxesSubplot:>
#透视表,交叉分析
piv_tb=pd.pivot_table(df,values="gain",index=["risk"],columns=["gain_type"],aggfunc=np.mean)
piv_tb
#透视表,交叉分析
piv_tb=pd.pivot_table(df,values="vol",index=["risk"],columns=["gain_type"],aggfunc=np.mean)
piv_tb
#透视表,交叉分析
piv_tb=pd.pivot_table(df,values="total_amount",index=["risk"],columns=["gain_type"],aggfunc=np.mean)
piv_tb
sns.heatmap(piv_tb)
#颜色越浅,交易量越大
<AxesSubplot:xlabel='gain_type', ylabel='risk'>
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-As1F1Kgr-1659436077451)(client_files/client_138_1.png)]
sns.heatmap(piv_tb,cmap=sns.color_palette(("Reds")))
#颜色越深,交易量越大
<AxesSubplot:xlabel='gain_type', ylabel='risk'>
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6LyZC4qp-1659436077452)(client_files/client_139_1.png)]
分组与钻取
sns.barplot(x="gain_type",y="vol",hue="risk",data=df)
<AxesSubplot:xlabel='gain_type', ylabel='vol'>
d_n=df["date_nums"]
sns.barplot(list(range(len(d_n))),d_n.sort_values())
C:\ProgramData\Miniconda3\lib\site-packages\seaborn\_decorators.py:43: FutureWarning: Pass the following variables as keyword args: x, y. From version 0.12, the only valid positional argument will be `data`, and passing other arguments without an explicit keyword will result in an error or misinterpretation.FutureWarning
相关分析
sns.heatmap(df.corr(),vmin=-1,vmax=1,cmap=sns.color_palette("RaBu",n_colors=128))
import pandas as pd
import numpy as np
s1=pd.Series(["X1","X1","X2","X2","X2","X2"])
s2=pd.Series(["Y1","Y1","Y1","Y2","Y2","Y2"])
s1.groupby(by=s1).count().values
array([2, 4], dtype=int64)
def getEntropy(s):#计算分布if not isinstance(s,pd.Series):s=pd.Series(s)prt_ary=s.groupby(by=s).count().values/float(len(s))return -(np.log2(prt_ary)*prt_ary).sum()
getEntropy(s1)#s1的熵,log2(2/6)*2/6+log2(4/6)*4
0.9182958340544896
getEntropy(s2)
1.0
条件熵
条件熵是不对称的
def getCondEntropy(s1,s2):d=dict()for i in list(range(len(s1))):d[s1[i]]=d.get(s1[i],[])+[s2[i]]return sum([getEntropy(d[k])*len(d[k])/float(len(s1)) for k in d])
getCondEntropy(s1,s2)
0.5408520829727552
getCondEntropy(s2,s1)
0.4591479170272448
熵增益
熵增益是对称的
熵增益率不是对称的
def getEntropyGain(s1,s2):return getEntropy(s2)-getCondEntropy(s1,s2)
def getEntropyGainRatio(s1,s2):return getEntropyGain(s1,s2)/getEntropy(s2)
getEntropyGain(s1,s2)
0.4591479170272448
getEntropyGain(s2,s1)
0.4591479170272448
getEntropyGainRatio(s1,s2)
0.4591479170272448
getEntropyGainRatio(s2,s1)
0.5
衡量离散值的相关性
import math
def getDiscreleCorr(s1,s2):return getEntropyGain(s1,s2)/math.sqrt(getEntropy(s1)*getEntropy(s2))getDiscreleCorr(s1,s2)
0.4791387674918639
getDiscreleCorr(s2,s1)
0.4791387674918639
基尼系数
#概率平方和
def getProbSS(s):#计算分布if not isinstance(s,pd.Series):s=pd.Series(s)prt_ary=s.groupby(by=s).count().values/float(len(s))return sum(prt_ary**2)def getGini(s1,s2):d=dict()for i in list(range(len(s1))):d[s1[i]]=d.get(s1[i],[])+[s2[i]]return 1-sum([getProbSS(d[k])*len(d[k])/float(len(s1)) for k in d]) getGini(s1,s2)
0.25
getGini(s2,s1)
0.2222222222222222
df=pd.read_csv(r"C:\Users\wenxiaoyu_intern\Documents\用户画像\client_rfm.csv")
df=df.fillna(0)
因子分析
主成分分析
from sklearn.decomposition import PCA
my_pca=PCA(n_components=7)
my_pca.fit_transform(df.drop(labels=["client_rfm"],axis=1))
df.drop(labels=["client_rfm"],axis=1)
lower_mat=my_pca.explained_variance_ratio_
import seaborn as sns
sns.heatmap(pd.DataFrame(lower_mat).corr(),vmin=1,vmax=1,cmap=sns.color_palette("RdBu"))