文章目录
- 1. 评估算法的效果
- 2. 方差(Variance)
- 2.1 总体方差
- 2.1.1 在numpy中计算总体方差
- 2.1.2 在pandas中计算总体方差
- 2.2 样本方差
- 2.2.1 在numpy中计算样本方差
- 2.2.2 在pandas中计算样本方差
- 3. 标准差 / 均方差 (Standard Deviation)
- 3.1 总体标准差
- 3.1.1 在numpy中计算总体标准差
- 3.1.2 在pandas中计算总体标准差
- 3.2 样本标准差
- 3.2.1 在numpy中计算样本标准差
- 3.2.2 在pandas中计算样本标准差
- 4. 均方误差(mean-square error, MSE)
- 5. 标准误差 / 均方根误差(root mean squared error,RMSE)
- 6. 所有值的计算方法汇总
1. 评估算法的效果
常见的算法效果评估函数是标准误差,亦称为:均方根误差(Root Mean Square Error),由于这个值的计算与方差,标准差,均方误差都有一定的关系,我们先通过下图给出它们之间的关系,然后逐一解释一下。
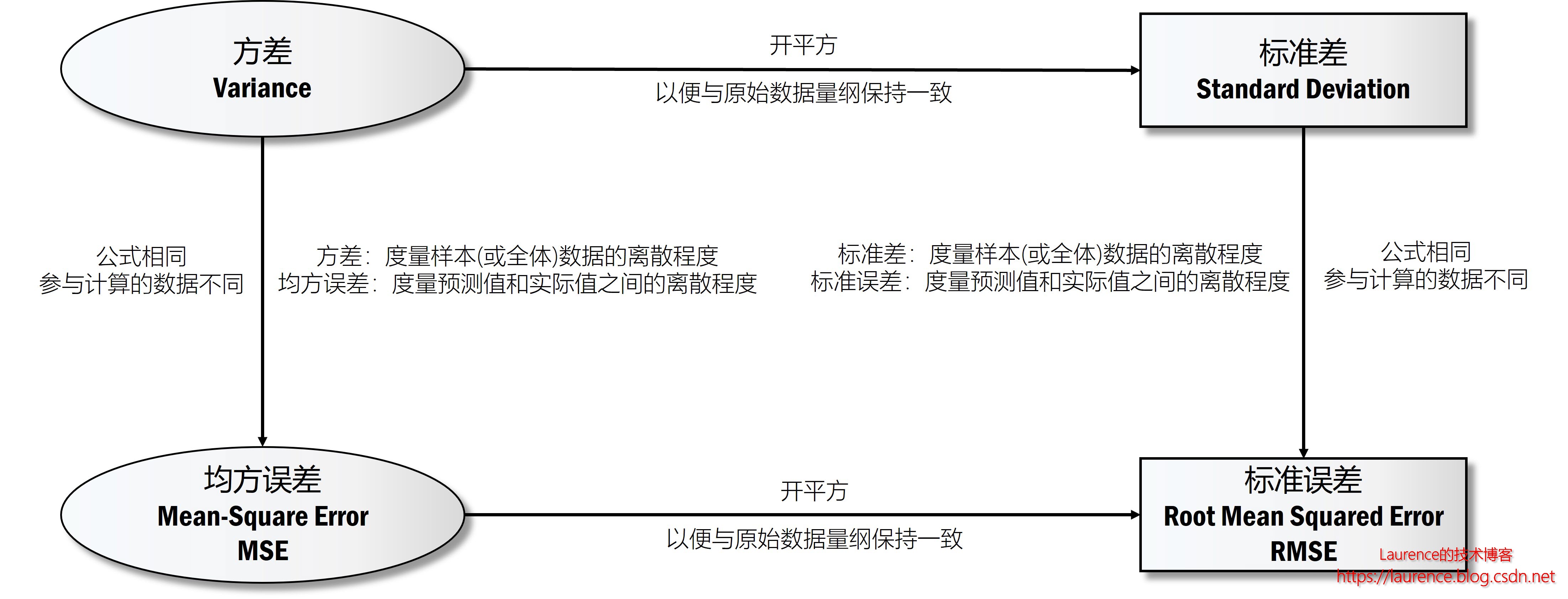
注:这份比较隐去了总体方差和样本方差之间的差异,统一用方差来指代了。
2. 方差(Variance)
方差用于度量一组数据的离散程度。对于方差我们可以用一种朴素的方式理解和记忆:它不是平方的差,而是差的平方求和之后再取平均值,对于计算方差取差的平方这一点,可以很形象地理解为以两点间的直线距离为边得到一个正方型,以面积(平方)的形式度量离散程度,显然面积越大,意味着离散程度越高。
2.1 总体方差
总体方差,也叫做有偏估计,其实就是普遍在使用的标准“方差”的概念。计算总体方差需要先计算出总体均值,总体均值的计算方式是:
总体均值:

其中,n表示这组数据个数,x1、x2、x3……xn表示这组数据具体数值。然后,基于总体均值,可得:
总体方差:

2.1.1 在numpy中计算总体方差
在numpy中,计算方法的函数是var (即variance的缩写),numpy中var方法默认计算的就是总体方差(计算时除以样本数 N),如需需要计算样本方差(计算时除以 N - 1),应设置参数 ddof = 1, 以下是在Numpy中计算总体方差的示例:
import numpy as np
a = np.arange(5)
print(f"数据集 = {a}")
print(f"总体方差 = {np.var(a)}")
输出如下:
数据集 = [0 1 2 3 4]
总体方差 = 2.0
2.1.2 在pandas中计算总体方差
在Pandas的DataFrame中,同样有用于计算行和列方差的函数,不过,与numpy不同的是,在pandas中默认计算的是样本方差(计算时除以 N - 1),如需需要计算总体方差(计算时除以样本数 N),应设置参数 ddof = 0。也就是说:在计算方差这件事上,numpy和pandas的默认行为是相反的,numpy默认计算总体方差,pandas默认计算样本方差。以下是在pandas中分别计算行和列的样本方差的示例:
import pandas as pd
df = pd.DataFrame(np.arange(5 * 5).reshape(5, 5))
print(f"数据集: \n{df}")
print(f"(行的)总体方差: \n{df.var(ddof=0,axis=1)}")
print(f"(列的)总体方差: \n{df.var(ddof=0)}")
输出如下:
数据集: 0 1 2 3 4
0 0 1 2 3 4
1 5 6 7 8 9
2 10 11 12 13 14
3 15 16 17 18 19
4 20 21 22 23 24
(行的)总体方差:
0 2.0
1 2.0
2 2.0
3 2.0
4 2.0
dtype: float64
(列的)总体方差:
0 50.0
1 50.0
2 50.0
3 50.0
4 50.0
dtype: float64
2.2 样本方差
但是在实际情况中,总体均值可能无法得到(样本过多或无法穷举),此时往往会通过抽样来获得一个近似值,这个值叫样本方差。
样本方差:

至于样本方差中的分母为什么是n-1,可以这样理解:因为样本方差是用来估计总体中个体之间的变化大小,只拿到一个个体,当然完全看不出变化大小。反之,如果公式的分母不是n-1而是n,计算出的方差就是0——这是不合理的,因为不能只看到一个个体就断定总体的个体之间变化大小为0。
2.2.1 在numpy中计算样本方差
如2.1.1节所述,numpy中默认计算的总体方差,如需计算样本方差,需在var函数中设置ddof = 1。以下是在Numpy中计算样本方差的示例:
import numpy as np
a = np.arange(5)
print(f"数据集 = {a}")
print(f"样本方差 = {np.var(a, ddof=1)}")
输出如下:
数据集 = [0 1 2 3 4]
样本方差 = 2.5
2.2.2 在pandas中计算样本方差
如2.1.2节所述,pandas中默认计算的就是样本方差,所以不需要设置ddof。以下是在Pandas中计算样本方差的示例:
import pandas as pd
df = pd.DataFrame(np.arange(5 * 5).reshape(5, 5))
print(f"数据集: \n{df}")
print(f"(行的)样本方差: \n{df.var(axis=1)}")
print(f"(列的)样本方差: \n{df.var()}")
输出如下:
数据集: 0 1 2 3 4
0 0 1 2 3 4
1 5 6 7 8 9
2 10 11 12 13 14
3 15 16 17 18 19
4 20 21 22 23 24
(行的)样本方差:
0 2.5
1 2.5
2 2.5
3 2.5
4 2.5
dtype: float64
(列的)样本方差:
0 62.5
1 62.5
2 62.5
3 62.5
4 62.5
dtype: float64
3. 标准差 / 均方差 (Standard Deviation)
标准差又常称均方差,是方差的算术平方根。均方差反映的也是一组数据的离散程度。其实方差与标准差反映的都是数据集的离散程度,只是由于方差出现了平方项,导致量纲与原始数据量纲不一致,无法直观反映出偏离程度,所以才有了标准差。
正因为均方差是方差的平方根,所以对应于总体方差和样本方差,就总体均方差(总体标准差)和样本均方差(样本标准差),它们的计算公式分别是:
3.1 总体标准差

3.1.1 在numpy中计算总体标准差
在numpy中,计算标准差的函数是std (即standard的缩写),与var方法一样,numpy中std方法默认计算的就是总体标准差(计算时除以样本数 N),如需需要计算样本标准差(计算时除以 N - 1),应设置参数 ddof = 1, 以下是在Numpy中计算总体标准差的示例:
import numpy as np
a = np.arange(5)
print(f"数据集 = {a}")
print(f"总体标准差 = {np.std(a)}")
输出如下:
数据集 = [0 1 2 3 4]
总体标准差 = 1.4142135623730951
3.1.2 在pandas中计算总体标准差
在Pandas的DataFrame中,同样有用于计算行和列标准差的函数,不过,与numpy不同的是,在pandas中默认计算的是样本标准差(计算时除以 N - 1),如需需要计算总体标准差(计算时除以样本数 N),应设置参数 ddof = 0。也就是说:在计算标准差这件事上,numpy和pandas的默认行为是相反的,numpy默认计算总体标准差,pandas默认计算样本标准差。以下是在pandas中分别计算行和列的总体标准差的示例:
import pandas as pd
df = pd.DataFrame(np.arange(5 * 5).reshape(5, 5))
print(f"数据集: \n{df}")
print(f"(行的)总体标准差: \n{df.std(ddof=0, axis=1)}")
print(f"(列的)总体标准差: \n{df.std(ddof=0,)}")
输出如下:
数据集: 0 1 2 3 4
0 0 1 2 3 4
1 5 6 7 8 9
2 10 11 12 13 14
3 15 16 17 18 19
4 20 21 22 23 24
(行的)总体标准差:
0 1.414214
1 1.414214
2 1.414214
3 1.414214
4 1.414214
(列的)总体标准差:
0 7.071068
1 7.071068
2 7.071068
3 7.071068
4 7.071068
dtype: float64
3.2 样本标准差

3.2.1 在numpy中计算样本标准差
在numpy中,计算标准差的函数是std (即standard的缩写),与var方法一样,numpy中std方法默认计算的就是总体标准差(计算时除以样本数 N),如需需要计算样本标准差(计算时除以 N - 1),应设置参数 ddof = 1, 以下是在Numpy中计算样本标准差的示例:
import numpy as np
a = np.arange(5)
print(f"数据集 = {a}")
print(f"样本标准差 = {np.std(a, ddof=1)}")
输出如下:
数据集 = [0 1 2 3 4]
样本标准差 = 1.5811388300841898
3.2.2 在pandas中计算样本标准差
如3.1.2节所述,pandas中默认计算的就是样本标准差,所以不需要设置ddof。以下是在Pandas中计算样本标准差的示例:
import pandas as pd
df = pd.DataFrame(np.arange(5 * 5).reshape(5, 5))
print(f"数据集: \n{df}")
print(f"(列的)样本标准差: \n{df.std()}")
输出如下:
数据集: 0 1 2 3 4
0 0 1 2 3 4
1 5 6 7 8 9
2 10 11 12 13 14
3 15 16 17 18 19
4 20 21 22 23 24
(行的)样本标准差:
0 1.581139
1 1.581139
2 1.581139
3 1.581139
4 1.581139
dtype: float64
(列的)样本标准差:
0 7.905694
1 7.905694
2 7.905694
3 7.905694
4 7.905694
dtype: float64
4. 均方误差(mean-square error, MSE)
均方误差MSE通过计算预测值和实际值之间距离(即误差)的平方来衡量模型优劣。即预测值和真实值越接近,两者的均方差就越小。MSE的值越小,说明预测模型描述实验数据具有更好的精确度。均方误差损失又称为二次损失、L2损失,常用于回归预测任务中。如下是均方误差的计算方法:

基于上述表述,均方误差也会这样表述:

其中observed(t)就是针对数据t的实际输出值(观测到的值),predicted(t)就是对应的预测值。
其实从均方误差MSE的计算公式可以看出,它和方差是高度一致的,只是参与计算的变量(项)不同,所以度量的角度也就不同,方差是用来衡量一组数自身的离散程度,而均方误差是用来衡量观测值(真值)与预测值之间的偏差。
最后,还有一小细节需要注意一下:均方误差的计算除以的是N不是N-1,因为预测值是有限的,和测试用的实际值也是一一对应的,所以,再准确一点说,均方误差的计算与总体方差计算公式相同,除的是N不是N-1。
5. 标准误差 / 均方根误差(root mean squared error,RMSE)
均方根误差也称之为标准误差,是均方误差的算术平方根。引入均方根误差与引入标准差(均方查)的原因是完全一致的,即均方误差的量纲与数据量纲不同,不能直观反映离散程度,故在均方误差上开平方根,得到均方根误差:

同样的,均方根误差RMSE和标准差的计算公式也是高度近似的:标准差是用来衡量一组数自身的离散程度,而均方根误差是用来衡量观测值(真值)与预测值之间的偏差。
6. 所有值的计算方法汇总
import numpy as np
a = np.arange(5)
print(f"数据集 = {a}")
print(f"总体方差 = {np.var(a)}")
print(f"样本方差 = {np.var(a, ddof=1)}")
print(f"总体标准差 = {np.std(a)}")
print(f"样本标准差 = {np.std(a, ddof=1)}")import pandas as pd
df = pd.DataFrame(np.arange(5 * 5).reshape(5, 5))
print(f"数据集: \n{df}")
print(f"(行的)总体方差: \n{df.var(ddof=0, axis=1)}")
print(f"(列的)总体方差: \n{df.var(ddof=0)}")
print(f"(行的)样本方差: \n{df.var(axis=1)}")
print(f"(列的)样本方差: \n{df.var()}")
print(f"(行的)总体标准差: \n{df.std(ddof=0, axis=1)}")
print(f"(列的)总体标准差: \n{df.std(ddof=0)}")
print(f"(行的)样本标准差: \n{df.std(axis=1)}")
print(f"(列的)样本标准差: \n{df.std()}")
输出如下:
数据集 = [0 1 2 3 4]
总体方差 = 2.0
样本方差 = 2.5
总体标准差 = 1.4142135623730951
样本标准差 = 1.5811388300841898
数据集: 0 1 2 3 4
0 0 1 2 3 4
1 5 6 7 8 9
2 10 11 12 13 14
3 15 16 17 18 19
4 20 21 22 23 24
(行的)总体方差:
0 2.0
1 2.0
2 2.0
3 2.0
4 2.0
dtype: float64
(列的)总体方差:
0 50.0
1 50.0
2 50.0
3 50.0
4 50.0
dtype: float64
(行的)样本方差:
0 2.5
1 2.5
2 2.5
3 2.5
4 2.5
dtype: float64
(列的)样本方差:
0 62.5
1 62.5
2 62.5
3 62.5
4 62.5
dtype: float64
(行的)总体标准差:
0 1.414214
1 1.414214
2 1.414214
3 1.414214
4 1.414214
dtype: float64
(列的)总体标准差:
0 7.071068
1 7.071068
2 7.071068
3 7.071068
4 7.071068
dtype: float64
(行的)样本标准差:
0 1.581139
1 1.581139
2 1.581139
3 1.581139
4 1.581139
dtype: float64
(列的)样本标准差:
0 7.905694
1 7.905694
2 7.905694
3 7.905694
4 7.905694
dtype: float64参考文章:
方差、协方差、标准差、均方差、均方根值、均方误差、均方根误差对比分析
均方差损失(Mean Square Error,MSE)