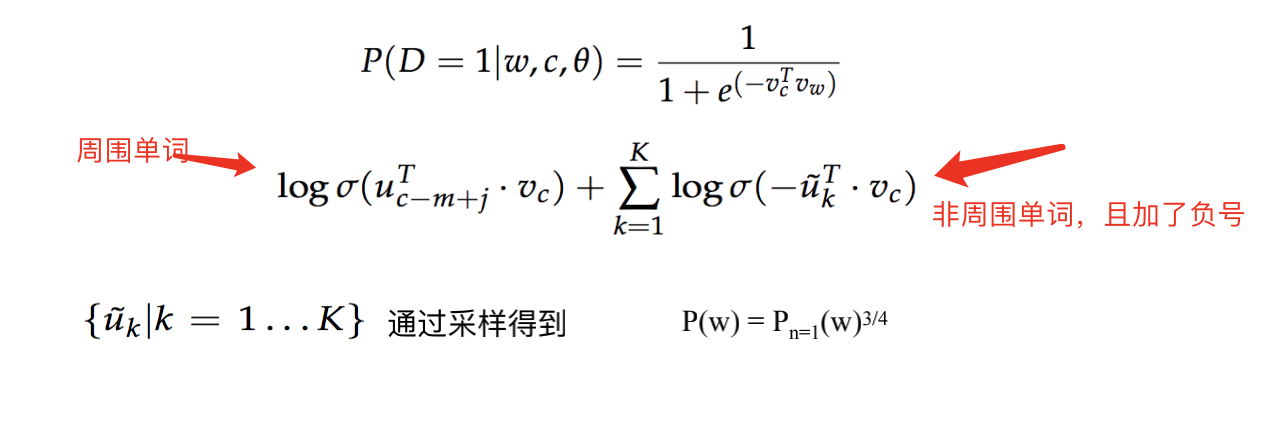统计语言模型

语言模型基本概念

弗莱德里克·贾里尼克提出用数学的方法描述语言规律（语言模型）

语言模型基本思想：

用句子 $S=w_{1},w_{2},...,w_{n}$ 的概率P(S)刻画句子的合理性（统计自然语言处理的基础模型）

$p(S)=p(w_{1})p(w_{2}|w_{1})...p(w_{n}|w_{1},...,w_{n-1})=\prod_{i=1}^{n}p(w_{i}|w_{1}...w_{i-1})$

当 i=1 时， $p (w 1∣ w 0) = p (w 1)$

语言模型：

输入：句子S
输出：句子概率p(S)
参数： $p(w_{i}|w_{1}...w_{i-1})$
函数关系： $p(S)=\prod_{i=1}^{n}p(w_{i}|w_{1}...w_{i-1})$

注：

$w_{i}$ 可以是字、词、短语或词类等，统称为基元

存在问题：模型参数过多
解决办法：减少历史基元个数，马尔可夫方法：假设任意一个词出现的概率只与它前面的一个词有关

$p(S)=p(w_{1})p(w_{2}|w_{1})...p(w_{i}|w_{i-1})$ (二元模型)

语言模型参数估计

任务：获得语言模型中所有词的条件概率（语言模型参数）

参数估计：
1、训练语料
2、参数学习方法：采用极大似然估计方法

参数的数据平滑

基本思想：调整最大似然估计的概率值，使零概率增值，非零概率下调，消除零概率，改进模型的整体正确率。

方法：
1、加1法
2、减值法/折扣法
3、删除减值法：低阶代替高阶
…

基本目标：测试样本的语言模型困惑度越小越好

基本约束： $\sum_{w_{i}}p(w_{i}|w_{1},w_{2},...,w_{i-1})=1$

语言模型性能评价

1、实用方法：
查看模型在实际应用中的表现来评价
2、理论方法
困惑度，低困惑度的语言模型较好

困惑度定义：

语言模型应用

决定哪一个词序列的可能性更大
预测下一个词
…

语言模型的变种

前向-后向语言模型

跟前一个词有关或者跟后一个词有关

K-Skipping

一个词出现的概率只与它前（后）面的距离为K的n-1个词相关。核心思想是刻画远距离约束关系

Class-based

基于词类建立语言模型，缓解数据稀疏问题

指数语言模型
Topic-based
Cache-based

神经语言模型

神经语言模型概述

用神经网络学习参数

使用DNN学习模型参数：NNLM模型
使用RNN学习模型参数：RNNLM模型

DNN语言模型NNLM

目标：使用DNN学习语言模型p(S)和模型参数
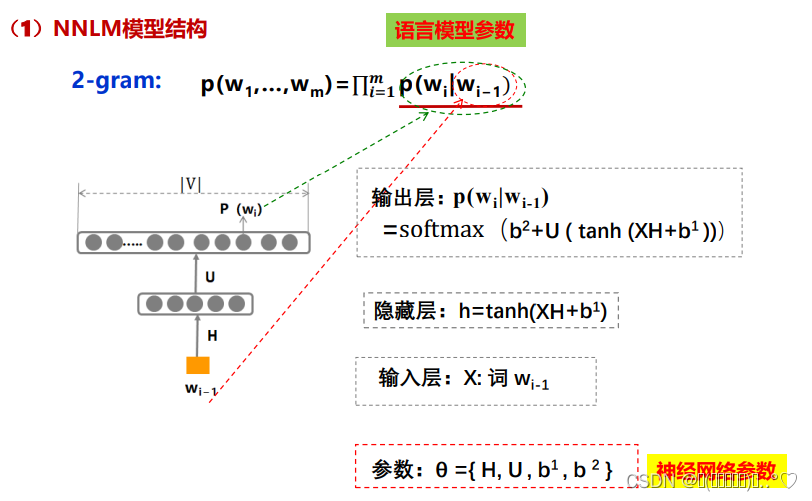
NNLM/2-gram：

2元文法模型： $p(w_{1},...,w_{m})=\prod_{i=1}^{m}p(w_{i}|w_{i-1})$
参数： $p(w_{i}|w_{i-1})$
任务：用DNN学习参数
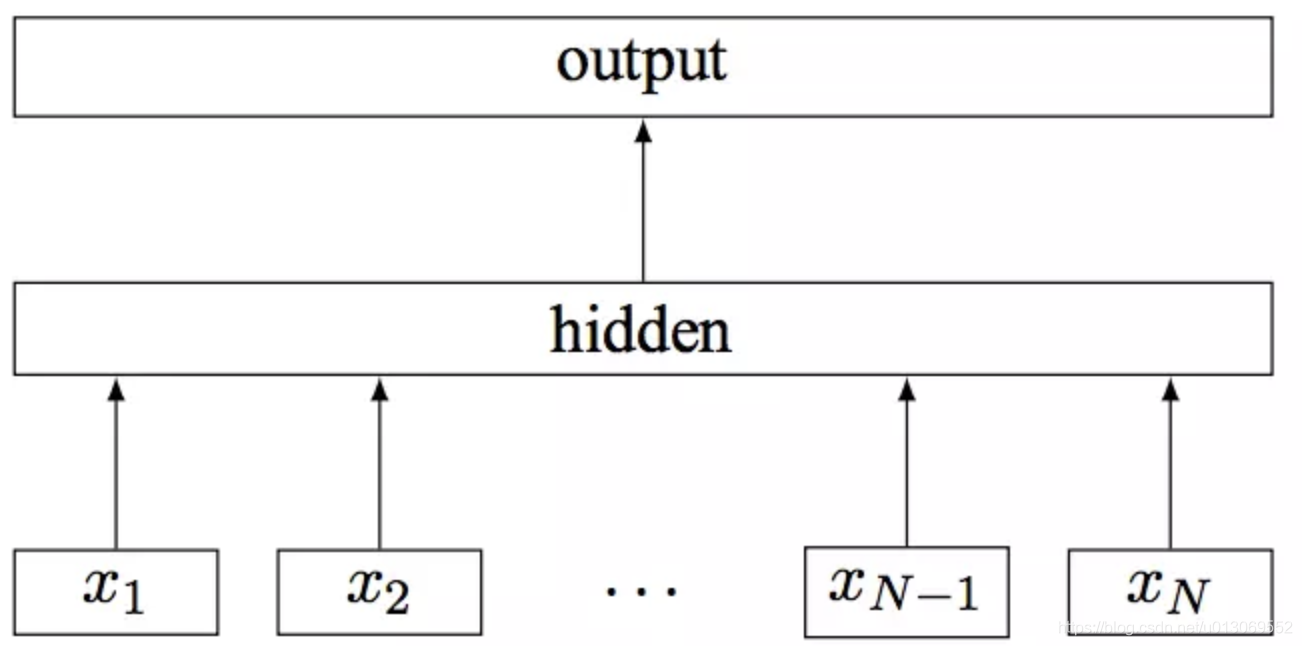
模型设计：

神经网络：DNN
输入： $w_{i-1}$
输出： $p(w_{i})$

语料：（“无监督”）
文本：S=w1,w2,…,wn,…
实例： $X:w_{i-1},\hat{Y}:w_{i}$

目标函数：

采用log损失函数： $L (Y, P (Y ∣ X)) = - l o g P (Y ∣ X)$
最大化： $\sum_{w_{i-1},i\epsilon D}logP(w_{i}|w_{i-1})$

参数训练：随机梯度下降法优化训练目标

RNN语言模型RNNLM

目标：用神经网络RNN学习语言模型 $p(S)=\prod_{i=1}^{n}p(w_{i}|w_{1}...w_{i-1})$
模型参数： $p(w_{i}|w_{i-(n-1)}...w_{i-1})$

随着模型逐个读入语料中的词w1,w2…，隐藏层不断地更新h(1),h(2),…，通过这种迭代推进方式，每个隐藏层实际上包含了此前所有上文的信息，相比NNLM只能采用上文n元短语作为近似，RNNLM包含了更丰富的上文信息，有潜力达到更好的效果

RNN语言模型变形

正向语言模型
反向语言模型
双向语言模型
单向多层RNN语言模型
双向多层RNN语言模型

词向量（浅层）

词向量概述

词的表示

符号表示

离散表示
1、one-hot表示

优势：稀疏方式存储非常的简洁
不足：词汇鸿沟，维数灾难

2、词袋模型

每个数表示该词在文档中出现的次数（one-hot的加和）

3、TF_IDF

每个数代表该词在整个文档中的占比

词的分布式表示

核心思想：用一个词附近的其他词来表示该词
分布式假设：在相同上下文中出现的词倾向于具有相同的含义
分布式语义学：根据词语在大型文本语料中的分布特性量化词语及词语语义相似性

经典分布表示模型