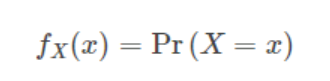模块是程序加载时被动态装载的,模块在装载后其存在于内存中同样存在一个内存基址,当我们需要操作这个模块时,通常第一步就是要得到该模块的内存基址,模块分为用户模块和内核模块,这里的用户模块指的是应用层进程运行后加载的模块,内核模块指的是内核中特定模块地址,本篇文章将实现一个获取驱动ntoskrnl.exe的基地址以及长度,此功能是驱动开发中尤其是安全软件开发中必不可少的一个功能。
关于该程序的解释,官方的解析是这样的ntoskrnl.exe是Windows操作系统的一个重要内核程序,里面存储了大量的二进制内核代码,用于调度系统时使用,也是操作系统启动后第一个被加载的程序,通常该进程在任务管理器中显示为System。
使用ARK工具也可看出其代表的是第一个驱动模块。
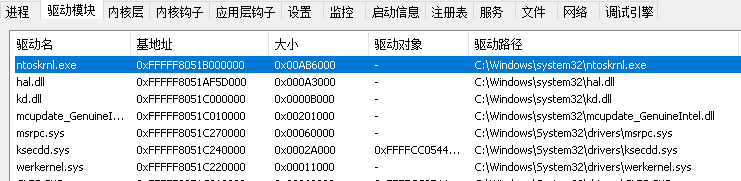
那么如何使用代码得到如上图中所展示的基地址以及大小呢,实现此功能我们需要调用ZwQuerySystemInformation这个API函数,这与上一篇文章《驱动开发:判断自身是否加载成功》所使用的NtQuerySystemInformation只是开头部分不同,但其本质上是不同的,如下是一些参考资料;
-
从内核模式调用
Nt和Zw系列API,其最终都会连接到nooskrnl.lib导出库:- Nt系列API将直接调用对应的函数代码,而Zw系列API则通过调用
KiSystemService最终跳转到对应的函数代码。 - 重要的是两种不同的调用对内核中
previous mode的改变,如果是从用户模式调用Native API则previous mode是用户态,如果从内核模式调用Native API则previous mode是内核态。 - 如果
previous为用户态时Native API将对传递的参数进行严格的检查,而为内核态时则不会检查。
- Nt系列API将直接调用对应的函数代码,而Zw系列API则通过调用
调用Nt API时不会改变previous mode的状态,调用Zw API时会将previous mode改为内核态,因此在进行Kernel Mode Driver开发时可以使用Zw系列API可以避免额外的参数列表检查,提高效率。Zw*会设置KernelMode已避免检查,Nt*不会自动设置,如果是KernelMode当然没问题,如果就UserMode就挂了。
回到代码上来,下方代码就是获取ntoskrnl.exe基地址以及长度的具体实现,核心代码就是调用ZwQuerySystemInformation得到SystemModuleInformation,里面的对比部分是在比较当前获取的地址是否超出了ntoskrnl的最大和最小范围。
#include <ntifs.h>static PVOID g_KernelBase = 0;
static ULONG g_KernelSize = 0;#pragma pack(4)
typedef struct _PEB32
{UCHAR InheritedAddressSpace;UCHAR ReadImageFileExecOptions;UCHAR BeingDebugged;UCHAR BitField;ULONG Mutant;ULONG ImageBaseAddress;ULONG Ldr;ULONG ProcessParameters;ULONG SubSystemData;ULONG ProcessHeap;ULONG FastPebLock;ULONG AtlThunkSListPtr;ULONG IFEOKey;ULONG CrossProcessFlags;ULONG UserSharedInfoPtr;ULONG SystemReserved;ULONG AtlThunkSListPtr32;ULONG ApiSetMap;
} PEB32, *PPEB32;typedef struct _PEB_LDR_DATA32
{ULONG Length;UCHAR Initialized;ULONG SsHandle;LIST_ENTRY32 InLoadOrderModuleList;LIST_ENTRY32 InMemoryOrderModuleList;LIST_ENTRY32 InInitializationOrderModuleList;
} PEB_LDR_DATA32, *PPEB_LDR_DATA32;typedef struct _LDR_DATA_TABLE_ENTRY32
{LIST_ENTRY32 InLoadOrderLinks;LIST_ENTRY32 InMemoryOrderLinks;LIST_ENTRY32 InInitializationOrderLinks;ULONG DllBase;ULONG EntryPoint;ULONG SizeOfImage;UNICODE_STRING32 FullDllName;UNICODE_STRING32 BaseDllName;ULONG Flags;USHORT LoadCount;USHORT TlsIndex;LIST_ENTRY32 HashLinks;ULONG TimeDateStamp;
} LDR_DATA_TABLE_ENTRY32, *PLDR_DATA_TABLE_ENTRY32;
#pragma pack()typedef struct _RTL_PROCESS_MODULE_INFORMATION
{HANDLE Section;PVOID MappedBase;PVOID ImageBase;ULONG ImageSize;ULONG Flags;USHORT LoadOrderIndex;USHORT InitOrderIndex;USHORT LoadCount;USHORT OffsetToFileName;UCHAR FullPathName[256];
} RTL_PROCESS_MODULE_INFORMATION, *PRTL_PROCESS_MODULE_INFORMATION;typedef struct _RTL_PROCESS_MODULES
{ULONG NumberOfModules;RTL_PROCESS_MODULE_INFORMATION Modules[1];
} RTL_PROCESS_MODULES, *PRTL_PROCESS_MODULES;typedef enum _SYSTEM_INFORMATION_CLASS
{SystemModuleInformation = 0xb,
} SYSTEM_INFORMATION_CLASS;// 取出KernelBase基地址
// By: lyshark.com
PVOID UtilKernelBase(OUT PULONG pSize)
{NTSTATUS status = STATUS_SUCCESS;ULONG bytes = 0;PRTL_PROCESS_MODULES pMods = 0;PVOID checkPtr = 0;UNICODE_STRING routineName;if (g_KernelBase != 0){if (pSize)*pSize = g_KernelSize;return g_KernelBase;}RtlInitUnicodeString(&routineName, L"NtOpenFile");checkPtr = MmGetSystemRoutineAddress(&routineName);if (checkPtr == 0)return 0;__try{status = ZwQuerySystemInformation(SystemModuleInformation, 0, bytes, &bytes);if (bytes == 0){DbgPrint("Invalid SystemModuleInformation size\n");return 0;}pMods = (PRTL_PROCESS_MODULES)ExAllocatePoolWithTag(NonPagedPoolNx, bytes, "lyshark");RtlZeroMemory(pMods, bytes);status = ZwQuerySystemInformation(SystemModuleInformation, pMods, bytes, &bytes);if (NT_SUCCESS(status)){PRTL_PROCESS_MODULE_INFORMATION pMod = pMods->Modules;for (ULONG i = 0; i < pMods->NumberOfModules; i++){if (checkPtr >= pMod[i].ImageBase &&checkPtr < (PVOID)((PUCHAR)pMod[i].ImageBase + pMod[i].ImageSize)){g_KernelBase = pMod[i].ImageBase;g_KernelSize = pMod[i].ImageSize;if (pSize)*pSize = g_KernelSize;break;}}}}__except (EXCEPTION_EXECUTE_HANDLER){return 0;}if (pMods)ExFreePoolWithTag(pMods, "lyshark");return g_KernelBase;
}VOID UnDriver(PDRIVER_OBJECT driver)
{DbgPrint(("Uninstall Driver Is OK \n"));
}NTSTATUS DriverEntry(IN PDRIVER_OBJECT Driver, PUNICODE_STRING RegistryPath)
{DbgPrint(("hello lyshark \n"));PULONG ulong = 0;UtilKernelBase(ulong);DbgPrint("ntoskrnl.exe 模块基址: 0x%p \n", g_KernelBase);DbgPrint("模块大小: 0x%p \n", g_KernelSize);Driver->DriverUnload = UnDriver;return STATUS_SUCCESS;
}
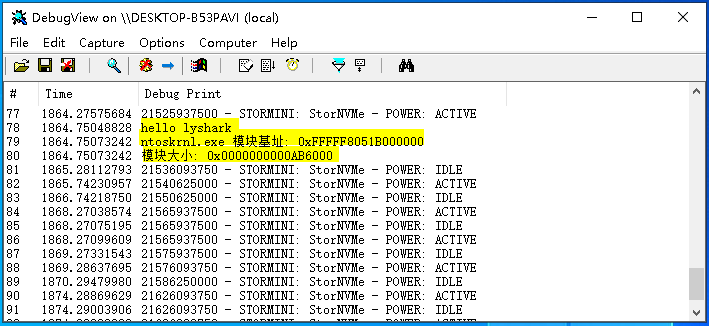
我们编译并运行上方代码,效果如下:
参考文献:
https://blog.csdn.net/u012410612/article/details/17096597