目录
贪心算法
例题
活动安排问题
背包问题
删数问题
多处最优服务次序
贪心算法
在求最优解问题的过程中,依据某种贪心标准,从问题的初始状态出发,直接去求每一步的最优解,通过若干次的贪心选择,最终得出整个问题的最优解,这种求解方法就是贪心算法。
贪心算法不是从整体上考虑问题,而是在每一步选择中都采取在当前状态下最优的选择,即希望通过问题的局部最优解求出整个问题的最优解。
这种策略是一种很简洁的方法,对许多问题它能产生整体最优解,但不能保证总是有效,因为它不是对所有问题都能得到整体最优解。
如果一个问题可以同时用几种方法解决,贪心算法应该是最好的选择之一。
利用贪心策略解题,需要解决两个问题:
- (1)该题是否适合于用贪心策略求解;
- (2)如何选择贪心标准,以得到问题的最优/较优解。
例题
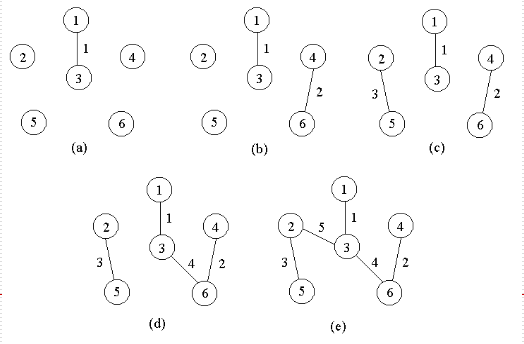
活动安排问题
1.描述
设有n个活动的集合E={1,2,…,n},每个活动都要使用同一资源,如演讲会场等,而在同一时间段内只有一个活动能使用这一资源。
每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si<fi。如果选择了活动i,则在[si ,fi )内占用资源。
若区间[si ,fi )与区间[sj,fj )不相交,则称活动i与活动j是相容的。
活动安排问题就是在所给的活动集合中选出最大的相容活动子集合。
此时追求的最优是在最短的时间内安排最多的活动
2.思路
按照起止时间排序:有可能遇到初始时间很早,但结束时间很晚的活动。不合适
按照终止时间排序:优先选择较早终止且不与前面活动相交的活动
3.代码
#include <iostream>
#include <stdio.h>
#include <algorithm>
using namespace std;
struct action{int s;//起始时间int f;//结束时间int index;//活动的变化
};bool cmp(const action &a,const action &b){if(a.f<=b.f)return true;return false;
}void GreedySelector(int n,action a[],bool b[]){b[1]=true;//选中排序后的第一个活动int preEnd=1;//记录最近一次加入集合b的活动for(int i=2;i<=n;i++)if(a[i].s>=a[preEnd].f){b[i]=true;preEnd=i;}}
int main()
{action a[1001];int n;scanf("%d",&n);bool b[n+1];for(int i=1;i<=n;i++){scanf("%d%d%d",&a[i].s,&a[i].f,&a[i].index);b[i]=false;}sort(a,a+n+1,cmp);GreedySelector(n,a,b);for(int i=1;i<=n;i++)if(b[i])printf("%d\n",a[i].index);return 0;
}
背包问题
1.描述
给定一个载重量为M的背包,考虑n个物品,其中第i个物品的重量 ,价值wi (1≤i≤n),要求把物品装满背包,且使背包内的物品价值最大。
- 如果物品不可以分割,称为0—1背包问题(动态规划),可以参考我另一篇博客
- 如果物品可以分割,则称为背包问题(贪心算法)。
2.思路
有3种方法来选取物品:
- (1)当作0—1背包问题,用动态规划算法,获得最优值220;
- (2)当作0—1背包问题,用贪心算法,按性价比从高到底顺序选取物品,获得最优值160。由于物品不可分割,剩下的空间白白浪费,不是最优。
- (3)当作背包问题,用贪心算法,按性价比从高到底的顺序选取物品,获得最优值240。由于物品可以分割,剩下的空间装入物品3的一部分,而获得了更好的性能。




3.代码
#include <iostream>
#include <stdio.h>
#include <algorithm>
using namespace std;
struct bag{int w;//物品的重量int v;//物品的价值double c;//性价比double x;//此物品装入背包的量int index;
};bool cmp(bag a,bag b){if(a.c>=b.c)return true;return false;//return a.c>=b.c;
}double pack(int n,bag a[],double c){double cleft=c;//背包的剩余容量int i=0;double b=0;//装入物品的总价值//背包可以直接装入一个物品iwhile(i<n&&a[i].w<cleft){cleft-=a[i].w;b+=a[i].v;a[a[i].index].x=1.0;i++;}//把物品分割后装满背包if(i<n){a[a[i].index].x=1.0*cleft/a[i].w;b+=a[a[i].index].x*a[i].v;}return b;
}int main()
{bag a[1001];int n,c;scanf("%d%d",&n,&c);for(int i=0;i<n;i++){scanf("%d%d%lf%d",&a[i].w,&a[i].v,&a[i].c,&a[i].index);a[i].x=0;}sort(a,a+n,cmp);printf("%f\n",pack(n,a,c));for(int i=0;i<n;i++)if(a[i].x!=0)printf("%d:%f\n",a[i].index,a[i].x);return 0;
}
删数问题
1.描述
给定n位正整数a,去掉其中任意k≤n个数字后,剩下的数字按原次序排列组成一个新的正整数。对于给定的n位正整数a和正整数k,设计一个算法找出剩下数字组成的新数最小的删数方案。
输入:第1行是1个正整数a,第2行是正整数k。
输出:对于给定的正整数a,编程计算删去k个数字后得到的最小数。
2.思路
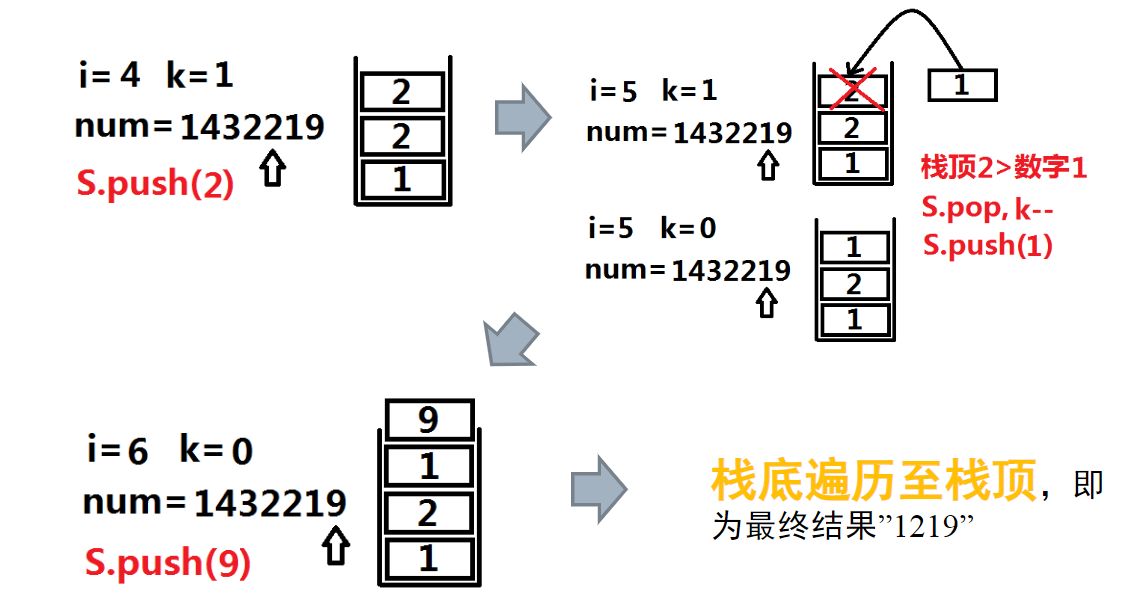
n位数a,n可能特别大,因此可以用字符串存放,a表示为x1x2… xn,要删去k位数,使得剩下的数字组成的整数最小。
将该问题记为T,最优解A=xi1 xi2…xim (i1<i2<..<im,m=n-k),在删去k个数后剩下的数字按原次序排成的新数,其最优值记为N。
采用最近下降点优先的贪心策略:即x1<x2<... <xi-1<xi,如果xi+1<xi(下降点),则删去xi,即得到一个新的数且这个数为n-1位中最小的数N,可表示为x1x2…xi-1 xi+1...xn。
显然删去1位数后,原问题T变成了对n- 1位数删去k- 1个数的新问题T'
新问题和原问题性质相同,只是问题规模由n减小为n-1,删去的数字个数由k减少为k-1。
基于此种删除策略,对新问题T’,选择最近下降点的数继续进行删除,直至删去k个数为止。
3.代码
#include <iostream>
#include <cstring>
using namespace std;int main()
{string a;int k,i;cin>>a>>k;if(k>=a.size())a.erase();elsewhile(k>0){i=0;while(a[i]<=a[i+1])i++;if(i<a.size()-1){//cout<<"a:"<<a<<endl;a.erase(i,1);//取出a[i]k--;//针对12345这种情况,删5-4-3……}else if(i == a.size()-1){a.erase(i,1);k--;}//cout<<"k:"<<k<<endl;}while(a.size()>1&&a[0]=='0')a.erase(0,1);cout<<a<<endl;return 0;
}
多处最优服务次序
1.描述
设有n个顾客同时等待一项服务,顾客i需要的服务时间为ti,1≤i≤n,共有s处可以提供此项服务。应如何安排n个顾客的服务次序才能使平均等待时间达到最小?平均等待时间是n个顾客等待服务时间的总和除以n。
给定的n个顾客需要的服务时间和s的值,编程计算最优服务次序。
输入:第一行有2个正整数n和s,表示有n个顾客且有s处可以提供顾客需要的服务。接下来的一行中,有n个正整数,表示n个顾客需要的服务时间。
输出:最小平均等待时间,输出保留3位小数。
2.思路
假设原问题为T,并已经知道某个最优服务序列,即最优解为A={t1,t2....tn,其中ti为第i个用户需要的服务时间,则每个用户等待时间T为:
T1=t1;
T2=t1 + t2;
Tn=t1 + t2+...+tn
那么总的等待时间,即最优值N为:
N=nt1 + (n - 1)t2+…+2tn-1+tn
平均等待时间是n个顾客等待时间的总和除以n,故本题实际上就是求使顾客等待时间的总和最小的服务次序。
贪心策略:对服务时间最短的顾客先服务。
首先对需要服务时间最短的顾客进行服务,即做完第一次选择后,原问题T变成了需对n-1个顾客服务的新问题T’。 新问题和原问题相同,只是问题规模由n减小为n-1。
3.代码
#include <iostream>
#include <algorithm>
#include <stdio.h>
#include <string.h>
using namespace std;//顾客等待的队列为client,提供服务的窗口s个
double greedy(int client[],int s,int n){//服务窗口的顾客等待时间int service[s+1];//服务窗口顾客等待时间的总和int sum[s+1];//按顾客的服务时间升序排序sort(client,client+n);//初始化memset(service,0,sizeof(service));memset(sum,0,sizeof(sum));//贪心算法int i=0;//顾客的指针int j=0;//窗口的指针while(i<n){service[j]+=client[i];sum[j]+=service[j];i++;j++;if(j==s)j=0;}double t=0;for(i=0;i<s;i++)t+=sum[i];t/=n;return t;
}int main()
{int client[1000];int s,n;scanf("%d%d",&n,&s);//顾客数,窗口数for(int i=0;i<n;i++)scanf("%d",&client[i]);printf("%f",greedy(client,s,n));return 0;
}