目录
问题
问题实例
问题分析
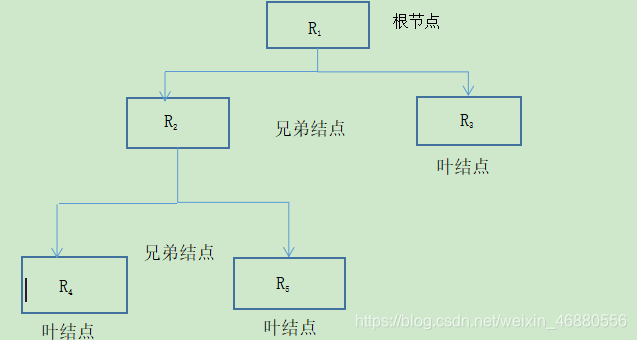
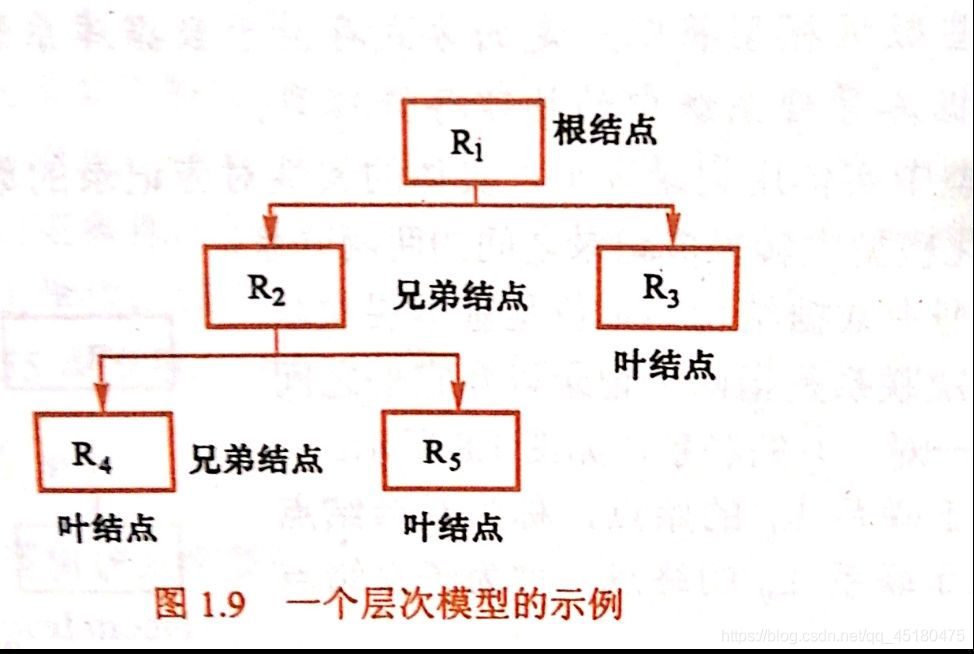
建立层次分析法模型
分析权重的方法
编辑
填表指标的权重编辑
一致性检验
一致性检验的引入
一致性检验的步骤
计算判断矩阵
归一化处理
算术平均法求权重
几何平均法求权重
特征值法求权重(常用)
汇总结果,得出结论
得出权重矩阵
计算得分
得出结论
代码部分
Matlab入门知识
本文例题代码计算部分
撰写论文部分
他人的例子(选自2016创新奖B题)
一些技巧
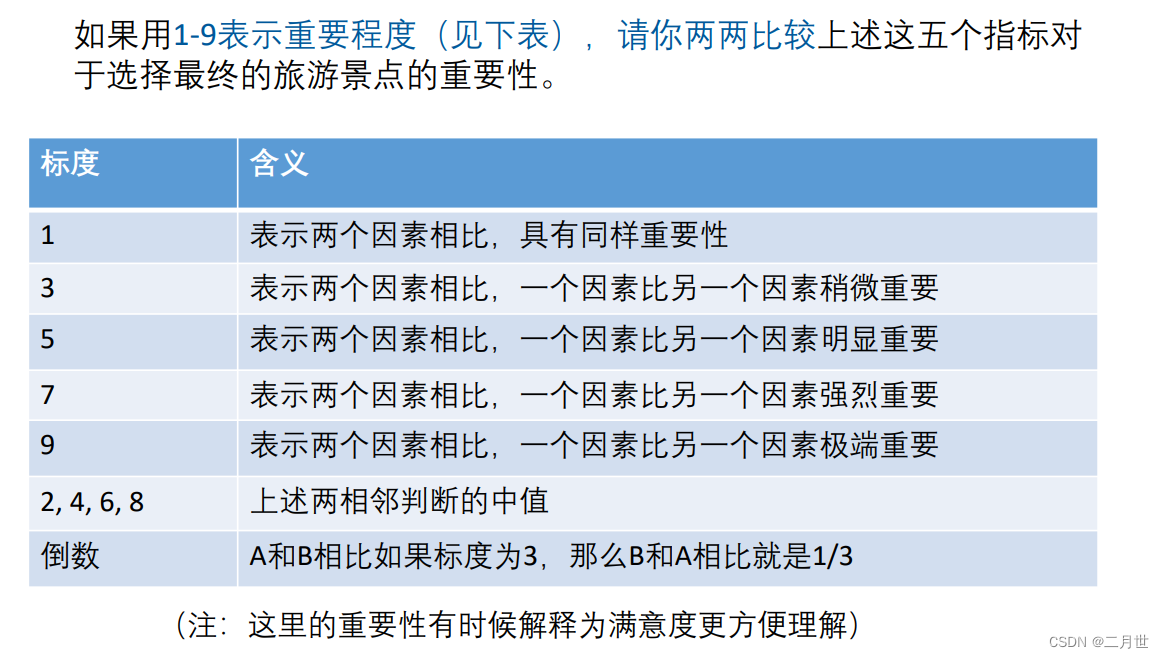
问题
问题实例

问题分析

推荐搜索网站:虫部落 https://www.chongbuluo.com/
确定指标为:
景点景色,旅游花费,居住环境,饮食情况,交通便利程度
建立层次分析法模型
分析权重的方法

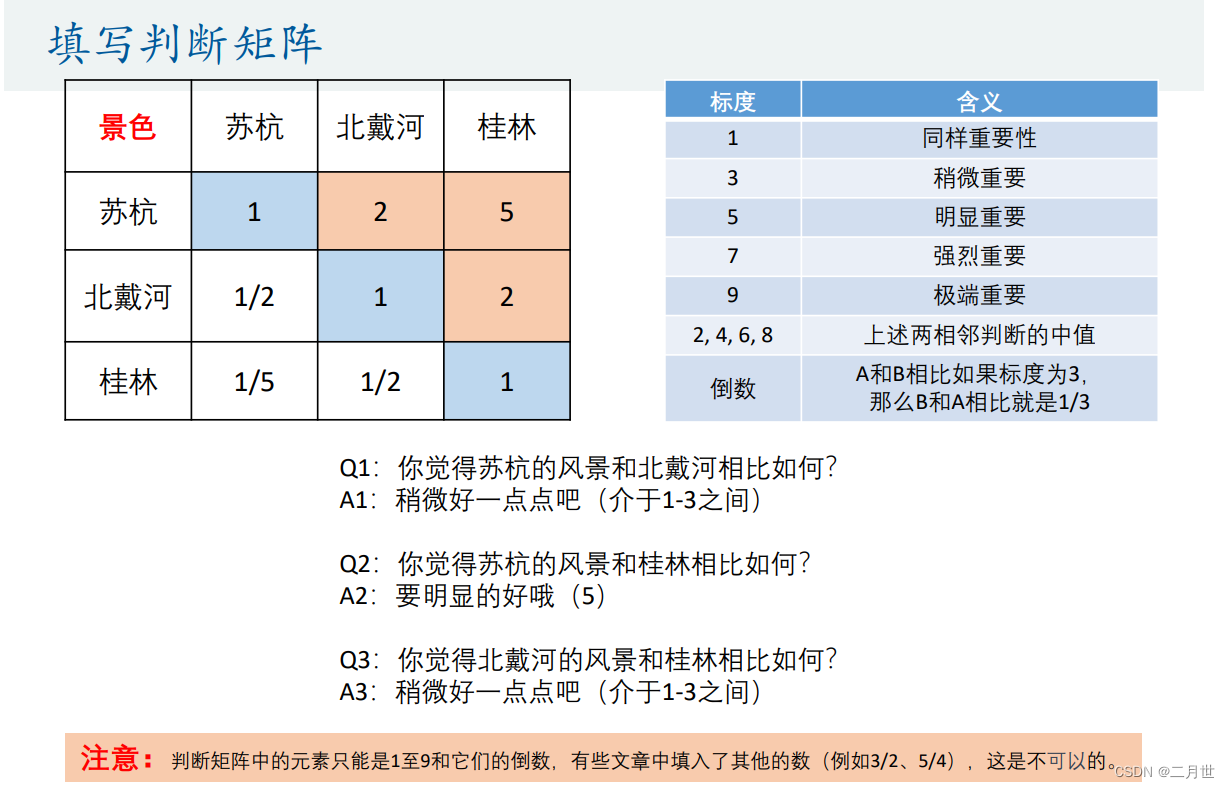
填表指标的权重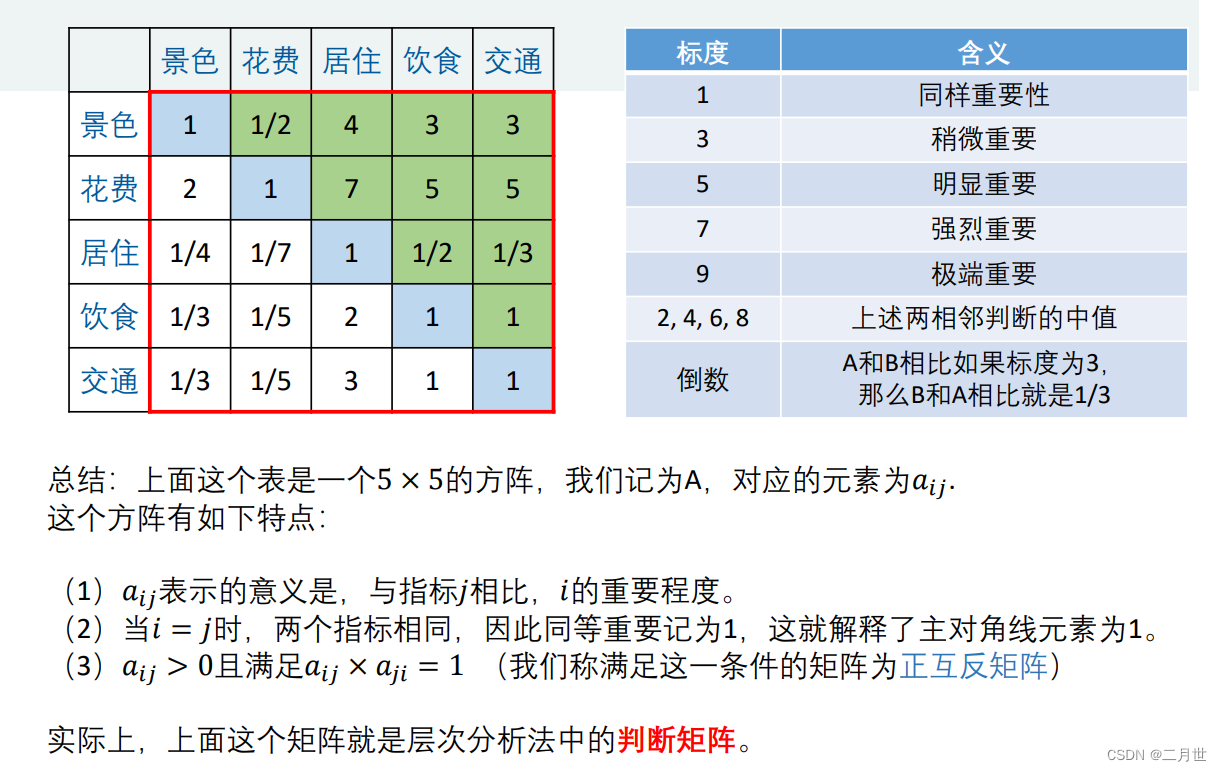
同理得到方案的权重的判断矩阵(例子)
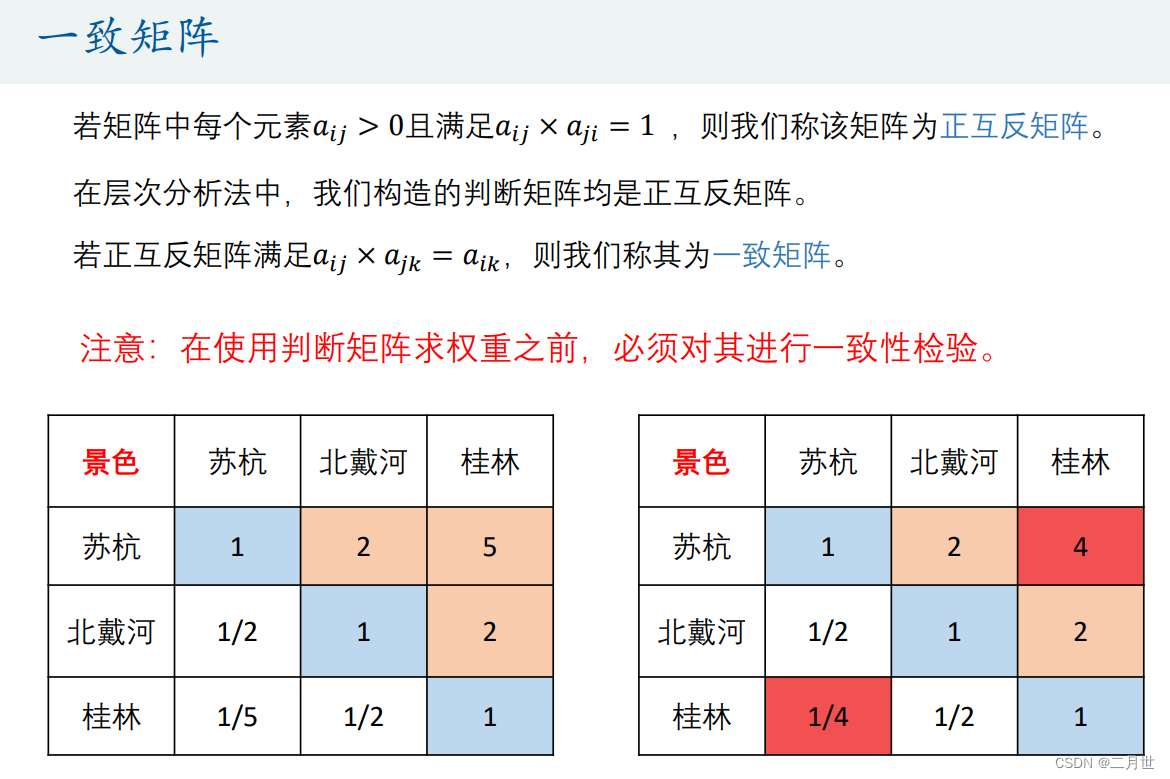
一致性检验
一致性检验的引入

 矩阵的秩为1时,其一特征值为对角线之和,其余特征值为0
矩阵的秩为1时,其一特征值为对角线之和,其余特征值为0
具体证法(来源网络)(推荐手机)https://vt.quark.cn/blm/quark-doc-ssr-293/preview?PageNum=1&bi=35823&ch=kk%40store&de=AANmbWuCsNJjJuHiN4nNjNNrIbUqF3IGiixbrKnuC%252FFU6A%253D%253D&dn=49492697401-9bf53019&ds=AAO3jqGiP6RzKox%2FKmKSp6aQa2lVksVIPKXkS2dt1FDQNg%3D%3D&ei=bTkwBAFH4DT%2Fh3SoyOphaRkAazmaVXkSCg%3D%3D&fp_from=sc&fr=android&gi=bTkwBDddBvWRpgZgFtlHKaFunbMg9eJnF8DTnjx5msb056s%253D&id=BA2370434CBCF2CF8A22C0FCDFBB15B9&kp=AAR4Kqhc6UKAk2Tl2RsfX33vtgZhGd%2B1%2B%2F1mUPhTkKSg0bLS%2FrGSklIXitXn7IQL7xctUyfBJrssWmgAHCqKTfPADxxm8yJ93S2n6bGUEnWbVQ%3D%3D&nt=5&nw=0&pf=3300&pr=ucpro&sid=621a06ba3e82ee0b0b09827e21c179c3&sv=release&uc_biz_str=OPT%3ABACK_BTN_STYLE%400%7COPT%3ATOOLBAR_STYLE%400%7COPT%3AS_BAR_BG_COLOR%40ffffff%7Cqk_enable_gesture%3Atrue&uc_param_str=dnntnwvepffrgibijbprsvpidsdicheiutkp&ut=AAO3jqGiP6RzKox%2FKmKSp6aQa2lVksVIPKXkS2dt1FDQNg%3D%3D&ve=5.9.3.228&previewShare=previewShare

一致性检验的步骤
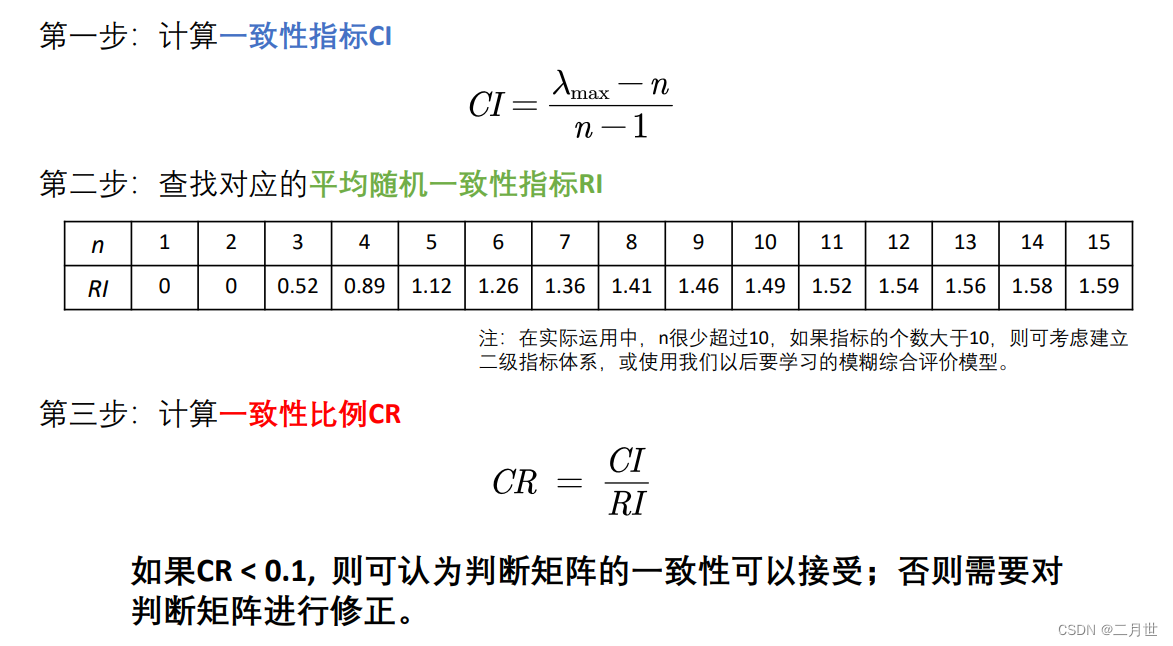

计算判断矩阵
归一化处理
每一行除以其所在列的和
算术平均法求权重
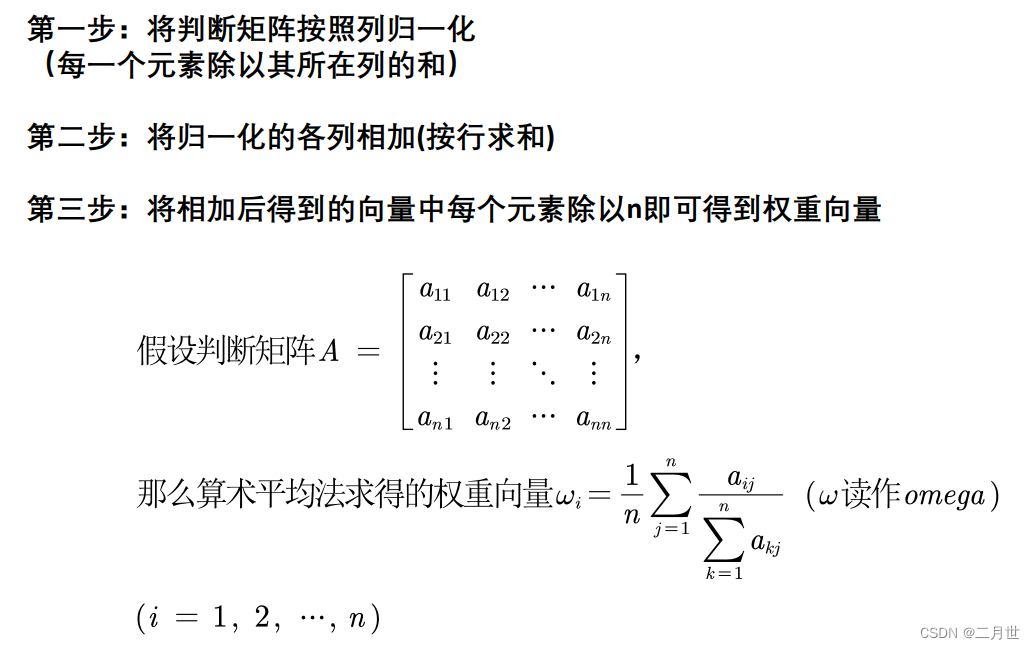
几何平均法求权重
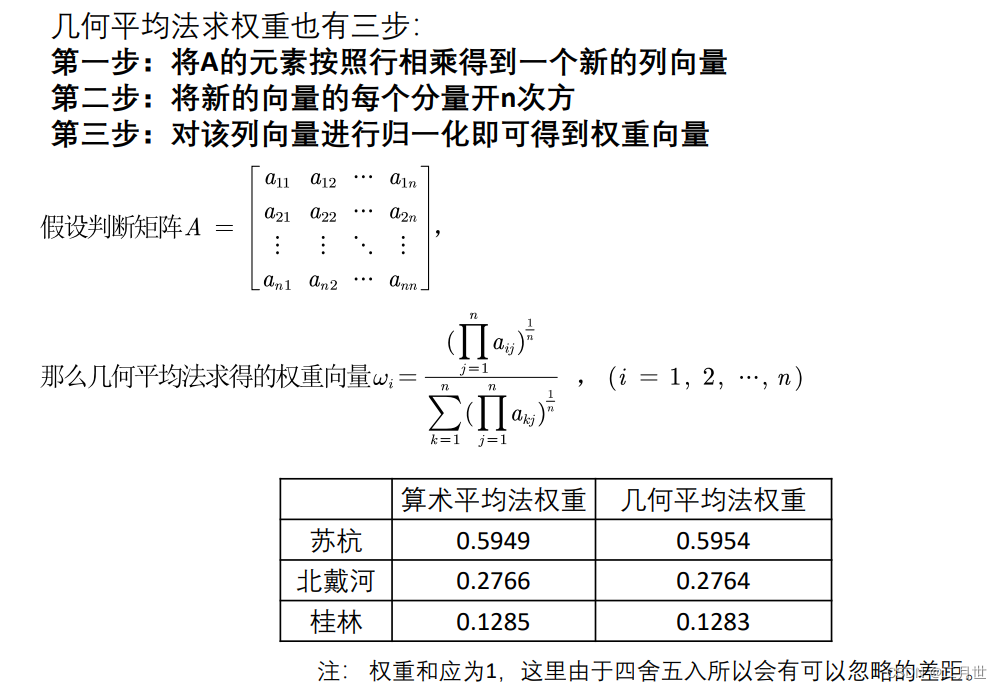
特征值法求权重(常用)


汇总结果,得出结论
得出权重矩阵
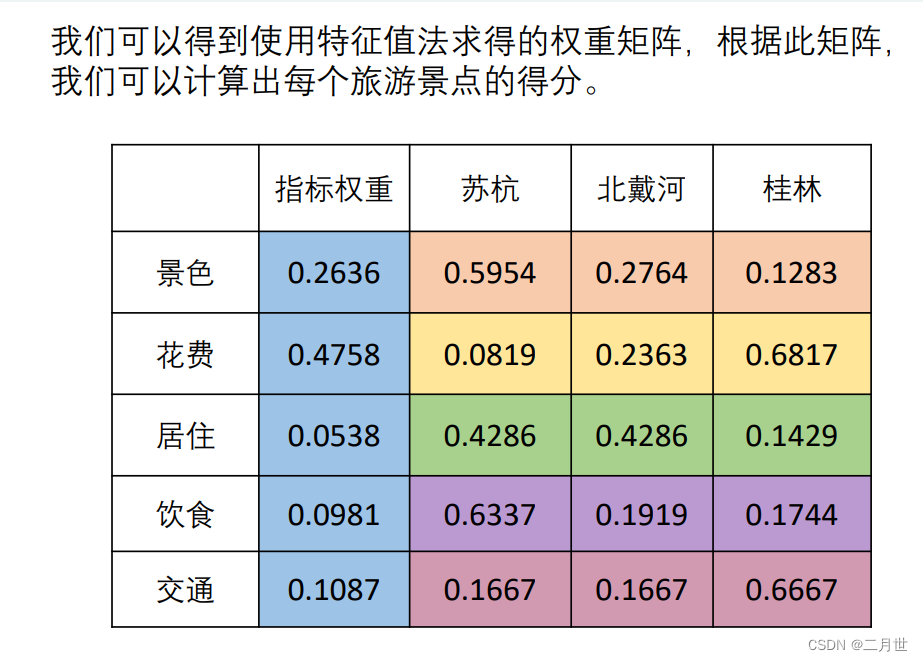
计算得分

在此处使用EXCEL可以简化计算
技巧:F4可以锁定计算用的对应单元格
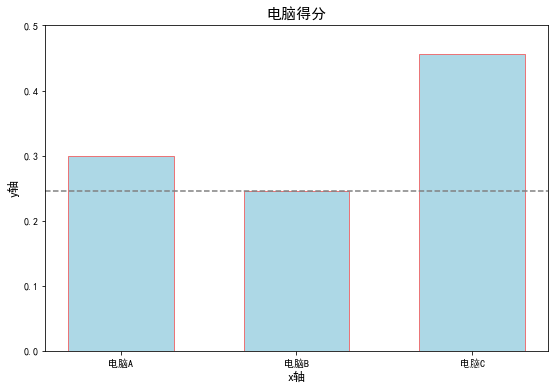
得出结论
比较三者的得分
代码部分
以下代码均来自数模清风课
Matlab入门知识
%% Matlab基本的小常识
% (1)在每一行的语句后面加上分号(一定要是英文的哦;中文的长这个样子;)表示不显示运行结果
a = 3;
a = 5% (2)多行注释:选中要注释的若干语句,快捷键Ctrl+R% (3)取消注释:选中要取消注释的语句,快捷键Ctrl+T% clear可以清楚工作区的所有变量
clear% clc可以清除命令行窗口中的所有文本,让屏幕变得干净
clc% 所以大家在很多代码开头,都会见到:
clear;clc % 分号也用于区分行。
% 这两条一起使用,起到“初始化”的作用,防止之前的结果对新脚本文件(后缀名是 .m)产生干扰。4%% 输出和输入函数(disp 和 input)
% matlab中disp()就是屏幕输出函数,类似于c语言中的printf()函数
disp('我是清风,大家好鸭~~~记得投币关注我哦')
disp(a)
% 注意,disp函数比较特殊,这里可要分号,可不要分号哦
disp(a);% matlab中两个字符串的合并有两种方法
% (1)strcat(str1,str2……,strn) strcat('字符串1','字符串2')
% (2)[str 1,str 2,……, str n]或[str1 str2 …… strn]
['字符串1' '字符串2']
['字符串1','字符串2']
% 一个有用的字符串函数:num2str 将数字转换为字符串
c = 100
num2str(c)
disp(['c的取值为' num2str(c)])
disp(strcat('c的取值为', num2str(c)))% input函数
% 一般我们会将输入的数、向量、矩阵、字符串等赋给一个变量,这里我们赋给A
A = input('请输入A:');
B = input('请输入B:')
% 注意观察工作区,并体会input后面加分号和不加分号的区别%% sum函数
% (1)如果是向量(无论是行向量还是列向量),都是直接求和
E = [1,2,3]
sum(E)
E = [1;2;3]
sum(E)
% (2)如果是矩阵,则需要根据行和列的方向作区分
clc
E = [1,2;3,4;5,6]
% a=sum(x); %按列求和(得到一个行向量)
a = sum(E)
a = sum(E,1)
% a=sum(x,2); %按行求和(得到一个列向量)
a = sum(E,2)
% a=sum(x(:));%对整个矩阵求和
a = sum(sum(E))
a = sum(E(:))%% 基础:matlab中如何提取矩阵中指定位置的元素?
% (1)取指定行和列的一个元素(输出的是一个值)
clc;A=[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1];
A
A(2,1)
A(3,2)
% (2)取指定的某一行的全部元素(输出的是一个行向量)
clc;A
A(2,:)
A(5,:)
% (3)取指定的某一列的全部元素(输出的是一个列向量)
clc;A
A(:,1)
A(:,3)
% (4)取指定的某些行的全部元素(输出的是一个矩阵)
clc;A
A([2,5],:) % 只取第二行和第五行(一共2行)
A(2:5,:) % 取第二行到第五行(一共4行)
A(2:2:5,:) % 取第二行和第四行 (从2开始,每次递增2个单位,到5结束)
1:3:10
10:-1:1
A(2:end,:) % 取第二行到最后一行
A(2:end-1,:) % 取第二行到倒数第二行
% (5)取全部元素(按列拼接的,最终输出的是一个列向量)
clc;A
A(:)%% size函数
clc;
A = [1,2,3;4,5,6]
B = [1,2,3,4,5,6]
size(A)
size(B)
% size(A)函数是用来求矩阵A的大小的,它返回一个行向量,第一个元素是矩阵的行数,第二个元素是矩阵的列数
[r,c] = size(A)
% 将矩阵A的行数返回到第一个变量r,将矩阵的列数返回到第二个变量c
r = size(A,1) %返回行数
c = size(A,2) %返回列数%% repmat函数
% B = repmat(A,m,n):将矩阵A复制m×n块,即把A作为B的元素,B由m×n个A平铺而成。
A = [1,2,3;4,5,6]
B = repmat(A,2,1)
B = repmat(A,3,2)%% Matlab中矩阵的运算
% MATLAB在矩阵的运算中,“*”号和“/”号代表矩阵之间的乘法与除法(A/B = A*inv(B))
A = [1,2;3,4]
B = [1,0;1,1]
A * B
inv(B) % 求B的逆矩阵
B * inv(B)
A * inv(B)
A / B% 两个形状相同的矩阵对应元素之间的乘除法需要使用“.*”和“./”
A = [1,2;3,4]
B = [1,0;1,1]
A .* B
A ./ B% 每个元素同时和常数相乘或相除操作都可以使用
A = [1,2;3,4]
A * 2
A .* 2
A / 2
A ./ 2% 每个元素同时乘方时只能用 .^
A = [1,2;3,4]
A .^ 2
A ^ 2
A * A%% Matlab中求特征值和特征向量
% 在Matlab中,计算矩阵A的特征值和特征向量的函数是eig(A),其中最常用的两个用法:
A = [1 2 3 ;2 2 1;2 0 3]
% (1)E=eig(A):求矩阵A的全部特征值,构成向量E。
E=eig(A)
% (2)[V,D]=eig(A):求矩阵A的全部特征值,构成对角阵D,并求A的特征向量构成V的列向量。(V的每一列都是D中与之相同列的特征值的特征向量)
[V,D]=eig(A)%% find函数的基本用法
% 下面例子来自博客:https://www.cnblogs.com/anzhiwu815/p/5907033.html 博客内有更加深入的探究
% find函数,它可以用来返回向量或者矩阵中不为0的元素的位置索引。
clc;X = [1 0 4 -3 0 0 0 8 6]
ind = find(X)
% 其有多种用法,比如返回前2个不为0的元素的位置:
ind = find(X,2)%上面针对的是向量(一维),若X是一个矩阵(二维,有行和列),索引该如何返回呢?
clc;X = [1 -3 0;0 0 8;4 0 6]
ind = find(X)
% 这是因为在Matlab在存储矩阵时,是一列一列存储的,我们可以做一下验证:
X(4)
% 假如你需要按照行列的信息输出该怎么办呢?
[r,c] = find(X)
[r,c] = find(X,1) %只找第一个非0元素%% 矩阵与常数的大小判断运算
% 共有三种运算符:大于> ;小于< ;等于 == (一个等号表示赋值;两个等号表示判断)
clc
X = [1 -3 0;0 0 8;4 0 6]
X > 0
X == 4%% 判断语句
% Matlab的判断语句,if所在的行不需要冒号,语句的最后一定要以end结尾 ;中间的语句要注意缩进。
a = input('请输入考试分数:')
if a >= 85 disp('成绩优秀')
elseif a >= 60 disp('成绩合格')
elsedisp('成绩挂科')
end% % 注意:代码文件仅供参考,一定不要直接用于自己的数模论文中
% % 国赛对于论文的查重要求非常严格,代码雷同也算作抄袭
本文例题代码计算部分
%% 输入判断矩阵
clear;clc
disp('请输入判断矩阵A: ')
% A = input('判断矩阵A=')
A =[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% matlab矩阵有两种写法,可以直接写到一行:
% [1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 也可以写成多行:
[1 1 4 1/3 3;1 1 4 1/3 3;1/4 1/4 1 1/3 1/2;3 3 3 1 3;1/3 1/3 2 1/3 1]
% 两行之间以分号结尾(最后一行的分号可加可不加),同行元素之间以空格(或者逗号)分开。%% 方法1:算术平均法求权重
% 第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
Sum_A = sum(A)[n,n] = size(A) % 也可以写成n = size(A,1)
% 因为我们的判断矩阵A是一个方阵,所以这里的r和c相同,我们可以就用同一个字母n表示
SUM_A = repmat(Sum_A,n,1) %repeat matrix的缩写
% 另外一种替代的方法如下:SUM_A = [];for i = 1:n %循环哦,这一行后面不能加冒号(和Python不同),这里表示循环n次SUM_A = [SUM_A; Sum_A]end
clc;A
SUM_A
Stand_A = A ./ SUM_A
% 这里我们直接将两个矩阵对应的元素相除即可% 第二步:将归一化的各列相加(按行求和)
sum(Stand_A,2)% 第三步:将相加后得到的向量中每个元素除以n即可得到权重向量
disp('算术平均法求权重的结果为:');
disp(sum(Stand_A,2) / n)
% 首先对标准化后的矩阵按照行求和,得到一个列向量
% 然后再将这个列向量的每个元素同时除以n即可(注意这里也可以用./哦)%% 方法2:几何平均法求权重
% 第一步:将A的元素按照行相乘得到一个新的列向量
clc;A
Prduct_A = prod(A,2)
% prod函数和sum函数类似,一个用于乘,一个用于加 dim = 2 维度是行% 第二步:将新的向量的每个分量开n次方
Prduct_n_A = Prduct_A .^ (1/n)
% 这里对每个元素进行乘方操作,因此要加.号哦。 ^符号表示乘方哦 这里是开n次方,所以我们等价求1/n次方% 第三步:对该列向量进行归一化即可得到权重向量
% 将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为:');
disp(Prduct_n_A ./ sum(Prduct_n_A))%% 方法3:特征值法求权重
% 第一步:求出矩阵A的最大特征值以及其对应的特征向量
clc
[V,D] = eig(A) %V是特征向量, D是由特征值构成的对角矩阵(除了对角线元素外,其余位置元素全为0)
Max_eig = max(max(D)) %也可以写成max(D(:))哦~
% 那么怎么找到最大特征值所在的位置了? 需要用到find函数,它可以用来返回向量或者矩阵中不为0的元素的位置索引。
% 那么问题来了,我们要得到最大特征值的位置,就需要将包含所有特征值的这个对角矩阵D中,不等于最大特征值的位置全变为0
% 这时候可以用到矩阵与常数的大小判断运算
D == Max_eig
[r,c] = find(D == Max_eig , 1)
% 找到D中第一个与最大特征值相等的元素的位置,记录它的行和列。% 第二步:对求出的特征向量进行归一化即可得到我们的权重
V(:,c)
disp('特征值法求权重的结果为:');
disp( V(:,c) ./ sum(V(:,c)) )
% 我们先根据上面找到的最大特征值的列数c找到对应的特征向量,然后再进行标准化。%% 计算一致性比例CR
clc
CI = (Max_eig - n) / (n-1);
RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59]; %注意哦,这里的RI最多支持 n = 15
CR=CI/RI(n);
disp('一致性指标CI=');disp(CI);
disp('一致性比例CR=');disp(CR);
if CR<0.10disp('因为CR < 0.10,所以该判断矩阵A的一致性可以接受!');
elsedisp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end%%注意以上代码,一致性检验在最后,实际上应该提前撰写论文部分
他人的例子(选自2016创新奖B题)

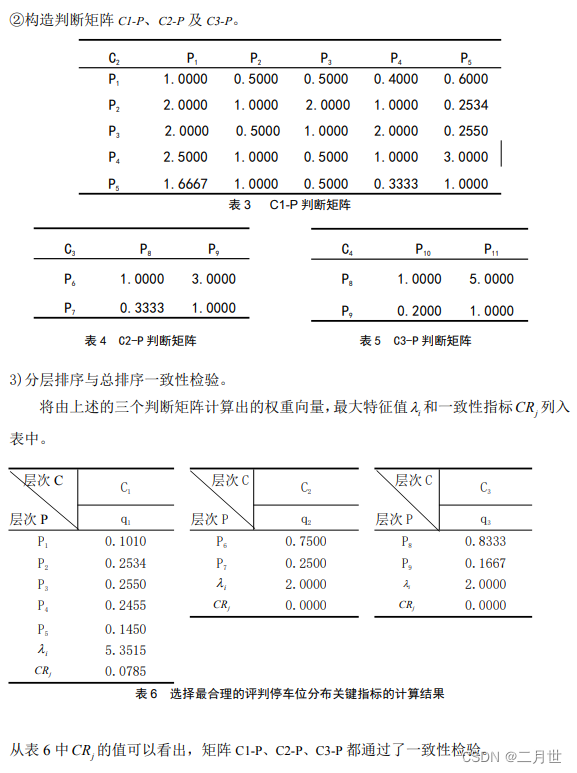
一些技巧
1.在求权重时用三种方法可以避免出错,写进论文里一笔带过可能也会加点评委分。
2.关于作图软件,推荐亿图图示(以本文题例) 
3.若没有通过一致性检验则需要对假设的数据进行调整,向判断矩阵行列成比例上调整
4.评价层标准不宜太多,太多可能会导致一致性检验难以通过。若N为2,可以把表中2对应数据近似为0.001来代入公式。
5.在excel用公式计算单元格之间的值时,按F4可以锁定公式中锁定的单元格,有助于将公式推广到此后的单元格