离散模型:代数方程与差方程、整数规划、图论、对策论、网络论
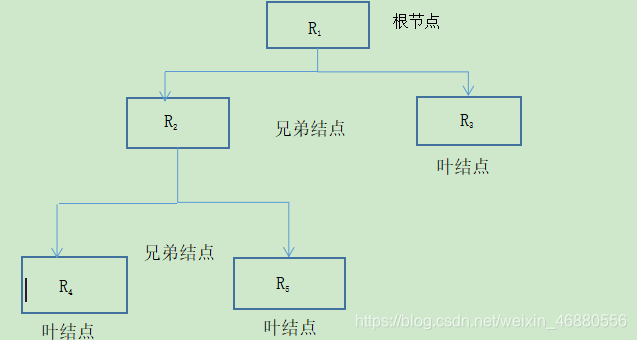
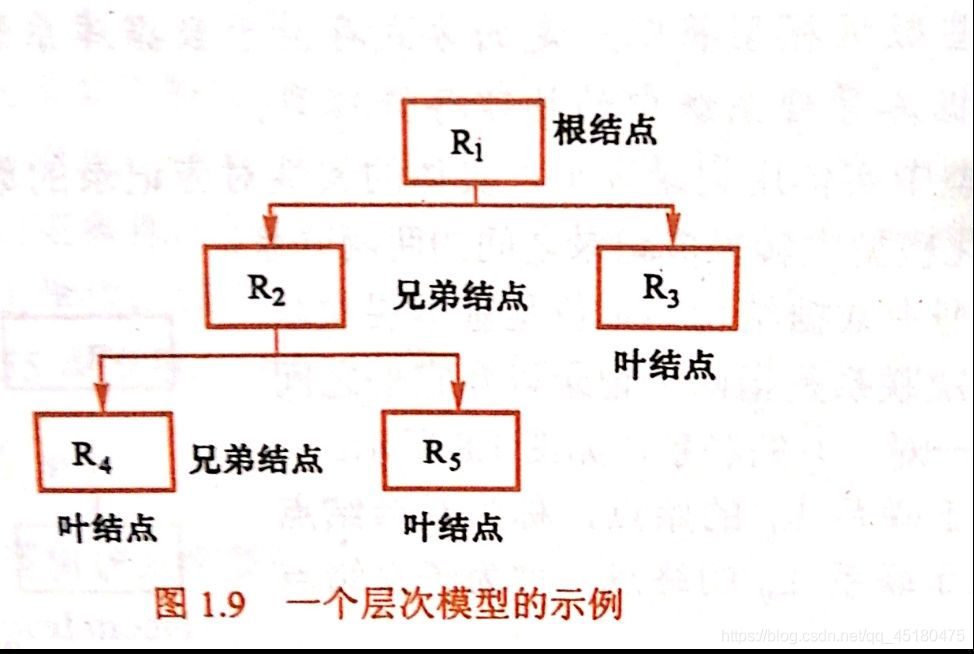
层次模型(AHP)是一种定性与定量相结合的、系统化、层次化的分析方法。
人们在进行社会的、经济的以及科学管理领域问题的系统分析中,面临的常常是一个互相关联、相互制约的众多元素构成复杂而往往缺少定量数据的系统
- 建立阶梯层次结构模型
- 构造出各层次中的所有判断矩阵
- 层次单排序及一致性检验
- 层次总排序及一致性检验
阶梯层次结构的建立与特点
复杂问题被分解为元素的组成部分。这些元素按其属性及关系形成若干层次。上一层次的元素作为准则对下一层次有关元素起支配作用。
层次可以大致分为三类:
- 最高层
在一层次中只有一个元素。一般是它分析问题的预定目标或理想结果,因此也称为目标层 - 中间层
这一层次中包含了为实现目标所涉及的中间环节,它可以由若干个层次组成,包括所需要的准则、子准则,因此也称为准则层 - 最底层
这一层包括了为实现目标可供选择的各种措施、决策方案等,因此也称为措施层或方案层
层次分析法的基本步骤:如何在3个目的地中按照景色、费用、居住条件等因素选择
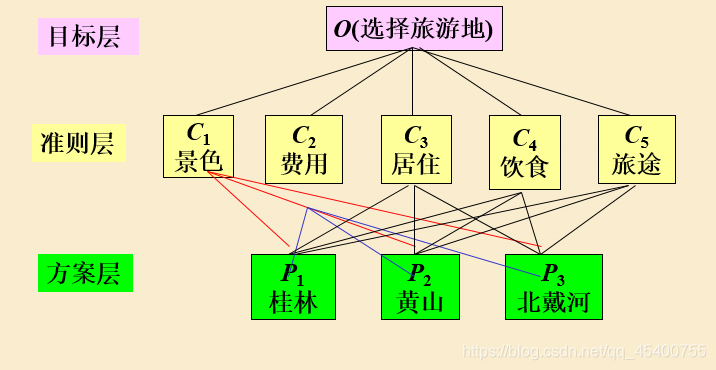
思维归纳:
- 将决策问题分为3个层次:目标层,准则层、方案层;每层有若干元素,各层元素间的关系用相连的直线表示
- 通过互相比较确定各准则对目标的权重,以及方案对每一准则的权重
- 将上述两组权重进行综合,确定各方案对目标的权重
构造判断矩阵
层次结构反映了因素之间大的关系,但准则层中的各准则在目标衡量中所占的比重并不一定相同,在决策者心中,它们所占有一定的比例
在确定影响某因素的诸因子在该因素中所占的比重时,遇到主要困难是这些比重常常不易定量化。此外,当影响某因素的因子较多时,直接考虑各因子对该因素有多大程度的影响时,常常会因考虑不周、顾此失彼而使决策者提出与他实际认为的可作重要性程度不相一致的数据



层次单排序及一致性检验
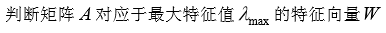
经归一化后即为同一层次相应因素对于上一层次某因素相对重要性的排序权值,这一过程被称为单排序。
上述构造对比较判断的办法虽能减少其他因素的干扰,较客观地反映出一对因素对于上一层次某因素影响力的差别。
成对比较阵和权向量
成对比较完全一致性的情况满足aij.ajk=aik,i,j,k=1,2,…,n的正互反阵A称一致阵
A的秩为1,A的唯一非零特征根为n
A的任一列向量是对应于n的特征向量
A的归一化特征向量可作为权向量
一致性检验: