前言

二叉树一遍有前序、中序和后序三种遍历方式，不同的遍历方式有不同的用处。
二叉树遍历都是先左后右的。
二叉树类：

public class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode() {}public TreeNode(int val) {this.val = val;}public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}

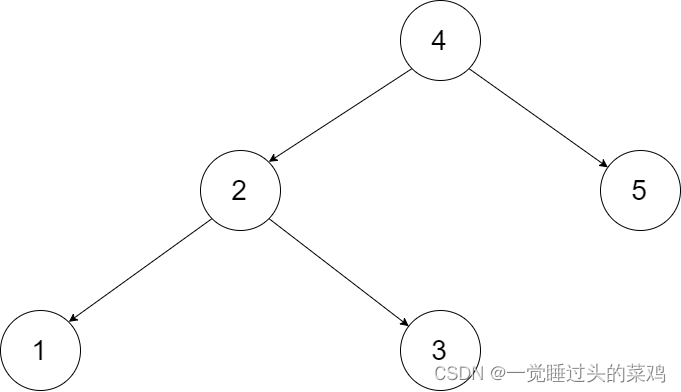
在这里插入图片描述
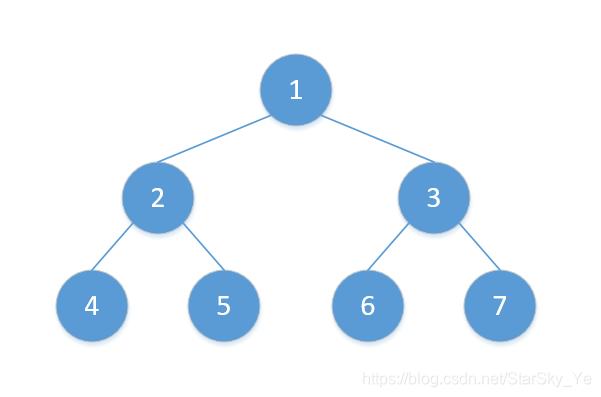
构建这颗树：

        TreeNode root = new TreeNode(4);TreeNode temp1 = new TreeNode(1);TreeNode temp2 = new TreeNode(2);TreeNode temp3 = new TreeNode(3);TreeNode temp5 = new TreeNode(5);root.left = temp2;root.right = temp5;temp2.right = temp3;temp2.left = temp1;

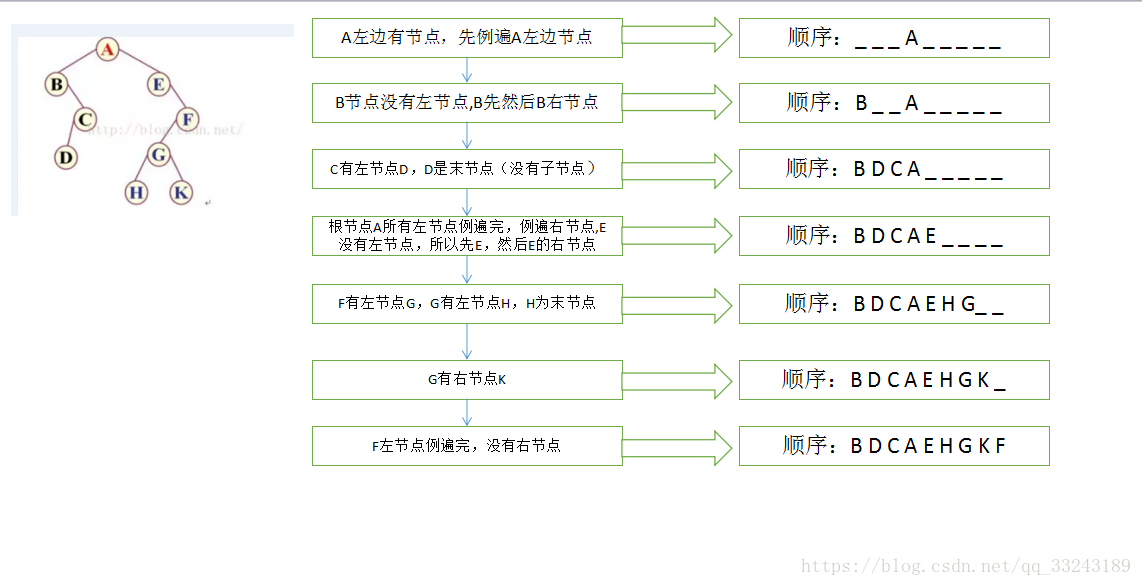
一、前序

1. 中左右进行遍历：

遍历根节点
遍历根节点的左节点（如果左节点不是叶子节点，则以当前节点开始，重新从第一步开始）
遍历根节点的右节点（如果右节点不是叶子节点，则以当前节点开始，重新从第一步开始）

2. 代码实现

    public void pre(TreeNode root) {if (root == null)return;System.out.print(root.val);pre(root.left);pre(root.right);}

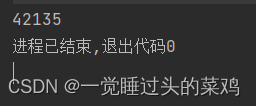
结果为42135
在这里插入图片描述

二、中序

1. 左中右进行遍历

遍历根节点的左节点（如果左节点不是叶子节点，则以当前节点开始，重新从第一步开始）
遍历根节点
遍历根节点的右节点（如果右节点不是叶子节点，则以当前节点开始，重新从第一步开始）

2. 代码实现

    public static void cur(TreeNode root) {if (root == null)return;cur(root.left);System.out.print(root.val);cur(root.right);}

结果为：12345
在这里插入图片描述

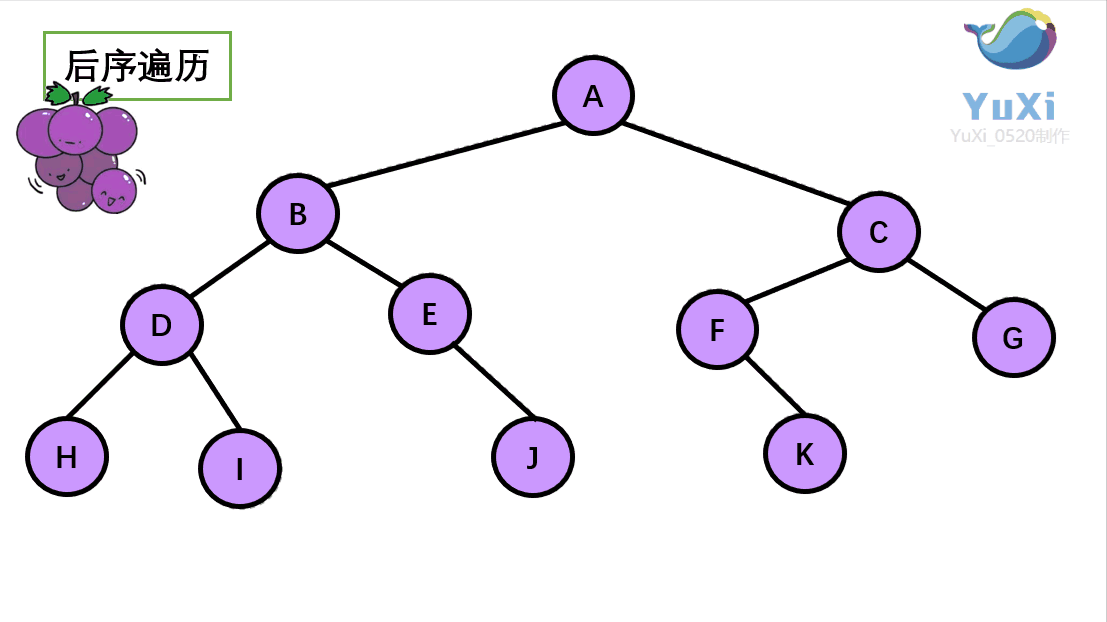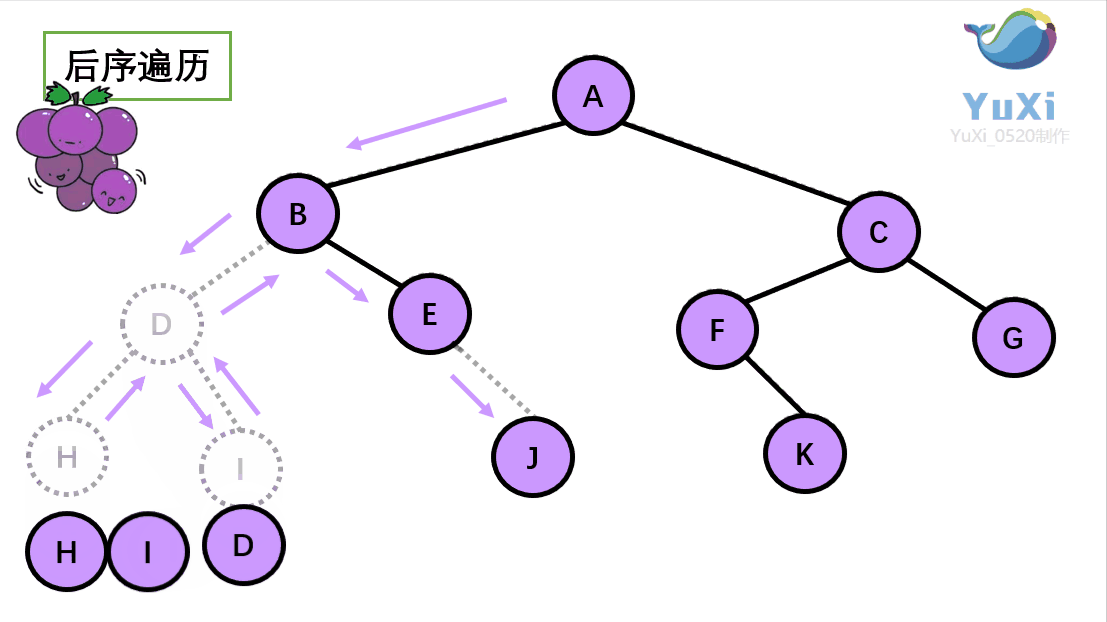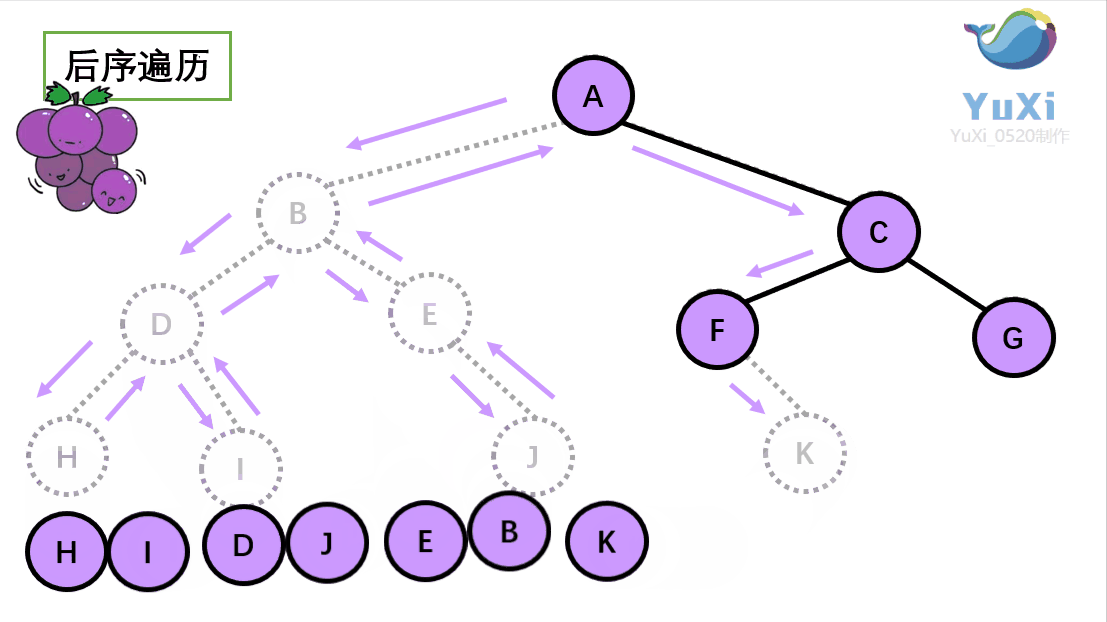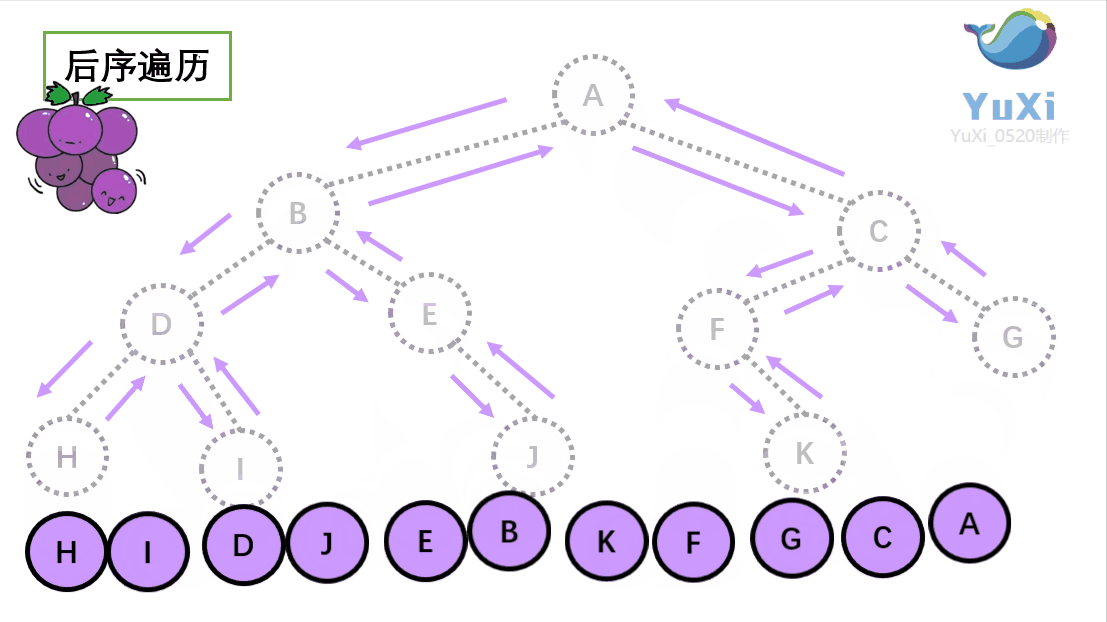
三、后序

1. 左右中进行遍历

遍历根节点的左节点（如果左节点不是叶子节点，则以当前节点开始，重新从第一步开始）
遍历根节点的右节点（如果右节点不是叶子节点，则以当前节点开始，重新从第一步开始）
遍历根节点

2. 代码实现

    public static void nxt(TreeNode root) {if (root == null)return;nxt(root.left);nxt(root.right);System.out.print(root.val);}

结果为：13254
在这里插入图片描述

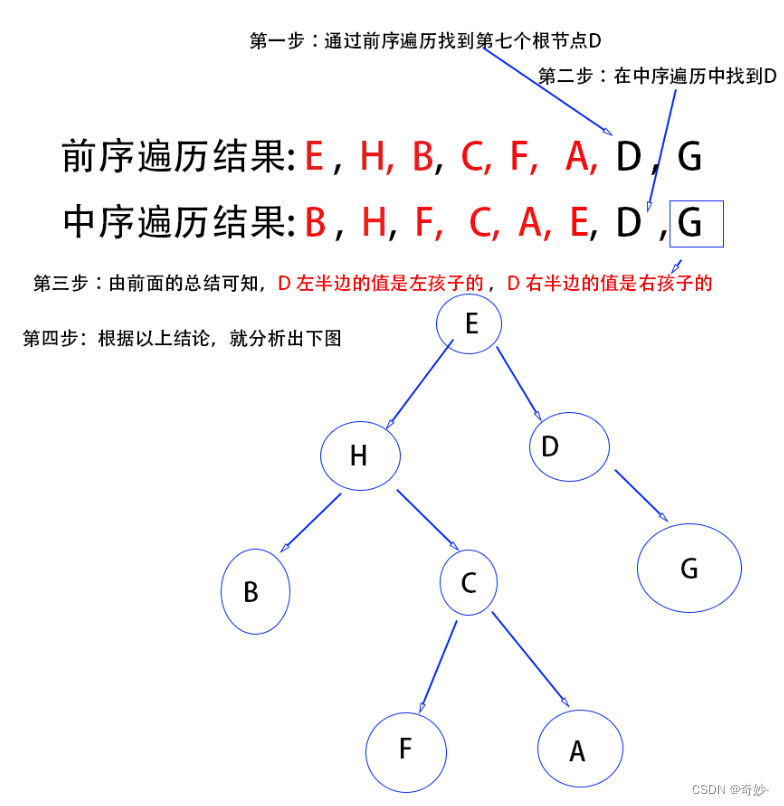
四、逆推二叉树

前序加中序可以逆推二叉树；

	//记录前序中的位置int key = 0;public TreeNode buildTree(int[] preorder, int[] inorder) {return function(preorder,inorder,0,inorder.length - 1);}public TreeNode function(int[] preorder, int[] inorder,int left,int right){if (left == right){TreeNode node = new TreeNode(preorder[key]);key++;return node;} else if (left > right)return null;int rootIndex = 0;for (int i = left; i <= right; i++) {if (inorder[i] == preorder[key]){rootIndex = i;break;}}TreeNode node = new TreeNode(preorder[key]);key++;node.left = function(preorder,inorder,left,rootIndex - 1);node.right = function(preorder, inorder, rootIndex+1, right);if (node.left == node.right)key--;return node;}