前言

最近复习题中看到二叉树，对于它的前序，中序，后序遍历的判断有些模糊，后经查阅资料，将学习过程记录在博客中。

提示：以下是本篇文章正文内容

一、如何判断二叉树的前序，中序，后序遍历？

对一棵二叉树进行遍历，我们可以采取3中顺序进行遍历，分别是前序遍历、中序遍历和后序遍历。这三种方式是以访问父节点的顺序来进行命名的。假设根节点是N，左节点是L，右节点是R，那么对应的访问遍历顺序如下：

前序遍历 N（根节点）－>L（左节点）－>R （右节点）
中序遍历 L（左节点）－>N（根节点）－>R （右节点）
后序遍历 L（左节点）－>R（右节点）－>N （根节点）

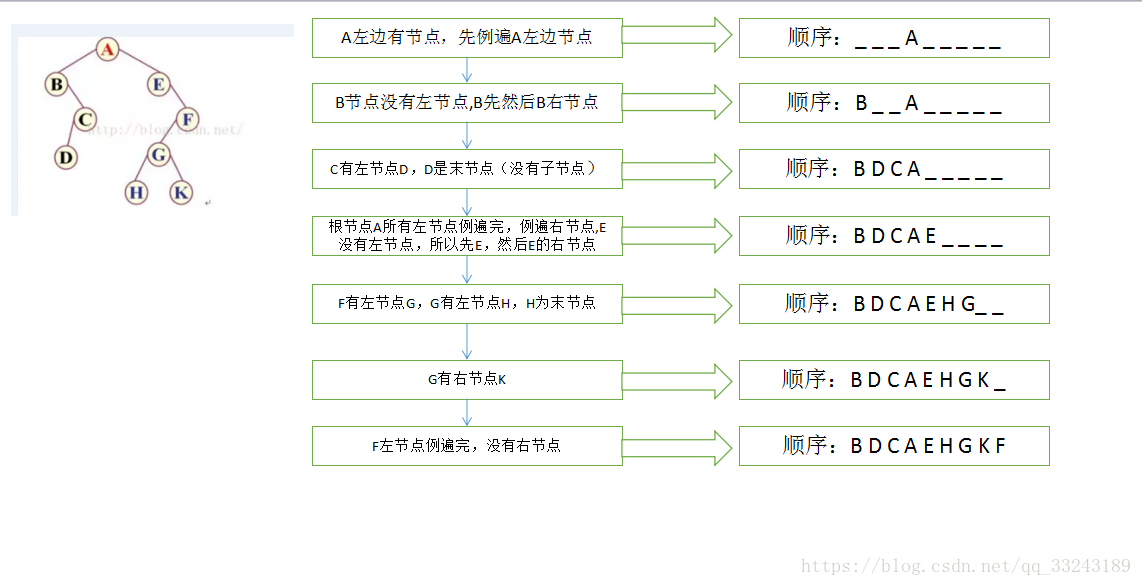
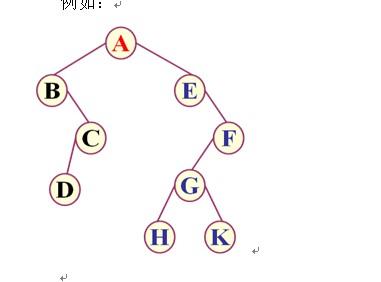
所以，对于以下这棵树，三种遍历方式的结果是：

在这里插入图片描述

前序遍历 ABCDEF
中序遍历 CBDAEF
后序遍历 CDBFEA

如果还是不明白怎样判断的，那么下面是详细描述

二、已知二叉树的前序遍历和中序遍历，如何得到它的后序遍历？

其实，只要知道其中任意两种遍历的顺序，我们就可以推断出剩下的一种遍历方式的顺序，这里我们只是以：知道前序遍历和中序遍历，推断后序遍历作为例子，其他组合方式原理是一样的。要完成这个任务，我们首先要利用以下四个特性：

特性1，对于前序遍历，第一个肯定是根节点；
特性2，对于后序遍历，最后一个肯定是根节点；
特性3，利用前序或后序遍历，确定根节点，在中序遍历中，根节点的两边就可以分出左子树和右子树；
特性4，对左子树和右子树分别做前面3点的分析和拆分，相当于做递归，我们就可以重建出完整的二叉树；

范例如下（示例）：

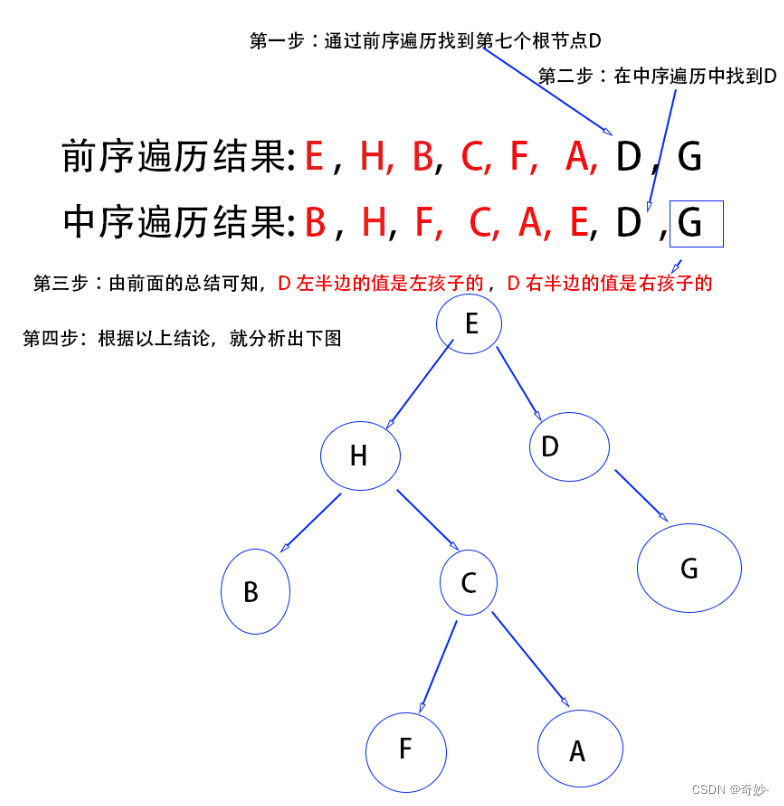
我们以一个例子做一下这个过程，假设：
前序遍历的顺序是: CABGHEDF
中序遍历的顺序是: GHBACDEF第一步,我们根据特性1,可以得知根节点是C,然后,根据特性3,我们知道左子树是:GHBA,右子树是:DEFC/     \GHBA      DEF
第二步,取出左子树,左子树的前序遍历是:ABGH,中序遍历是:GHBA(从上面题目中得出)
根据特性1和3,得出左子树的根节点是A,并且A没有右子树。C/     \A        DEF/GHB
第三步,使用同样的方法,前序是BGH,中序是GHB,得出根节点是B,GH为B的左子树,并且B没有右子树。
再看前序中GH,G在H的前面,也就是说,G是先前序遍历访问的,则得到H是G的左子树C/     \A        DEF/B/    G / H     第四步,回到右子树,它的前序是EDF,中序是DEF,依然根据特性1和3,得出根节点是E,左节点是D,右节点为F。C/     \A        E/        /    \B         D      F/    G / H     到此,我们得到了这棵完整的二叉树,因此,它的后序遍历就是:HGBADFEC

三、程序实现

下面我们使用程序来实现根据前序遍历和中序遍历得到后续遍历。
首先我们需要建立节点的实体类：

/*** 二叉树的节点数据结构*/
public class TreeNode {private String key = null;private String data = null;public boolean isVisted = false;/*** 左儿子节点*/public TreeNode leftChild = null;/*** 右儿子节点*/public TreeNode rightChild = null;/*** 默认构造方法*/public TreeNode(){}/*** @param key  层序编码* @param data 数据域*/public TreeNode(String key, String data){this.setKey(key);this.setData(data);this.leftChild = null;this.rightChild = null;}/*** 序号*/public String getKey() {return key;}public void setKey(String key) {this.key = key;}/*** 值*/public String getData() {return data;}public void setData(String data) {this.data = data;}
}

具体实现代码

/*** 给出前序遍历和终须遍历，求得二叉树及后续遍历* Created by sschen on 17/5/2.** 前序遍历    N－>L－>R* 中序遍历    L－>N－>R* 后序遍历    L－>R－>N** 特性A，对于前序遍历，第一个肯定是根节点；* 特性B，对于后序遍历，最后一个肯定是根节点；* 特性C，利用前序或后序遍历，确定根节点，在中序遍历中，根节点的两边就可以分出左子树和右子树；* 特性D，对左子树和右子树分别做前面3点的分析和拆分，相当于做递归，我们就可以重建出完整的二叉树；*/
public class BinaryTreeFind {public static void main(String[] args) {/***             A*          /        \*        B           C*      /     \          \*     D       E          F*   /        /  \           \*  G        H    I            J*   \      /*    K    L** 前序遍历： ABDGKEHLICFJ* 中序遍历； GKDBLHEIACFJ* 后续遍历： KGDLHIEBJFCA*/String pr = "ABDGKEHLICFJ";String in = "GKDBLHEIACFJ";TreeNode node = GetTree(pr, in, "root");postOrder(node);}/*** 递归计算节点列表* @param pr 前序遍历字符串* @param in 中序遍历字符串* @param index 层级序号* @return 节点*/private static TreeNode GetTree(String pr, String in, String index){if (pr == "" || in == "") {//如果字符串为空直接返回空值return null;}//前序遍历的第一个节点必然是该段根节点String firstNodeValue = pr.substring(0, 1);TreeNode node = new TreeNode(index, firstNodeValue);if (in.length() == 1) {//中序遍历没有节点了，直接返回自身return node;}//得到跟节点在中序遍历中的位置int iLeftLength = in.indexOf(firstNodeValue);if (iLeftLength == 0) {//已经是中序遍历的第一个元素，则代表没有左儿子node.leftChild = null;}else {node.leftChild = GetTree(pr.substring(1, iLeftLength + 1), in.substring(0, iLeftLength),index + "-L");}if (iLeftLength == in.length() - 1) {//已经是中序遍历的最后一个节点，代表没有右儿子node.rightChild = null;}else {node.rightChild = GetTree(pr.substring(iLeftLength + 1), in.substring(iLeftLength + 1),index + "-R");}return node;}/*** 对二叉树进行后续遍历* @param subTree 二叉树*/public static void postOrder(TreeNode subTree) {if (subTree != null) {postOrder(subTree.leftChild);postOrder(subTree.rightChild);visted(subTree);}}public static void visted(TreeNode subTree){subTree.isVisted=true;System.out.println("key:" + subTree.getKey() + "--name:" + subTree.getData());;}
}

执行结果为

key:root-L-L-L-R--name:K
key:root-L-L-L--name:G
key:root-L-L--name:D
key:root-L-R-L-L--name:L
key:root-L-R-L--name:H
key:root-L-R-R--name:I
key:root-L-R--name:E
key:root-L--name:B
key:root-R-R-R--name:J
key:root-R-R--name:F
key:root-R--name:C
key:root--name:A