该楼层疑似违规已被系统折叠 隐藏此楼查看此楼
%三边测量的定位算法
%dA,dB,dC为A,B,C到未知节点(假定坐标[x,y]未知)的模拟测量距离
A = [0,0];
B = [25,25*sqrt(3)];
C = [50,0];
dA=51/sqrt(3);
dB=51/sqrt(3);
dC=51/sqrt(3);
%A,B,C为三个选定的信标节点,节点坐标已知(为便于防真及验证,代码中采用的等边三角形)
%定义未知坐标x,y为符号变量
syms x y;
%距离方程,以信标节点为圆心,信标节点到未知节点的测量距离为半径作三个圆
f1 = (A(1)-x)^2+(A(2)-y)^2-dA^2;
f2 = (B(1)-x)^2+(B(2)-y)^2-dB^2;
f3 = (C(1)-x)^2+(C(2)-y)^2-dC^2;
%任两个方程联立,求任两圆交点
s1 = solve(f1,f2); %求A,B两圆的交点
s2 = solve(f2,f3); %求B,C两圆的交点
s3 = solve(f1,f3); %求A,C两圆的交点
%将结果(符号变量)转换为双精度数值
x1 = double(s1.x);
y1 = double(s1.y);
x2 = double(s2.x);
y2 = double(s2.y);
x3 = double(s3.x);
y3 = double(s3.y);
%选择内侧的三个交点
%两圆相交于两点,距第三个圆心近的为选定交点Pab,Pbc,Pac
d1(1) = sqrt(((C(1)-x1(1))^2+(C(2)-y1(1))^2));
d1(2) = sqrt(((C(1)-x1(2))^2+(C(2)-y1(2))^2));
if d1(1) <= d1(2)
Pab(1) = x1(1);
Pab(2) = y1(1);
else
Pab(1) = x1(2);
Pab(2) = y1(2);
end
d2(1) = sqrt(((A(1)-x2(1))^2+(A(2)-y2(1))^2));
d2(2) = sqrt(((A(1)-x2(2))^2+(A(2)-y2(2))^2));
if d2(1) <= d2(2)
Pbc(1) = x2(1);
Pbc(2) = y2(1);
else
Pbc(1) = x2(2);
Pbc(2) = y2(2);
end
d3(1) = sqrt(((B(1)-x3(1))^2+(B(2)-y3(1))^2));
d3(2) = sqrt(((B(1)-x3(2))^2+(B(2)-y3(2))^2));
if d3(1) <= d3(2)
Pac(1) = x3(1);
Pac(2) = y3(1);
else
Pac(1) = x3(2);
Pac(2) = y3(2);
end
%求三个圆内侧三个交点Pab,Pbc,Pac的质心,即为未知节点P,完成定位
P(1) = (Pab(1)+Pbc(1)+Pac(1))/3;
P(2) = (Pab(2)+Pbc(2)+Pac(2))/3;
转为c的代码如下
编译链接环境VC6.0
代码如下:
//三边测量的定位算法
//dA,dB,dC为A,B,C到未知节点(假定坐标[x,y]未知)的模拟测量距离
#include
#include
struct point_t
{
double x;
double y;
};
struct circle_t
{
struct point_t center;//圆心
double r;//半径
};
int double_equals(double const a, double const b)
{
static const double ZERO = 1e-9;
return fabs(a - b) < ZERO;
}
double distance_sqr(struct point_t const* a, struct point_t const* b)
{
return (a->x - b->x) * (a->x - b->x) + (a->y - b->y) * (a->y - b->y);
}
double distance(struct point_t const* a, struct point_t const* b)
{
return sqrt(distance_sqr(a, b));
}
double distance_pow(double x1,double y1,double x2,double y2)
{
return pow((x1-x2),2) + pow((y1-y2),2);
}
int insect(struct circle_t circles[], struct point_t points[])
{
double d, a, b, c, p, q, r;
double cos_value[2], sin_value[2];
if (double_equals(circles[0].center.x, circles[1].center.x)
&& double_equals(circles[0].center.y, circles[1].center.y)
&& double_equals(circles[0].r, circles[1].r))
{
return -1;
}
d = distance(&circles[0].center, &circles[1].center);
if (d > circles[0].r + circles[1].r
|| d < fabs(circles[0].r - circles[1].r))
{
return 0;
}
a = 2.0 * circles[0].r * (circles[0].center.x - circles[1].center.x);
b = 2.0 * circles[0].r * (circles[0].center.y - circles[1].center.y);
c = circles[1].r * circles[1].r - circles[0].r * circles[0].r
- distance_sqr(&circles[0].center, &circles[1].center);
p = a * a + b * b;
q = -2.0 * a * c;
if (double_equals(d, circles[0].r + circles[1].r)
|| double_equals(d, fabs(circles[0].r - circles[1].r))){
cos_value[0] = -q / p / 2.0;
sin_value[0] = sqrt(1 - cos_value[0] * cos_value[0]);
points[0].x = circles[0].r * cos_value[0] + circles[0].center.x;
points[0].y = circles[0].r * sin_value[0] + circles[0].center.y;
if (!double_equals(distance_sqr(&points[0], &circles[1].center),circles[1].r * circles[1].r))
{
points[0].y = circles[0].center.y - circles[0].r * sin_value[0];
}
return 1;
}
r = c * c - b * b;
cos_value[0] = (sqrt(q * q - 4.0 * p * r) - q) / p / 2.0;
cos_value[1] = (-sqrt(q * q - 4.0 * p * r) - q) / p / 2.0;
sin_value[0] = sqrt(1 - cos_value[0] * cos_value[0]);
sin_value[1] = sqrt(1 - cos_value[1] * cos_value[1]);
points[0].x = circles[0].r * cos_value[0] + circles[0].center.x;
points[1].x = circles[0].r * cos_value[1] + circles[0].center.x;
points[0].y = circles[0].r * sin_value[0] + circles[0].center.y;
points[1].y = circles[0].r * sin_value[1] + circles[0].center.y;
if (!double_equals(distance_sqr(&points[0], &circles[1].center),circles[1].r * circles[1].r))
{
points[0].y = circles[0].center.y - circles[0].r * sin_value[0];
}
if (!double_equals(distance_sqr(&points[1], &circles[1].center),circles[1].r * circles[1].r))
{
points[1].y = circles[0].center.y - circles[0].r * sin_value[1];
}
if (double_equals(points[0].y, points[1].y)&& double_equals(points[0].x, points[1].x))
{
if (points[0].y > 0)
{
points[1].y = -points[1].y;
}
else
{
points[0].y = -points[0].y;
}
}
return 2;
}
void main()
{
point_t Pab;
point_t Pbc;
point_t Pac;
point_t A;
point_t B;
point_t C;
double dA,dB,dC;
A.x = 0.0; //圆心
A.y = 0.0;
B.x = 25.0; //圆心
B.y = 25.0*sqrt(3);
C.x = 50.0; //圆心
C.y = 0.0;
dA = 51.0/sqrt(3);//半径
dB = 51.0/sqrt(3);//半径
dC = 51.0/sqrt(3);//半径
//A,B,C为三个选定的信标节点,节点坐标已知(为便于防真及验证,代码中采用的等边三角形)
//定义未知坐标x,y为符号变量
//距离方程,以信标节点为圆心,信标节点到未知节点的测量距离为半径作三个圆
struct circle_t circles_AB[2];
struct point_t points_AB[2];
circles_AB[0].center.x = A.x;
circles_AB[0].center.y = A.y;
circles_AB[0].r = dA;
circles_AB[1].center.x = B.x;
circles_AB[1].center.y = B.y;
circles_AB[1].r = dB;
switch (insect(circles_AB, points_AB))
{
case -1:
printf("THE CIRCLES ARE THE SAME\n");
break;
case 0:
printf("NO INTERSECTION\n");
break;
case 1:
printf("(%.3lf %.3lf)\n", points_AB[0].x, points_AB[0].y);
break;
case 2:
printf("求A,B两圆的交点为\n");
printf("(%.3lf %.3lf) (%.3lf %.3lf)\n",points_AB[0].x, points_AB[0].y,
points_AB[1].x, points_AB[1].y);
}
//printf("(%.3lf %.3lf %.3lf)\n", A.x, A.y,dA);
//printf("(%.3lf %.3lf %.3lf)\n", B.x, B.y,dA);
//printf("(%.3lf %.3lf %.3lf)\n", C.x, C.y,dA);
double points_AB_0 = distance_pow(points_AB[0].x,points_AB[0].y,C.x,C.y);
double points_AB_1 = distance_pow(points_AB[1].x,points_AB[1].y,C.x,C.y);
if(points_AB_0 < points_AB_1)
{
Pab.x = points_AB[0].x;
Pab.y = points_AB[0].y;
}
else
{
Pab.x = points_AB[1].x;
Pab.y = points_AB[1].y;
}
struct circle_t circles_BC[2];
struct point_t points_BC[2];
circles_BC[0].center.x = B.x;
circles_BC[0].center.y = B.y;
circles_BC[0].r = dB;
circles_BC[1].center.x = C.x;
circles_BC[1].center.y = C.y;
circles_BC[1].r = dC;
switch (insect(circles_BC, points_BC))
{
case -1:
printf("THE CIRCLES ARE THE SAME\n");
break;
case 0:
printf("NO INTERSECTION\n");
break;
case 1:
printf("(%.3lf %.3lf)\n", points_BC[0].x, points_BC[0].y);
break;
case 2:
printf("求B,C两圆的交点为\n");
printf("(%.3lf %.3lf) (%.3lf %.3lf)\n",points_BC[0].x, points_BC[0].y,
points_BC[1].x, points_BC[1].y);
}
double points_BC_0 = distance_pow(points_BC[0].x,points_BC[0].y,A.x,A.y);
double points_BC_1 = distance_pow(points_BC[1].x,points_BC[1].y,A.x,A.y);
if(points_BC_0 < points_BC_1)
{
Pbc.x = points_BC[0].x;
Pbc.y = points_BC[0].y;
}
else
{
Pbc.x = points_BC[1].x;
Pbc.y = points_BC[1].y;
}
struct circle_t circles_AC[2];
struct point_t points_AC[2];
circles_AC[0].center.x = A.x;
circles_AC[0].center.y = A.y;
circles_AC[0].r = dA;
circles_AC[1].center.x = C.x;
circles_AC[1].center.y = C.y;
circles_AC[1].r = dC;
switch (insect(circles_AC, points_AC))
{
case -1:
printf("THE CIRCLES ARE THE SAME\n");
break;
case 0:
printf("NO INTERSECTION\n");
break;
case 1:
printf("(%.3lf %.3lf)\n", points_AC[0].x, points_AC[0].y);
break;
case 2:
printf("求A,C两圆的交点为\n");
printf("(%.3lf %.3lf) (%.3lf %.3lf)\n",points_AC[0].x, points_AC[0].y,
points_AC[1].x, points_AC[1].y);
}
double points_AC_0 = distance_pow(points_AC[0].x,points_AC[0].y,B.x,B.y);
double points_AC_1 = distance_pow(points_AC[1].x,points_AC[1].y,B.x,B.y);
if(points_AC_0 < points_AC_1)
{
Pac.x = points_AC[0].x;
Pac.y = points_AC[0].y;
}
else
{
Pac.x = points_AC[1].x;
Pac.y = points_AC[1].y;
}
double P_1,P_2;
P_1 = (Pab.x + Pbc.x + Pac.x)/3.0;
P_2 = (Pab.y + Pbc.y + Pac.y)/3.0;
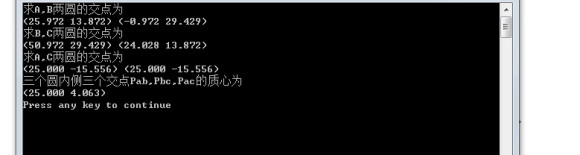
printf("三个圆内侧三个交点Pab,Pbc,Pac的质心为\n");
printf("(%.3lf %.3lf)\n", P_1, P_2);
}