在有向图中找出所有简单环--Johnson算法

article/2025/9/25 18:55:38

注：本算法和计算图所有结点对最短路径的Johnson算法不同。

综述

Johnson算法由B. Johnson发表于1975年，用于在一个有向图中寻找所有简单环。时间复杂度上界为O((n+e)(c+1))，空间复杂度为O(n+e)，其中n为顶点数，e为边数，c为存在环数。在算法执行时，每两个连续的环的输出之间的时间不会超过O(n+e)。

*常用的此类算法的复杂度比较如下：

Tiernan - O(V.const^V)
Tarjan - O(VEC)
Johnson - O(((V+E)C)
Szwarcfiter and Lauer - O(V+EC)

所谓的简单环，即除了第一个和最后一个顶点，其余所有顶点在路径中只出现一次。这里排除了包括像v->v这样的自循环的边和在两个顶点之间的多条边的情况。本算法沿用Tiernan算法的记号，每个简单环都是由根顶点为s的子图构建的，这个子图由s和“大于”s的顶点构成。因此每个输出都根据路径的最小点s来分类。

当从s开始遍历路径，把一个顶点v加入这个路径时，会把这个顶点的状态设为“阻塞”（blocked），直到从v到s的所有路径都完成检索，v会一直保持这种状态，这样保证了一个顶点不会被重复添加。另外除非一个顶点是构造简单环路径的最小的点，这个点不会成为路径的根顶点。这样保证不会无意义的搜索。

算法的输入是一个图结构，图的表示是邻接表形式。假设每个顶点用从1到n的一个数字表示，图表示为AG，则AG(v)是一个数组表示第v个顶点的邻接顶点。算法的过程是这样的：从一个根顶点s开始构建简单环，所经过的路径的顶点保存在一个栈中。算法通过调用CIRCUIT过程添加新顶点，添加时务必将其设置为blocked，并且在过程调用返回时删除这个顶点，但是此时不一定将其阻塞状态去除。

代码解析

下面是算法的伪代码：

algo

如上所述，整个算法包括CIRCUIT主过程，位于empty stack;语句以上，它又包含一个子过程UNBLOCK用于对一个blocked顶点进行解锁。下面以C++为例谈一下我对这个算法实现的理解：

每个点的ID表示为1到n的一个类型为size_t整数。Ak，B两个数组在开始时被初始化，数组的长度都为n，即顶点数目。这两个数组的元素都是list<size_t>，A数组第i个元素的链表记录从点i出发指向的顶点，即图的邻接表。B的作用是记录因为此点阻塞而被迫阻塞的顶点，一旦点i因为调用unblock过程解锁，那么在B[i]链表中记录的顶点也因此解锁。B的效果是将每个点尽可能的保持阻塞状态以防止重复搜索。blocked是一个长度为n的bool数组，表示在搜索时这个点是否是阻塞。s表示目前搜索到的根结点的编号。

CIRCUIT过程从stack v;语句开始，其输入参数v表示这个CIRCUIT过程所搜索的环都是从v这个顶点开始的。调用开始先将标志量f设为false，f表示这次调用是否发现了一个环。把v放在栈stack中，然后将blocked数组的v设为true，即将此点阻塞。可以看到下方对于CIRCUIT的调用都是将s作为参数，所以stack的栈底一般都是s。下一步遍历Ak中第v个链表，即v出发的边指向的顶点。如果某个顶点与s相等，说明找到了一个环，这时执行输出环并把f设为true。否则如果这个顶点没有阻塞，说明还可以向下走，就递归调用此过程。

如果能够在v的邻接顶点中找到一条环路，则f就是true的，这时可以把v解锁，即调用unblock过程。反之，则说明从包含从v出发的边的路径都是死路，是不可能的形成环的，所以不能解锁v，同时要把与v邻接的顶点置于B数组的第v个链表中，经过v的路径是死路，但经过v的邻接顶点w的不一定死路，应为w可能有另外的上级顶点，所以如果不搜索v了，即解锁v顶点是要把B[v]中记录的顶点也解锁，以供其他路径搜索使用。

对v的调用结束时把v出栈。返回f，标志在这次调用中是否发现环。

下面是如何执行主进程。主进程涉及到寻找强连通分量(scc)，这部分可以参考tarjan算法。算法首先清空储存路径节点的栈，将搜寻起点s设为1，注意所有顶点编号从1开始。Ak初始化为在{s, s+1, s+2,...,n}这些顶点构成的子图里面所有强连通分量中，有最小顶点的分量的邻接表。Ak如果为空，说明图已经搜索完，算法结束。否则将s设为上述分量Ak里面最小的顶点，将blocked全置为false，B清空，以s为输入参数调用CIRCUIT。注意此时CIRCUIT只寻找以s开头的环路。调用完成将s加一，再在新的子图中寻找。

实例解析

下面是对上述过程的一个实例，来自YouTube一位Tushar Roy的视频主的教程（此君在YouTube上多有图论方面教程，可以学习，这个算法的视频我搬运到了B站，供诸君参考）。

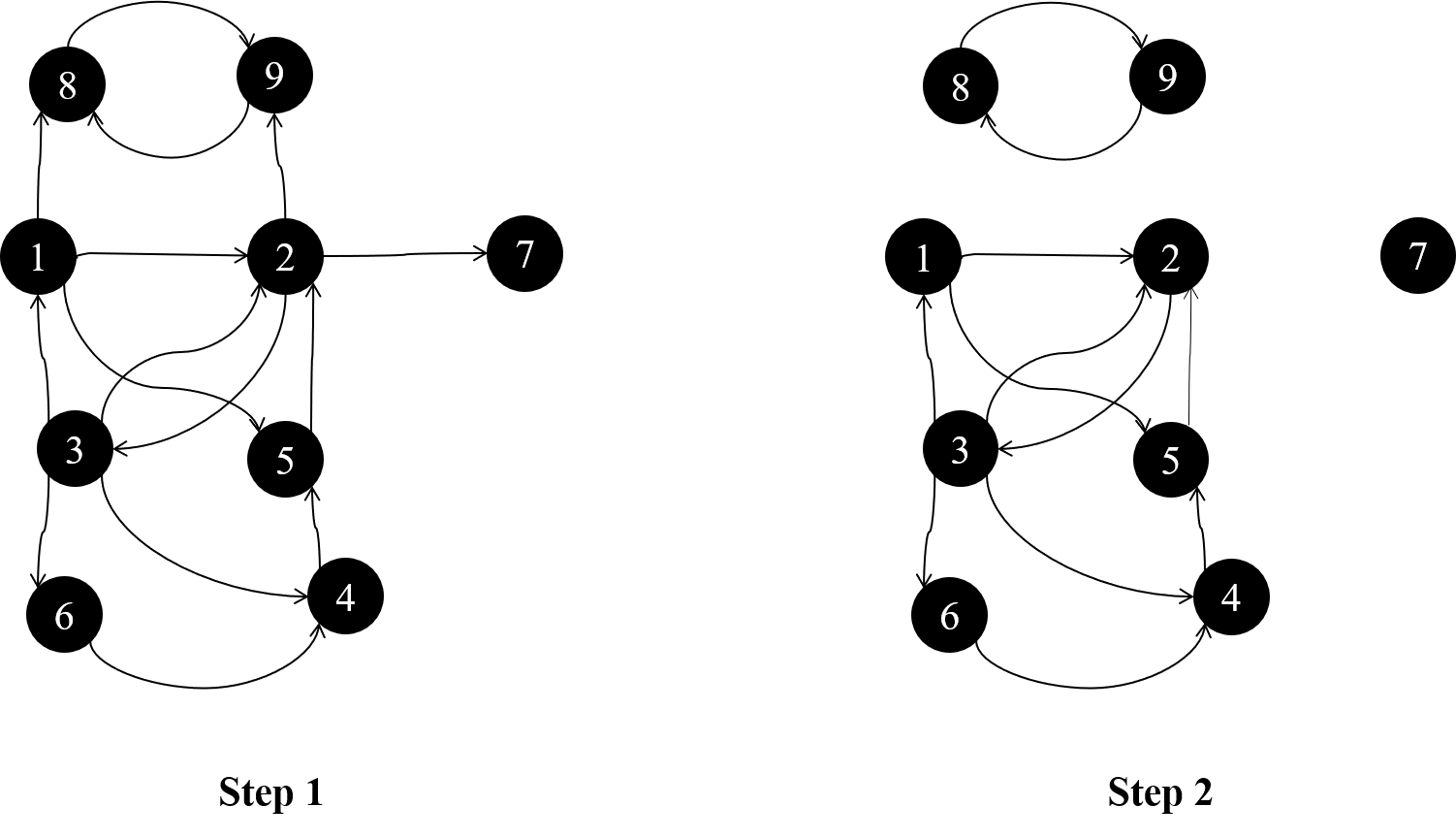
step1&2

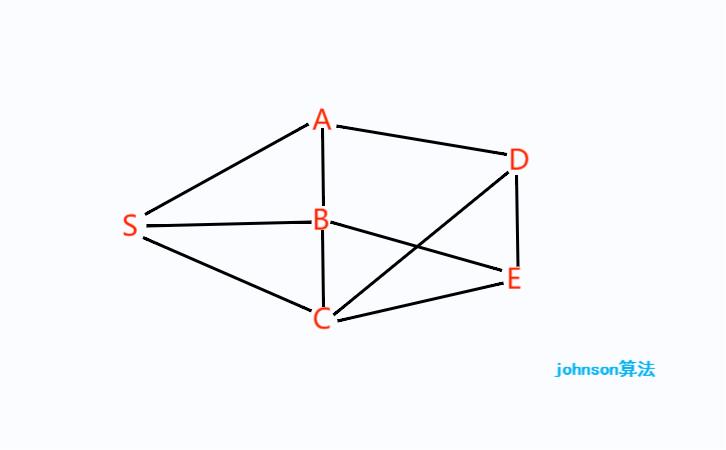
Step1是一个有向图G，Step2表示分解后的三个强连通分量，所谓强连通分量，就是在一个有向图中，任选两个顶点都可以互相到达。分解scc的tarjan算法在此不再赘述。

step3

发现1是最小的顶点，选取1所在的scc开始搜索，第一个调用顶点是1。step3-5是从1开始的3条遍历路径。上图所示，红色边表示搜索的路径，从1开始依次搜索1，2，3，到3的时候，栈里存储了这三个节点，并且blocked数组将这三个元素设为true。3有3个邻接顶点。首先搜索1，发现1是出发的顶点，表明找到了一个环，就将环输出，并把3这里调用的变量f设为true。

step4

回到顶点3后搜索下一个邻接顶点4，4没有阻塞说明还没有探索过，4只有一个邻接点5，走到5之后已经无路可走，因为5的唯一邻接顶点2处于blocked状态，所以以f为false返回这次调用，表明没有找到环。调用从2返回到5的时候看到返回值是false，这时把5放到B[2]的链表中。这种做法相当于告诉2节点：兄弟你解锁的时候把我也解锁了，你不解锁我也堵着算了，反正下次再找到我的时候，我的下家都是死路，找也是白找。所以，只有在调用UNBLOCK(2)的时候5才能解锁，这时blocked[5]还是保持blocked状态。返回的4的时候也是如此。需要把4保持阻塞，并把4放到B[5]的链表中。这时调用返回到了3节点。

step5

检索3的下一个邻居6，发现6的下家4还是阻塞的，于是这次调用也以失败返回。返回到3，3的邻居已经检索完，发现了一个环，所以f是true的，把3的阻塞解除，调用返回到2。因为3找到了一个环所以2的f也是true的，所以调用UNBLOCK(2)，这个过程把blocked[2]设为false之后，检索B[2]发现里面有一个元素5，因此递归调用把5也解锁了。依次调用，B就被清空了。

这就是一次1->2这个边开头的检索的完整过程。

本人水平有限，解读如果有失误之处欢迎交流。