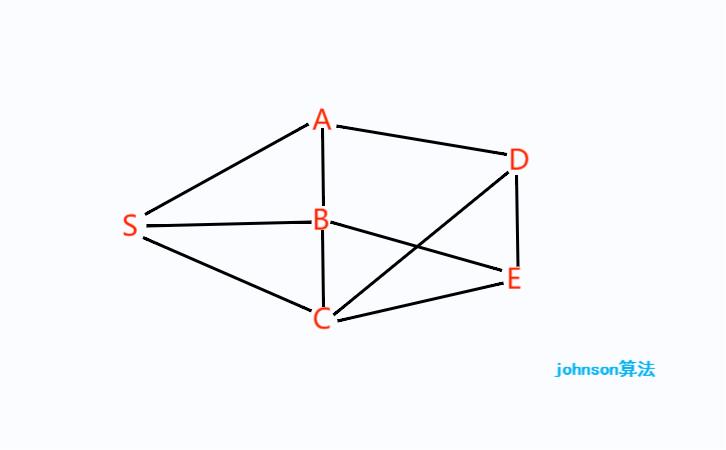
一、最短路径问题
问题是找到给定加权有向图中每对顶点之间的最短路径,权重可能为负。我们已经讨论了这个问题的Floyd-Warshall算法。Floyd-Warshall算法的时间复杂度为Θ(V3)。利用Johnson算法,我们可以在O(V2log V+VE)时间内找到所有对的最短路径。Johnson的算法使用Dijkstra和Bellman Ford作为子程序。如果我们对每个顶点应用Dijkstra的单源最短路径算法,将每个顶点作为源,我们可以在O(V*VLogV)时间内找到所有对最短路径。因此,使用Dijkstra的单源最短路径似乎比Floyd Warshall的算法更好(https://www.geeksforgeeks.org/floyd-warshall-algorithm-dp-16/?ref=lbp),但Dijkstra算法的问题是,它不适用于负权重边。Johnson算法的思想是重新加权所有边并使它们都为正,然后对每个顶点应用Dijkstra算法。如何将给定的图转换为具有所有非负权重边的图?可以考虑一种简单的方法,找到最小权重边并将此权重添加到所有边。不幸的是,这不起作用,因为在不同的路径中可能有不同数量的边(请参见此示例)。如果从顶点u到v有多条路径,则所有路径都必须以相同的数量增加,以便最短路径在变换后的图中保持最短。Johnson算法的思想是为每个顶点分配一个权重。设指定给顶点u的权重为h[u]。我们使用顶点权重重新加权边。例如,对于权重为w(u,v)的边(u,v),新权重将变为w(u,v)+h[u]–h[v]。这种重新加权的好处在于,任意两个顶点之间的所有路径集都以相同的数量增加,所有负权重都变为非负权重。考虑两个顶点s和t之间的任何路径,每条路径的权重都会增加h[s]–h[t],并且从s到t的路径上所有顶点的h[]值都会相互抵消。我们如何计算h[]值?Bellman-Ford算法用于此目的。下面是完整的算法。新顶点将添加到图形中,并连接到所有现有顶点。从新顶点到所有现有顶点的最短距离值为h[]值。算法:1)将给定的图设为G。向图中添加一个新顶点s,将新顶点的边添加到G的所有顶点。将修改后的图设为G’。2) 以s为源在G’上运行Bellman-Ford算法。设Bellman Ford计算的距离为h[0],h[1]。。h【V-1】。如果我们发现一个负的权重周期,那么返回。请注意,新顶点s无法创建负权重循环,因为s没有边。所有边都来自s。3)重新加权原始图形的边。对于每条边(u,v),将新权重指定为“原始权重+h[u]–h[v]”。4) 删除添加的顶点s,并对每个顶点运行Dijkstra算法。转换如何确保非负权重边?以下属性对于h[]值始终为真,因为它们是最短距离。
h【v】<=h【u】+w(u,v)
该属性仅表示从s到v的最短距离必须小于或等于从s到u的最短距离加上边的权重(u,v)。新权重为w(u,v)+h[u]–h[v]。由于不等式“h[v]<=h[u]+w(u,v)”,新权重的值必须大于或等于零。示例:让我们考虑下图。Johnson 1我们添加一个源s,并将s的边添加到原始图的所有顶点。下图中s为4。Johnson2我们使用Bellman-Ford算法计算从4到所有其他顶点的最短距离。从4到0、1、2和3的最短距离分别为0、-5、-1和0,即h[]={0、-5、-1、0}。获得这些距离后,我们移除源顶点4,并使用以下公式重新加权边。w(u,v)=w(u,v)+h[u]–h[v]。Johnson 3由于所有权重现在都为正,我们可以对每个顶点运行Dijkstra最短路径算法作为源。

二、约翰逊算法
Johnson算法寻找加权有向图中所有顶点对之间的最短路径。它允许一些边权重为负数,但可能不存在负权重循环。它使用Bellman-Ford算法重新加权原始图,移除所有负权重。Dijkstra算法应用于重加权图,以计算所有顶点对之间的最短路径。
算法描述
使用Dijkstra算法,可以找到O(V2logV)中所有顶点对之间的最短路径。然而,Dijkstra不适用于负权重。为了避免这个问题,Johnson的算法使用了一种称为重新加权的技术。
重新加权是一个过程,通过该过程,每个边的权重都会发生变化,以满足两个特性-
对于图中的所有顶点对u、v,如果重新加权之前这些顶点之间存在最短路径,则它也必须是重新加权之后这些顶点之间的最短路径。
对于图中的所有边(u,v),它们必须具有非负权重(u,v)。
Johnson的算法使用Bellman Ford重新加权边缘。Bellman Ford还能够检测到原始图表中存在的负重量周期。
三、Johnson的算法源代码
using System;
using System.Text;
using System.Linq;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public class Neighbour
{
public int destination { get; set; } = 0;
public int weight { get; set; } = 0;
public Neighbour(int d, int w)
{
this.destination = d;
this.weight = w;
}
}
public class Graph_Johnson_Algorithm
{
public int vertices;
public List<List<Neighbour>> adjacencyList;
public Graph_Johnson_Algorithm()
{
}
public Graph_Johnson_Algorithm(int vertices, int[,] adjacencyMatrix)
{
this.vertices = vertices;
adjacencyList = new List<List<Neighbour>>(vertices);
for (int i = 0; i < vertices; i++)
{
adjacencyList.Add(new List<Neighbour>());
}
for (int i = 0; i < vertices; i++)
{
for (int j = 0; j < vertices; j++)
{
if (adjacencyMatrix[i, j] != 0)
{
addEdge(i, j, adjacencyMatrix[i, j]);
}
}
}
}
public void addEdge(int source, int destination, int weight)
{
adjacencyList[source].Add(new Neighbour(destination, weight));
}
public int[] dijkstra(int source)
{
bool[] isVisited = new bool[vertices];
int[] distance = new int[vertices];
for (int i = 0; i < distance.Length; i++)
{
distance[i] = Int32.MaxValue;
}
distance[0] = 0;
for (int vertex = 0; vertex < vertices; vertex++)
{
int minDistanceVertex = findMinDistanceVertex(distance, isVisited);
isVisited[minDistanceVertex] = true;
foreach (Neighbour neighbour in adjacencyList[minDistanceVertex])
{
int destination = neighbour.destination;
int weight = neighbour.weight;
if (!isVisited[destination] && distance[minDistanceVertex] + weight < distance[destination])
{
distance[destination] = distance[minDistanceVertex] + weight;
}
}
}
return distance;
}
public int findMinDistanceVertex(int[] distance, bool[] isVisited)
{
int minIndex = -1;
int minDistance = Int32.MaxValue;
for (int vertex = 0; vertex < vertices; vertex++)
{
if (!isVisited[vertex] && distance[vertex] <= minDistance)
{
minDistance = distance[vertex];
minIndex = vertex;
}
}
return minIndex;
}
public int[] bellmanford(int source)
{
int[] distance = new int[vertices];
for (int i = 0; i < distance.Length; i++)
{
distance[i] = Int32.MaxValue;
}
distance[0] = 0;
for (int i = 0; i < vertices - 1; i++)
{
for (int currentVertex = 0; currentVertex < vertices; currentVertex++)
{
foreach (Neighbour neighbour in adjacencyList[currentVertex])
{
if (distance[currentVertex] != Int32.MaxValue && distance[currentVertex] + neighbour.weight < distance[neighbour.destination])
{
distance[neighbour.destination] = distance[currentVertex] + neighbour.weight;
}
}
}
}
for (int currentVertex = 0; currentVertex < vertices; currentVertex++)
{
foreach (Neighbour neighbour in adjacencyList[currentVertex])
{
if (distance[currentVertex] != Int32.MaxValue && distance[currentVertex] + neighbour.weight < distance[neighbour.destination])
{
return null;
}
}
}
return distance;
}
public int[,] johnsons()
{
this.vertices++;
adjacencyList.Add(new List<Neighbour>());
for (int i = 0; i < vertices - 1; i++)
{
adjacencyList[vertices - 1].Add(new Neighbour(i, 0));
}
int[] h = bellmanford(vertices - 1);
if (h == null)
{
return null;
}
for (int u = 0; u < vertices; u++)
{
List<Neighbour> neighbours = adjacencyList[u];
foreach (Neighbour neighbour in neighbours)
{
int v = neighbour.destination;
int w = neighbour.weight;
neighbour.weight = w + h[u] - h[v];
}
}
adjacencyList.RemoveRange(adjacencyList.Count - vertices - 1, vertices);
vertices--;
int[,] distances = new int[vertices, vertices];
for (int s = 0; s < vertices; s++)
{
int[] da = dijkstra(s);
for (int i = 0; i < da.Length; i++)
{
distances[s, i] = da[i];
}
}
for (int u = 0; u < vertices; u++)
{
for (int v = 0; v < vertices; v++)
{
if (distances[u, v] == Int32.MaxValue)
{
continue;
}
distances[u, v] += (h[v] - h[u]);
}
}
return distances;
}
}
public static partial class GraphDrives
{
public static string Jhonsons()
{
int vertices = 4;
int[,] matrix = {
{ 0, 0, -2, 0 },
{ 4, 0, 3, 0 },
{ 0, 0, 0, 2 },
{ 0, -1, 0, 0 }
};
Graph_Johnson_Algorithm graph = new Graph_Johnson_Algorithm(vertices, matrix);
int[,] distances = graph.johnsons();
if (distances == null)
{
return ("Negative weight cycle detected.");
}
return Algorithm_Gallery.ToHtml(distances);
}
}
}