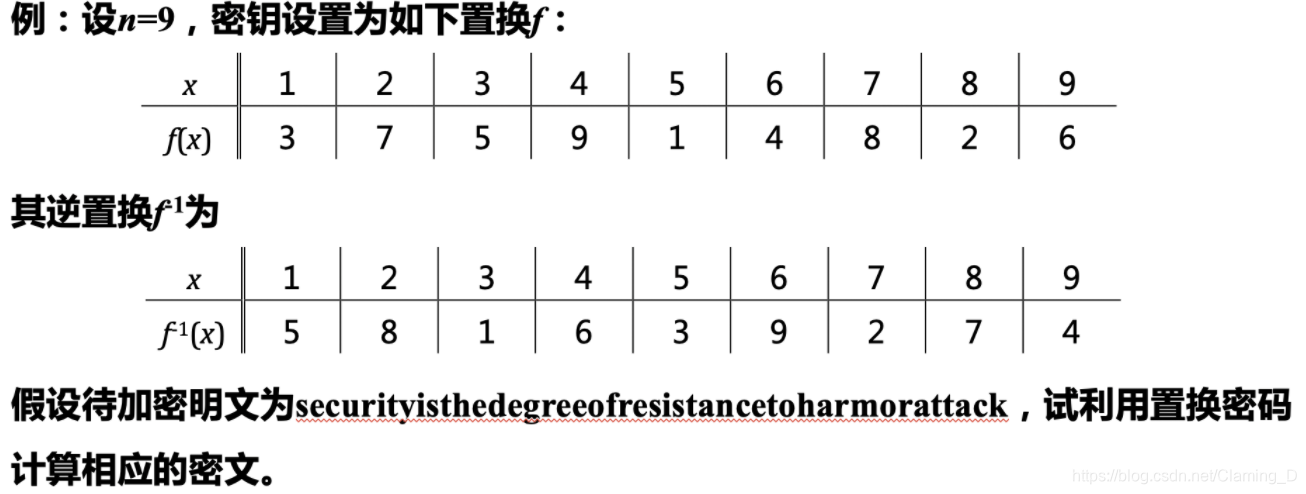
文章目录
- 2.1 代替技术
- 2.1.1 仿射密码
- 2.1.2 单表代替密码
- 2.1.3 Hill密码
- Hill密码的已知明文攻击
- 2.1.4 Vigenere密码
- 2.2 置换技术
- 2.2.1 栅栏密码
- 2.2.2 矩阵密码
作为较为朴素的密码体系,古典密码通常都是对称的。如下图所示,对称密码通常是加密方与解密方共享
相同密钥,通过
加密算法和
解密算法来进行秘密消息的传输。

在古典密码中,加密算法的核心是代替技术和置换技术。基于这两种技术诞生了多种多样的古典密码算法。虽然这些算法在如今的计算机体系之下已经不安全,但是它们蕴含的思想还是值得现在密码算法设计的借鉴。
2.1 代替技术
2.1.1 仿射密码
在密码技术诞生指出,人们想到最朴素的加密方式就是对明文进行简单的代数变换——线性同余变换。线性同余变换的表达式如(1)式所示。
y = a x + b ( m o d p ) (1) y = ax + b \pmod {p} \tag{1} y=ax+b(modp)(1)
仿射变换就是对一个向量空间进行 y = a x + b y =ax + b y=ax+b 的平移变换。(1)在仿射变换的基础上引入同余是为了便于密码的设计,当 p = 26 p = 26 p=26 时,可以在字母空间当中实现映射,实现如(2)式所示的加密和解密运算。
{ C = E n c a , b ( M ) = a M + b ( m o d 26 ) M = D e c a , b ( C ) = a − 1 ( C − b ) ( m o d 26 ) (2) \begin{cases} C = Enc_{a, b}(M) = aM + b \pmod {26} \\ M = Dec_{a, b}(C) = a^{-1}(C - b) \pmod {26} \end{cases} \tag{2} {C=Enca,b(M)=aM+b(mod26)M=Deca,b(C)=a−1(C−b)(mod26)(2)
注意到仿射密码中的乘数 a a a 和模数 p p p 必须互素,否则无法求 a a a 模 p p p 的逆元,进而无法解密。这要求了对于 p = 26 p = 26 p=26 , 2 ∤ a , 13 ∤ a 2 \nmid {a}, 13 \nmid {a} 2∤a,13∤a 。因此, a a a 的取值集合为{1,3,5,7,9,11,15,17,19,21,23,25}, b b b 的取值集合为 Z 26 Z_{26} Z26 ,但是密钥组 ( a , b ) (a, b) (a,b) 不能取 ( 1 , 0 ) (1, 0) (1,0) ,因为此时密钥为平凡密钥,加密结果 C = M C = M C=M ,无法实现数据机密性的安全需求。所以密钥空间大小为 12 × 26 − 1 = 311 12 \times 26 - 1 = 311 12×26−1=311,特别的,当 a = 1 a = 1 a=1 时,该加密算法又可称作Caesar密码。
仿射密码加解密算法的主要代码如下所示:
#注:该代码只能处理无空格小写英文。
#测试样例:
#密钥:a = 3,b = 7
#明文:thisisatest
#密文:mcfjfjhmtjm#加密算法
def enc(a, b, s):if a % 2 == 0 or a % 13 == 0:print('invalid key')returnfor p in s:p = ord(p) - ord('a')print(chr((a * p + b) % 26 + ord('a')), end='')
#解密算法
def dec(a, b, s):if a % 2 == 0 or a % 13 == 0:print('invalid key')returnfor c in s:c = ord(c) - ord('a')print(chr(((c - b) * euc_div(a, 26)[0]) % 26 + ord('a')), end='')
2.1.2 单表代替密码
由2.1.1的分析可知,仿射密码的密钥空间中只有311中组合,穷举法即可快速爆破。为了增强加密算法的安全性,古典密码的设计者们尝试增大密钥空间的大小,进而增加穷举攻击的难度,于是诞生了单表代替密码。
单表代替密码取一定的无重复字母序列作为密钥,可通过密钥助记字来构造密钥。将密钥序列补全未出现的字母,作为明文序列;同时将顺序的26个字母作为密文序列与明文序列一一对应,可以构造明密文对照表。由于加密方式是26个明文字母和密文字母的一一映射,所以单表代替密码的密钥空间为 26 ! 26! 26!,其安全性大大增加。举个例子:
1. 设明文为:basilisk to leviathan blake is contact
2. 密钥助记字为:The snow lay thick on the steps and the snowflakes driven by the wind looked black in the headlights of the cars
3. 提取出所有不重复的字母:thesnowlayickpdfrvbg
4.构造明密文对照表:
| 明文字母 | t | h | e | s | n | o | w | l | a | y | i | c | k |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 密文字母 | a | b | c | d | e | f | g | h | i | j | k | l | m |
| 明文字母 | p | d | f | r | v | b | g | j | m | q | u | x | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 密文字母 | n | o | p | q | r | s | t | u | v | w | x | y | z |
5. 得到密文:sidkhkdm af hcrkiabie shimc kd lfeaila
注:解密时明密文对照表不变
单表代替密码加解密算法的主要代码如下所示:
#注:该代码只支持无空格小写英文信息。
#测试样例:
#密钥助记字:thesnowlaythickonthestepsandthesnowflakesdrivenbythewindlookedblackintheheadlightsofthecars
#明文:basilisktoleviathanblakeiscontact
#密文:sidkhkdmafhcrkiabieshimckdlfeaila#获取明密文对照表
def get_table(sentense: str):res, alb = {}, ord('a')for char in sentense:if char == ' ': continueif char not in res:res[char] = chr(alb)alb += 1for i in range(26):if chr(i + ord('a')) not in res:res[chr(i + ord('a'))] = chr(alb)alb += 1return res#加密算法
def enc(s, k: dict):ans = ''for char in s:if char == ' ': continueans += k[char]return ans
#解密算法
def dec(s, k: dict):m, c, ans = k.keys(), k.values(), ''new_key = dict(zip(c, m))for char in s:if char == ' ': continueans += new_key[char]return ans
2.1.3 Hill密码
尽管单表代替密码的密钥空间已经大于DES的密钥空间( 26 ! > 4 × 1 0 26 26! > 4 \times {10 ^ {26}} 26!>4×1026),抗穷举攻击能力较强,但是它的安全性仍然较弱。这是因为明文中的每一个元素仅对密文中的一个元素产生影响,导致单表代替密码的密文仍含有明文的一阶语言特征,即明文的字母频率仍体现在密文当中。因此在密文样本量足够大时,可以用《福尔摩斯探案集》中“跳舞的小人”故事里那样,通过分析密文字母的出现频率来判断密文字母所对应的明文字母。
为了掩盖单表代替密码中密文的字母统计规律,人们提出多种多字母代替密码,其中最为典型的一种为Hill密码。Hill密码为乘法密码的扩展(即密文为明文与一个数相乘的结果),但在Hill密码中,密文由m个方程与明文相乘的结果组成,这m个方程可以表示为一个m维密钥矩阵 K \boldsymbol{K} K,则密文可以表示为密钥矩阵模26条件下左乘或右乘明文矩阵,由此可以得到如(3)式所示的加解密过程:
{ C = E n c K ( M ) = M K ≡ K T M ( m o d 26 ) M = D e c K ( C ) = C K − 1 ≡ ( K T ) − 1 C ( m o d 26 ) (3) \begin{cases} \boldsymbol{C} = Enc_{\boldsymbol{K}}(\boldsymbol{M}) = \boldsymbol{M}\boldsymbol{K} \equiv \boldsymbol{K}^T\boldsymbol{M} \pmod{26} \\ \boldsymbol{M} = Dec_{\boldsymbol{K}}( \boldsymbol{C}) = \boldsymbol{C}\boldsymbol{K} ^ {-1} \equiv (\boldsymbol{K} ^ T) ^ {-1} \boldsymbol{C} \pmod {26} \end{cases} \tag{3} {C=EncK(M)=MK≡KTM(mod26)M=DecK(C)=CK−1≡(KT)−1C(mod26)(3)
注: K − 1 = 1 ∣ K ∣ K ∗ \boldsymbol{K} ^ {-1} = \frac{1}{|\boldsymbol{K}|}\boldsymbol{K} ^ * K−1=∣K∣1K∗
Hill密码加解密算法的主要代码如下所示:
import copy
#注:该代码只支持无空格小写英文信息。n为密钥矩阵维数,K为密钥矩阵。尽管numpy库中以包含矩阵运算,但是Hill密码中的矩阵乘法和求逆均需要模26,因此给出其源码。
#测试样例:
#n = 2
#K= [[9, 5], [4, 7]]
#明文:meetmeatcsdn
#密文:ukixukydmgbc
def matrixMul(A, B):if len(A[0]) == len(B):res = [[0] * len(B[0]) for i in range(len(A))]for i in range(len(A)):for j in range(len(B[0])):for k in range(len(B)):res[i][j] += A[i][k] * B[k][j]res[i][j] %= 26return resdef submatrix(A, i, j):# 矩阵A第i行第j列元素的余矩阵p = len(A) # 矩阵的行数q = len(A[0]) # 矩阵的列数C = [[A[x][y] for y in range(q) if y != j] for x in range(p) if x != i] # 列表推导式return C
def det(A):# 按第一行展开递归求矩阵的行列式p = len(A) # 矩阵的行数q = len(A[0]) # 矩阵的列数if (p == 1 and q == 1):return A[0][0]else:value = 0for j in range(q):value += ((-1) ** (j + 2)) * A[0][j] * det(submatrix(A, 0, j))return value
def matrixInverse(A):p = len(A) # 矩阵的行数q = len(A[0]) # 矩阵的列数C = copy.deepcopy(A)d = det(A)# print(d)for i in range(p):for j in range(q):C[i][j] = ((-1) ** (i + j + 2)) * det(submatrix(A, j, i))C[i][j] = (C[i][j] * euc_div(d, 26)[0]) % 26return C#加密算法
def enc(n, K, s):for i in range(0, len(s), n):tmp_P = []for j in range(n):tmp_P.append(ord(s[i + j]) - ord('a'))tmp_P = [tmp_P]tmp_C = matrixMul(tmp_P, K)for j in range(n):print(chr(tmp_C[0][j] + ord('a')), end='')
#解密算法
def dec(n, K, s):K = matrixInverse(K)for i in range(0, len(s), n):tmp_P = []for j in range(n):tmp_P.append(ord(s[i + j]) - ord('a'))tmp_P = [tmp_P]tmp_C = matrixMul(tmp_P, K)for j in range(n):print(chr(tmp_C[0][j] + ord('a')), end='')
Hill密码的已知明文攻击
尽管Hill密码有足够的安全性抵抗唯密文攻击,但它不具备抵抗已知明文攻击的能力。Hill密码的已知明文攻击具体执行步骤如下所示:
1. 对于n为密钥矩阵 K \boldsymbol{K} K,获取n维可逆的明文
M = ( m 11 ⋯ m 1 n ⋮ ⋱ ⋮ m n 1 ⋯ m n n ) \boldsymbol{M} = \left( \begin{matrix} m_{11} & \cdots & m_{1n} \\ \vdots & \ddots & \vdots \\ m_{n1} & \cdots & m_{nn} \end{matrix} \right) M= m11⋮mn1⋯⋱⋯m1n⋮mnn 及其对应的n维可逆密文 C = ( c 11 ⋯ c 1 n ⋮ ⋱ ⋮ c n 1 ⋯ c n n ) \boldsymbol{C} = \left( \begin{matrix} c_{11} & \cdots & c_{1n} \\ \vdots & \ddots & \vdots \\ c_{n1} & \cdots & c_{nn} \end{matrix} \right) C= c11⋮cn1⋯⋱⋯c1n⋮cnn
2. 由加密运算 C = M K ( m o d 26 ) \boldsymbol{C} = \boldsymbol{M}\boldsymbol{K} \pmod {26} C=MK(mod26) 可知:
K = M − 1 C ≡ ( m 11 ⋯ m 1 n ⋮ ⋱ ⋮ m n 1 ⋯ m n n ) − 1 ( c 11 ⋯ c 1 n ⋮ ⋱ ⋮ c n 1 ⋯ c n n ) ( m o d 26 ) \boldsymbol{K} = \boldsymbol{M} ^ {-1} \boldsymbol{C} \equiv \left( \begin{matrix} m_{11} & \cdots & m_{1n} \\ \vdots & \ddots & \vdots \\ m_{n1} & \cdots & m_{nn} \end{matrix} \right) ^ {-1} \left( \begin{matrix} c_{11} & \cdots & c_{1n} \\ \vdots & \ddots & \vdots \\ c_{n1} & \cdots & c_{nn} \end{matrix} \right) \pmod {26} K=M−1C≡ m11⋮mn1⋯⋱⋯m1n⋮mnn −1 c11⋮cn1⋯⋱⋯c1n⋮cnn (mod26)
由此得到密钥矩阵 K \boldsymbol{K} K,攻击成功!
上述过程的代码如下所示:
#注:n为密钥矩阵的维数
#测试样例:
#明文:thisistestfortheknownplaintextattack
#密文:wvlomkzsbyjjwdisydygrqtfrpnfxnhthysu
#n = 3
#密钥矩阵:[[7, 2, 15], [25, 25, 6 ], [0, 2, 19 ]]
def attack(msg, cript, n):p_m, c_m = [[] for _ in range(n)], [[] for _ in range(n)]len_list = len(msg)for i in range(0, len_list - n * n, n):p_m, c_m = [[] for _ in range(n)], [[] for _ in range(n)]p = list(msg[i:n * n + i])c = list(cript[i:n * n + i])for j in range(n):for k in range(n):p_m[j].append(ord(p[j * n + k]) - ord('a'))c_m[j].append(ord(c[j * n + k]) - ord('a'))if euc_div(det(p_m), 26)[2] == 1 & euc_div(det(c_m), 26)[2] == 1:break# print(p_m, c_m)key = matrixMul(matrixInverse(p_m), c_m)for i in range(len(key)):for j in range(len(key[0])):print(key[i][j], end=' ')print()
2.1.4 Vigenere密码
尽管以Hill密码为代表的多字母代替密码能够掩盖明文部分统计信息,但是在一定条件下仍然会暴露明文的多字母结构,因此研究如何能够完全掩盖明文的字母信息显得十分重要。
为了进一步提升代替密码的安全性,人们发明了多表代替的Vigenere密码。设明文字母序列为 M = m 1 m 2 ⋯ m p M = m_1m_2 \cdots m_p M=m1m2⋯mp、密钥序列为 K = k 1 k 2 ⋯ k q K = k_1k_2 \cdots k_q K=k1k2⋯kq、密文序列 C = c 1 c 2 ⋯ c p C = c_1c_2 \cdots c_p C=c1c2⋯cp,则Vigenere密码的加解密过程可以表示为(4)式:
{ c i = E n c k i = m i + k i ( m o d q ) ( m o d 26 ) , i = 1 , 2 , ⋯ , p m i = D e c k i = c i − k i ( m o d q ) ( m o d 26 ) , i = 1 , 2 , ⋯ , p (4) \begin{cases} c_i = Enc_{k_i} = m_i + k_{i \pmod {q}} \pmod {26}, \quad i = 1, 2, \cdots, p \\ m_i = Dec_{k_i} = c_i - k_{i \pmod {q}} \pmod {26}, \quad i = 1, 2, \cdots, p \end{cases} \tag{4} {ci=Encki=mi+ki(modq)(mod26),i=1,2,⋯,pmi=Decki=ci−ki(modq)(mod26),i=1,2,⋯,p(4)
由上式可以观察到,密钥序列的长度可以小于明文或密文序列,但当且仅当密钥序列与明密文序列长度一致时,加密的安全性最高。
Vigenere密码加解密算法的主要代码如下所示:
#测试样例:
#密钥:explanation
#明文:welcometocsdnformyblogs
#密文:abanozemwqfhkuzrzyutctw#加密算法
def enc(k, s):k_len = len(k)for i in range(len(s)):print(chr((ord(s[i]) + ord(k[i % k_len]) - 2 * ord('a')) % 26 + ord('a')), end='')
#解密算法
def dec(k, s):k_len = len(k)for i in range(len(s)):print(chr((ord(s[i]) - ord(k[i % k_len])) % 26 + ord('a')), end='')
2.2 置换技术
2.2.1 栅栏密码
栅栏密码的主要流程为将一行明文分组,每组含有密钥 k k k 个字母,得到消息矩阵,将消息矩阵逐列输出,得到密文。解密流程与加密流程相似,但是每组字母数量为 l ÷ k l \div k l÷k 个。栅栏密码加解密算法的主要代码如下所示:
#注:n为密钥长度
#测试样例:
#密钥:3
#明文:kirhauunomhiyduinaumhzntoinoemoihouenosbous
#密文:khumyiuzoooonbsianhdnmnieiuooruoiuahtnmhesu#加密算法
def enc(k, s):groups = [''] * kfor i in range(len(s)):groups[i % k] += s[i]for string in groups:print(string, end='')#解密算法
def dec(k, s):n_q = len(s) // kn_r = len(s) % ks = list(s)groups = [''] * kfor i in range(n_r):for j in range(n_q + 1):groups[i] += s.pop(0)for i in range(n_r, k):for j in range(n_q):groups[i] += s.pop(0)groups[i] += ' 'for i in range(len(groups[0])):for j in range(k):if groups[j][i] != ' ':print(groups[j][i], end='')
2.2.2 矩阵密码
矩阵密码的核心在于构造消息矩阵,并按照密钥规定的序列进行置换。举个例子:
加密过程:
1. 设明文为:attackpostponeduntiltwoamxyz;
2. 密钥为长度为7的序列:4312567;
3. 将明文逐列书写构造7行消息矩阵:
( a o d w t s u o t t n a a p t m c o i x k n l y p e t z ) \left( \begin{matrix} a & o & d & w \\ t & s & u & o \\ t & t & n & a \\ a & p & t & m \\ c & o & i & x \\ k & n & l & y \\ p & e & t & z \\ \end{matrix} \right) attackpostponeduntiltwoamxyz
4. 设矩阵行号与密钥序列对应,将矩阵置换回1234567的顺序:
( t t n a a p t m t s u o a o d w c o i x k n l y p e t z ) \left( \begin{matrix} t & t & n & a \\ a & p & t & m \\ t & s & u & o \\ a & o & d & w \\ c & o & i & x \\ k & n & l & y \\ p & e & t & z \\ \end{matrix} \right) tatackptpsoonentudiltamowxyz
5. 按行输出消息矩阵,得到密文:ttnaaptmtsuoaodwcoixknlypetz。
解密过程:
1. 设密文为:ttnaaptmtsuoaodwcoixknlypetz;
2. 密钥为长度为7的序列:4312567;
3. 将密文逐行书写构造7列消息矩阵:
( t t n a a p t m t s u o a o d w c o i x k n l y p e t z ) \left( \begin{matrix} t & t & n & a \\ a & p & t & m \\ t & s & u & o \\ a & o & d & w \\ c & o & i & x \\ k & n & l & y \\ p & e & t & z \\ \end{matrix} \right) tatackptpsoonentudiltamowxyz
4. 设矩阵行号顺序为1234567,将其按密钥序列的顺序置换:
( a o d w t s u o t t n a a p t m c o i x k n l y p e t z ) \left( \begin{matrix} a & o & d & w \\ t & s & u & o \\ t & t & n & a \\ a & p & t & m \\ c & o & i & x \\ k & n & l & y \\ p & e & t & z \ \end{matrix} \right) attackpostponeduntiltwoamxyz
5. 按列输出消息矩阵,得到明文:attackpostponeduntiltwoamxyz。
矩阵密码加解密算法的主要代码如下所示:
#注:n为密钥长度
#测试样例:
#n = 7
#密钥:4312567
#明文:attackpostponeduntiltwoamxyz
#密文:ttnaaptmtsuoaodwcoixknlypetz#加密算法
def enc(n, k, s):groups = [''] * nfor i in range(len(s)):groups[i % n] += s[i]for i in range(1, n + 1):pos = k.index(str(i))print(groups[pos], end='')
#解密算法
def dec(n, k, s):n_g = len(s) // ngroups = [''] * nfor i in range(len(s)):groups[i // n_g] += s[i]for i in range(n_g):for j in range(n):print(groups[int(k[j]) - 1][i], end='')