古典密码
- 凯撒密码
- 凯撒位移(中文版)
- 栅栏密码
- 棋盘密码
- 乘法密码
- 仿射密码
- 希尔密码
- 摩斯电码
- 猪圈密码
- 键盘密码
- 参考
凯撒密码
加密公式:密文 = (明文 + 位移数) Mod 26
解密公式:明文 = (密文 - 位移数) Mod 26

凯撒位移(中文版)
就是按照中文字在Unicode编码表中的顺序进行移位,可以用来加密中文的信息。
例:[中文凯撒移位]
转换成Unicode编码:中文凯撒移位
移1位后成为: 丮斈凰撓秼低
转换成中文:[丮斈凰挠秼低]
https://blog.csdn.net/qq_36134761/article/details/80385862
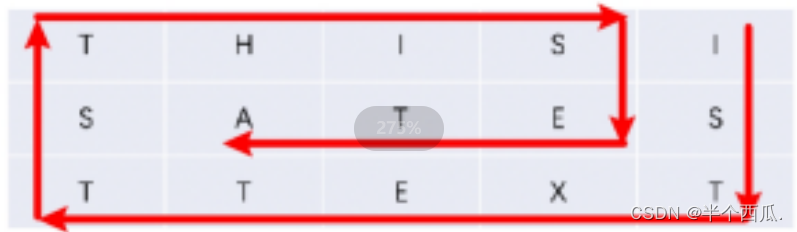
栅栏密码
也称栅栏易位(Columnar Transposition),即把将要传递的信息中的字母交替排成上下两行,再将下面一行字母排在上面一行的后边,从而形成一段密码。栅栏密码是一种置换密码。
例如密文:TEOGSDYUTAENNHLNETAMSHVAED
解密过程:先将密文分为两行
T E O G S D Y U T A E N N
H L N E T A M S H V A E D
再按上下上下的顺序组合成一句话
THE LONGEST DAY MUST HAVE AN END.
加密时不一定非用两栏,还是举《数字城堡》中的一个例子,密文为:
PFEE SESN RETM MFHA IRWE OOIG MEEN NRMA ENET SHAS DCNS IIAA IEER BRNK FBLE LODI
去掉空格:PFEESESNRETMMFHAIRWEOOIGMEENNRMAENETSHASDCNSIIAAIEERBRNKFBLELODI
共64个字符,以8个字符为一栏,排列成8*8的方阵(凯撒方阵):
P F E E S E S N
R E T M M F H A
I R W E O O I G
M E E N N R M A
E N E T S H A S
D C N S I I A A
I E E R B R N K
F B L E L O D I
从上向下竖着读:PRIMEDIFFERENCEBETWEENELEMENTSRESMONSIBLEFORHIROSHIMAANDNAGASAKI
插入空格:PRIME DIFFERENCE BETWEEN ELEMENTS RESMONSIBLE FOR HIROSHIMA AND NAGASAKI (广岛和长崎的原子弹轰炸的最主要区别)
棋盘密码
假设我们需要发送明文讯息 “Attack at once”, 用一套秘密混杂的字母表填满波利比奥斯方阵,像是这样:
1 2 3 4 5
1 b t a l p
2 d h o z k
3 q f v s n
4 g j c u x
5 m r e w y
i和j视为同一个字,使字母数量符合 5 × 5 格。之所以选择这五个字母,是因为它们译成摩斯密码时不容易混淆,
可以降低传输错误的机率。使用这个方格,找出明文字母在这个方格的位置,再以那个字母所在的栏名称和列名称代替这个字母。
可将该讯息转换成处理过的分解形式。
明文:A T T A C K A T O N C E
密文:AF AD AD AF GF DX AF AD DF FX GF XF
13 12 12 13 43 25 13 12 23 35 43 53
棋盘密码(ADFGX加密法),也就是所谓的坐标加密法,早在公元2世纪就被希腊人发明出来了,是密码史上第一个密码,值得我们去了解。


乘法密码
乘法密码也是一种简单的替代密码,与凯撒密码相似,凯撒密码用的是加法,而乘法密码用的自然是乘法。
这种方法形成的加密信息保密性比较低。
加密公式:密文 = (明文 * 乘数) Mod 26
对于乘数密码,只有当乘数与26互质时,加密之后才会有唯一的解,因此乘数只可能有如下11种的选择:
乘数 = 3,5,7,9,11,15,17,19,21,23,25
仿射密码和希尔密码因为都用到了乘法,所以乘数也受到相同的局限。
仿射密码
仿射密码就是凯撒密码和乘法密码的结合。
加密公式:密文 = (明文 * 乘数 + 位移数) Mod 26
希尔密码
希尔密码(Hill Cipher)是运用基本矩阵论原理的替换密码,由Lester S. Hill在1929年发明。每个字母当作26进制数字:A=0, B=1, C=2… 一串字母当成n维向量,跟一个n×n的矩阵相乘,再将得出的结MOD26。
考虑讯息ACT,因为A=0,C=2,T=19,讯息是:
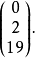
设密匙为
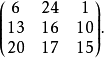
确认它是可逆的:
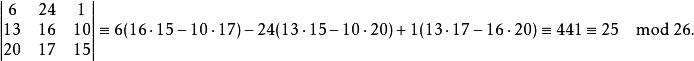
加密过程:
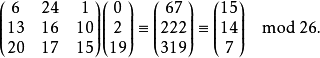
对应的密文便是“POH”。
假设对方知道密文和密匙,首先找出密匙的逆矩阵:

将逆矩阵和密文相乘:

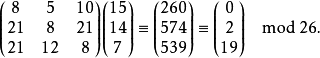
便得到“ACT”。
摩斯电码
摩斯电码(摩尔斯电码)是一种发报用的信号代码,是一种替代密码,用点(Dot)和划(Dash)的组合来表示各个英文字母或标点。

猪圈密码
猪圈密码(亦称朱高密码、共济会暗号、共济会密码或共济会员密码),是一种以格子为基础的简单替代式密码。即使使用符号,也不会影响密码分析,亦可用在其它替代式的方法。

键盘密码
加密的原理同棋盘密码,只是利用了键盘作为方阵。
键盘的字母分布:
~ ! @ # $ % ^ & * ( ) _ + |
` 1 2 3 4 5 6 7 8 9 0 - = \
Q W E R T Y U I O P { }
q w e r t y u i o p [ ]
A S D F G H J K L : "
a s d f g h j k l ; ’
Z X C V B N M < > ?
z x c v b n m , . /
密文:72 81 12 63 01 12 63
明文:jianpan
低下头看看键盘就知道了,密文就是键盘上的26个字母的坐标,72即第7列第2行,第7列正好是数字键[7]的位置,往下2个就是字母[J]。
参考
https://blog.csdn.net/qq_34206560/article/details/83242664
https://www.cnblogs.com/gwind/p/7997922.html