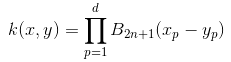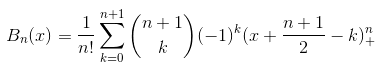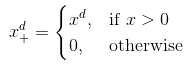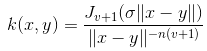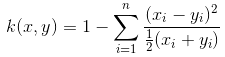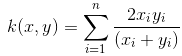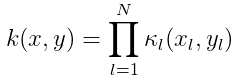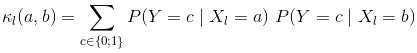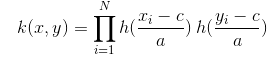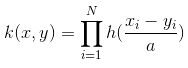核函数(Kernel function)(举例说明，通俗易懂)

已知有一组向量，可用线性函数去探索其是否具有线性关系，若数据之间是非线性呢？

非线性数据是指只有利用非线性模型才能更好的预测。但非线性问题往往不好求解，所以希望用解线性分类问题的方法解决这个问题。所采取的方法是进行一个非线性变换，将非线性问题变换为线性问题，通过解变换后的线性问题的方法求解原来的非线性问题。原理是将数据映射到高维数据，在高维空间线性可分。如下图，从低维转换到高维， $\Phi$ 是转换函数。

但是有个问题，高维空间的数据计算存在困难。所以替代方案是在特征空间中计算相似度度量，而不是计算向量的坐标，然后应用只需要该度量值的算法。用点积(dot product)表示相似性度量。

1、核函数定义

将原始空间中的向量作为输入向量，并返回特征空间（转换后的数据空间,可能是高维）中向量的点积的函数称为核函数。

使用内核，不需要显式地将数据嵌入到空间中，因为许多算法只需要图像向量之间的内积（内积是标量）；在特征空间不需要数据的坐标。

例1：考虑一个带有特征映射的二维输入空间 $\chi \subseteq \mathbb{R}^2$ ：

特征映射二维到三维： $\Phi:x=(x_1,x_2)\rightarrow \Phi(x)=(x_1^2,x_2^2,\sqrt{2}x_1x_2)\in F=\mathbb{R}^3$

特征空间中的内积： $\left \langle \Phi(x),\Phi(z) \right \rangle =\left \langle (x_1^2,x_2^2,\sqrt{2}x_1x_2),(z_1^2,z_2^2,\sqrt{2}z_1z_2) \right \rangle$

$=x_1^2z_1^2+x_2^2z_2^2+2x_1x_2z_1z_2$

$=\left \langle x_1z_1+x_2z_2 \right \rangle^2$

$=\left \langle x,z\right \rangle^2$

根据上面得，核函数为 $k(x,z)=\left \langle x,z \right \rangle^2= \Phi(x)^T\Phi(z)$

但核函数只是计算映射的内积，所以映射为 $\Phi(x)=(x_1^2,x_2^2,x_1x_2,x_2x_1)\in F=\mathbb{R}^4$ 也是可以得到上面的核函数但是特征空间变为4维了，所以对核函数来说特征空间不唯一。

怎么理解高斯核可以扩展为无限维？拿上例来说， $k(x,z)=\left \langle x,z \right \rangle^2=x_1^2z_1^2+x_2^2z_2^2+2x_1x_2z_1z_2$ 可以扩展为 $\Phi(x)=(x_1^2,x_2^2,\sqrt{2}x_1x_2)$ 和 $\Phi(x)=(x_1^2,x_2^2,x_1x_2,x_2x_1)$ 或者其他，只要最后两个向量的点积是核函数的形式即可，对于高斯核函数则可以扩展到无限维。

对于核函数一般有以下两个属性（不是所有的核函数）：

对称性（symmetric） $\forall x,z\in \chi ,k(x,z)=k(z,x)$

非负性（non-negative） $\forall x,z\in \chi ,k(x,z)\geq 0$

补充：输入空间一般是欧式空间或离散集合；输出空间也叫希尔伯特空间 $H$ ，是一个具有自然内积或点积的向量空间。

2、Mercer核

设 $X=\left \{ x_1,...,x_n \right \}$ 是一个有限集合来自输入空间 $\chi$ 。 $\chi$ 空间的格拉姆矩阵（Gram matrix）被定义为 $K(X;k)\in R^{n\times n}$ 或

$(K)_{ij} = k(x_i,x_j)$ 。

若对 $\forall X\subseteq \chi$ ，矩阵 $K$ 是正定的， $k$ 叫做Mercer核或叫正定核(positive definite：pd)。Mercer核是对称的即 $K=K^T$

Mercer's theorem:如果Gram矩阵是正定的，则可以计算Gram 矩阵的特征向量进行降维：

$K=U^T\Lambda U$

$\Lambda=diag(\lambda_1,...,\lambda_n)$ ， $\lambda_i$ 是 $K$ 的第 i 个特征值，因为矩阵是正定的所以 $\lambda_i> 0$ 。

$K$ 中的每个元素都是两个向量的点积，可以写成：

$K_{ij}=\phi(x_i)^T\phi(x_j)$

内核的每个元素都可以描述为一个函数 $\phi(\cdot )$ 应用到对象 $x_i,x_j$ 的内积。Mercer核的每个元素都位于Hilbert空间中，Hilbert空间是由两个任意向量的内积定义的抽象向量空间。

$\phi(\cdot )$ 被称为基函数（basis function），空间 F 描述为特征空间，即使用基函数将对象映射到特征空间 F。

基函数 $\phi(\cdot )$ (Mercer内核)可以写成κ的特征函数的线性组合。特征空间 F 的维数绝对没有限制;事实上，F可能是无限维的。注意以下两点：

许多内核方法不需要明确计算 $\phi(x )$ ，只需要使用内核函数 $k(\cdot ,\cdot )$ 计算 $n\times n$ 的Gram 矩阵。换句话说，可以在任意复杂的F特征空间中构建分类器，但不需要显式地计算该空间中的任何元素。
计算 $\phi(x )$ 很难(通常是不必要的)，直接使用直观的基函数 $\phi(x )$ 来构建内核 $k(\cdot ,\cdot )$ 。

简单来说就是应用核技巧：

将数据映射到高维空间，然后用点积比较这些数据
避免在高维空间运作，选择一个特征空间，其中点积可以使用输入空间中的非线性函数直接求值

例2：假设在一维空间中有n个点（均为标量），如何利用核函数将其转到高维空间进行分类？

对于一维空间的点 $x_i$ （代表一个样本）可以将其转换为向量 $(x_i,x_i^2)$ ，即 $\phi(x_i )=(x_i,x_i^2)$ 。根据核函数的定义可得：

$k(x_i,x_j)=\left \langle (x_i,x_i^2),(x_j,x_j^2) \right \rangle$

$=x_ix_j+x_i^2x_j^2$

上例中通过将转换函数 $\phi(x )$ ，将一维空间的变量转换到二维空间，计算简单，如上图所示，在特征空间线性可分。上式也可以尝试转换到更高维。

核函数方法的主要思想是活得一组观测数据，并将它们投影到另一空间，在这个空间中，点之间的比较是直接的。特征空间的位数可以是任意维，但可以在这个复杂的特征空间中使用简单的分类器，但要注意过拟合（特征过多会引起过拟合）。

3 构建核函数

3.1 线性核函数

让转换函数 $\phi(x )=x$ ，则得到线性核函数，则两个向量的点积为：

$k(x,{x}')=x^T{x}'$

线性核函数的特征空间F的维度与输入控件 $\chi$ 的维度一样，每个向量的特征数也一样( $x=(x_1,x_2,....)$ , $x_1$ 叫特征， $x$ 代表一个样本）。

当不需要在特征空间进行运算时，可以用线性核函数。如原始数据已经是高维的、可比较的，并且在输入空间线性可分。

线性内核适用于由大量固定长度的特征表示的对象(例如字袋)。

注：一个向量代表一个样本，一个样本有多个特征

3.2 高斯核函数

高斯核也叫squared exponential kernel 、SE kernel or radial basis function （RBF），形式如下：

$k(x,x')=exp(-\frac{1}{2}(x-x')^T\Sigma ^{-1}(x-x'))$

$\Sigma$ 是观测中每个特征的协方差，p维矩阵。当 $\Sigma$ 是对角线矩阵时，可以写为：

$k(x,x')=exp(-\frac{1}{2}\sum_{j=1}^p\frac{(x_j-x'_j)^2}{\sigma _j^2})$

$\sigma_j$ 被定义为特征 $j$ 的伸缩尺度(characteristic length scale)。

如果 $\Sigma$ 是球形的，则有：

$k(x,x')=exp(-\frac{\left \| x-x' \right \|^2}{2\sigma^2}),\sigma_j=\sigma,\forall j$

该核函数的特征空间的维度是无限的。核函数避免了转换函数的计算，所以可以用相对马氏距离计算 $n\times n$ 的Gram 矩阵

，即使已经隐式地将对象投射到无限维的特征空间中。

3.3 核函数类别

核函数类别(x,y表示输入空间的向量)

名称	表达式	参数
linear kernel	$k(x,y)=x^Ty+c$	c:常数
polynomial kernel	$k(x,y)=(\alpha x^Ty+c)^d$	alpha:slope c:constant;c=0,同质多项核函数;c=1,不同质多项核函数 d≥1，多项式次数
gaussian kernel	$k(x,y)=exp(- \frac{\|\|x-y\|\|^2}{2\sigma^2})=exp(-\gamma \|\|x-y\|\|^2)$
radial kernel	$k(x,y)=exp(-\gamma \|\|x-y\|\|^2)$	正常 $\gamma$ = 1/n_features
exponential kernel	$k(x,y)=exp(- \frac{\|\|x-y\|\|}{2\sigma^2})$
laplacian kernel	$k(x,y)=exp(- \frac{\|\|x-y\|\|}{\sigma})$
ANOVA kernel	$k(x,y)=\sum_{k=1}^nexp(-\sigma(x^k-y^k)^2)^d$	回归
hyberbolic tangent (sigmoid)kernel	$k(x,y)=tanh(\alpha x^Ty+c)$	主要用于神经网络; 正常 alpha=1/N,N是数据维度；alpha>0,c<0; 非正定核
rational quadratic kernel	$k(x,y)=1-\frac{\|\|x-y\|\|^2}{\left \\| x-y \right \\|^2+c}$	有理二次核的计算量比高斯核小，当使用高斯核代价太大时，它可以作为一种选择
Multiquadric Kernel	$k(x,y)=\sqrt{\left \\| x-y \right \\|^2+c^2}$	非正定核
Inverse Multiquadric Kernel	$k(x,y)=\frac{1}{\sqrt{\left \\| x-y \right \\|^2+c^2}}$	与高斯核一样，其结果是一个满秩的核矩阵，从而形成一个无限维的特征空间
Circular Kernel	$k(x,y)=\frac{2}{\pi}arccos(-\frac{\|\|x-y\|\|}{\sigma})-\frac{2}{\pi}\frac{\|\|x-y\|\|}{\sigma}\sqrt{1-(\frac{\|\|x-y\|\|}{\sigma})^2}$ if $\|\|x-y\|\|<\sigma$ , zero otherwise	圆核用于地球静力学应用。它是一个各向同性固定核的例子，在R2中是正定的
Spherical Kernel	$k(x,y)=1-\frac{3}{2}\frac{\|\|x-y\|\|}{\sigma}+\frac{1}{2}(\frac{\|\|x-y\|\|}{\sigma})^3$ if $\|\|x-y\|\|<\sigma$ , zero otherwise	球核与圆核相似，但在R3中是正定的
Wave Kernel		对称正半定
Power Kernel	$k(x,y)=-\|\|x-y\|\|^d$	幂核也称为三角核。它是尺度不变核的一个例子，并且也是条件正定的。
Log Kernel	$k(x,y)=-log(\|\|x-y\|\|^d+1)$	对于图像来说，Log内核似乎特别有趣，但它只是在一定条件下是正的
Spline Kernel	$k(x,y)=1+xy+xy\min(x,y)-\frac{x+y}{2}\min(x,y)^2+\frac{1}{3}\min(x,y)^3$ $k(x,y)=\prod_{i=1}^d 1+x_iy_i+x_iy_i\min(x_i,y_i)-\frac{x_i+y_i}{2}\min(x_i,y_i)^2+\frac{1}{3}\min(x_i,y_i)^3$ $x,y\in\mathbb{R}^d$	以分段三次多项式的形式给出
B-Spline (Radial Basis Function) Kernel	$k(x,y)=B_{2p+1}(x-y),p\in N,B_{i+1}=B_i \otimes B_0$	b样条核是在区间[- 1,1]上定义的
Bessel Kernel
Cauchy Kernel		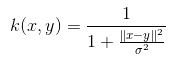一个长尾核，可用于在高维空间上提供远程影响和灵敏度。
Chi-Square Kernel	修订版：
Histogram Intersection Kernel		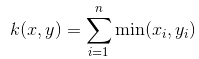直方图相交核也被称为最小核，并已被证明在图像分类中是有用的
Generalized Histogram Intersection		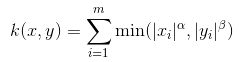广义直方图相交核是在直方图相交核的基础上建立的，用于图像分类，但适用于更广泛的环境
Generalized T-Student Kernel		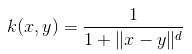是一个Mercel核，因此具有一个正半定核矩阵
Bayesian Kernel
Wavelet Kernel	平移不变版：	a和c分别为小波扩张系数和平移系数