1. 简介
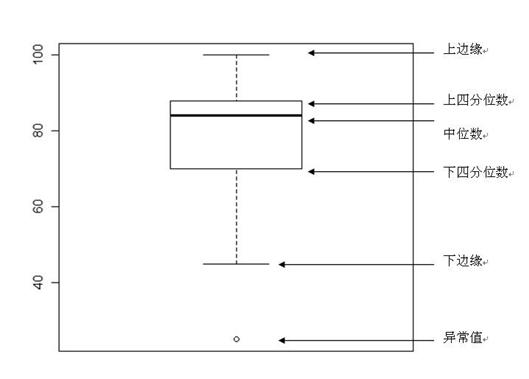
箱形图,又称为盒须图、盒式图、盒状图或箱线图,是一种用作显示一组数据分散情况资料的统计图。箱形图于1977年由美国著名统计学家约翰·图基(John Tukey)发明。它能显示出一组数据的最大值、最小值、中位数、上下四分位数及异常值。

2. Matlab boxplot命令
boxplot(X):产生矩阵X的每一列的盒图和“须”图,“须”是从盒的尾部延伸出来,并表示盒外数据长度的线,如果“须”的外面没有数据,则在“须”的底部有一个点。
boxplot(X,notch):当notch=1时,产生一凹盒图,notch=0时产生一矩箱图。 默认为0.
boxplot(X,notch,‘sym’):sym表示图形符号,默认值为“+”。
boxplot(X,notch,‘sym’,vert) %当vert=0时,生成水平盒图,vert=1时,生成竖直盒图(默认值vert=1)。
boxplot(X,notch,‘sym’,vert,whis) %whis定义“须”图的长度,默认值为1.5,若whis=0则boxplot函数通过绘制sym符号图来显示盒外的所有数据值
2.1 相同大小(行数相同)数据绘图
clc
clear all
close allrng default % For reproducibility
x = randn(100,25);
figuresubplot(2,1,1)
boxplot(x)subplot(2,1,2)
boxplot(x,'PlotStyle','compact')
2.2 不同大小(行数不同)数据绘图
命令:boxplot(x,g)
其中,x为n*1的数据,g为数据的分组(或标签)。
clc
clear all
close allx = rand(50,1);
y = rand(30,1);
z = rand(55,1);
% group = [repmat(1, size(x,1), 1); repmat(2, size(y,1), 1); repmat(3, size(z,1), 1)];
group = [repmat('x', size(x,1), 1); repmat('y', size(y,1), 1); repmat('z', size(z,1), 1)];
boxplot([x;y;z], group);
2.3 提取boxplot绘图中的中值、最大、最小值、异常值等
boxplot返回不同图形对象的句柄数组。
默认参数,输出是7 x M个句柄数组,其中M是boxplot组的数量(即箱型图的数量),每个都有以下7个句柄,分别如下:
1.Upper Whisker
2.lower Whisker
3.Upper Adjacent value
4.Lower Adjacent value
5.Box
6.Median
7.Outliers
在不同的参数下,boxplot可能会返回不同数量的句柄,因此最好通过标记找到所需的内容。
要提取数据,您必须访问特定对象的Data属性(如果此属性存在)。
例子:
clc
clear all
close allx1 = [10 12 9 8 12 11 15 12 34 12 9];
x2 = [13 14 6 9 18 16 47 18 54 13 6];figure
boxplot([x1' x2'])
第一组数据中异常值 34,第二组数据异常值为47 和 54。现在我们提取这几个异常数据。
h = findobj(gcf,'tag','Outliers');
xdata = get(h,'XData')
ydata = get(h,'YData')即可得到异常值在窗口中的x轴值和y轴值。
也可以使用下面的代码获得这些数据,推荐使用这种方法获得!
outlier = get(h(7),'YData');
media = get(h(6),'YData');
minv = get(h(4),'YData');
maxv = get(h(3),'YData');2.4 指定x轴位置绘制box
X = [1.2 1.8 3.2 3.8 5.2 5.8];
Y = rand(100, 6);
boxplot(Y, 'positions', X, 'labels', X)
2.5 不同数据大小指定x轴位置绘图
clc
clear all
close allx0 = [9 10 12 9 8 12 11 16 12 10];
x1 = [1 10 12 9 8 12 11 15 12 34 12 7];
x2 = [8 13 14 6 9 18 16 47 18 54 13 6 8];
x = [x0';x1';x2'];
g = [repmat(1,length(x0),1);repmat(2,length(x1),1);repmat(3,length(x2),1)];
pos = [1.5 2 5];
boxplot(x,g,'positions', pos, 'labels', pos)
3. 异常值判别方法
判断异常值,需要明白几个概念,什么是异常值?什么是分位数?
3.1 异常值
是位于数据系列中的极端值,该异常值非常小或非常大,因此可能影响数据系列的整体。异常值通常被视为极值,由于其极高或极低的值而可能影响整体,因此应从数据中丢弃。
异常值也可以表示为位于分布的整体之外的值,因此可以影响整个数据系列。异常值通常被认为是由于存在可能低估或高估研究的极值而导致测量误差的原因,因为它与来自群体的随机样本中的其他值具有异常距离。
根据所有统计学家遵循的基本标准,对异常值的通用定义是落在第三个四分位数之上或低于第一个四分位数的四分位数距的1.5倍以上。
3.2 四分位数
分位数是将总体的全部数据按大小顺序排列后,处于各等分位置的变量值。如果将全部数据分成相等的两部分,它就是中位数;如果分成四等分,就是四分位数。四分位数有三个,第一个四分位数就是通常所说的四分位数,称为下四分位数,第二个四分位数就是中位数,第三个四分位数称为上四分位数,分别用Q1、Q2、Q3表示。
第一四分位数 (Q1),又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
第二四分位数 (Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
第三四分位数 (Q3),又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。
第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range,IQR)。
3.3 确定异常值

因此,任何超过上限或小于下限的值都将是异常值。 只有位于下限和上限内的数据在统计上被认为是正常的,因此可用于进一步观察或研究。
3.4 例子
设数据范围为199,201,236,269,271,278,283,291,301,303和341
因此n = 11


因此很明显,任何高于333.5或低于201.5的范围都是异常值。 因此,在数据系列199,201,236,269,271,278,283,291,301,303,341中,异常值分别为199,201和341.这三个值位于任何一个极值上都可以认为是异常的,应该从整个系列中丢弃。 任何对这个系列的分析都不受这些极端值的影响。 因此,丢弃异常值后应考虑进一步观察或研究的数据系列如下。
236,269,271,278,283,291,301,303
4. 获取统计信息的两种方法
下面两个函数实现的功能一样,都是从一组数据中获取最小最大中值均值标准差和异常值。函数1从boxplot出发,获取图形中这些统计数据,函数2直接进行计算根据定义判断异常值,求剩余数据的统计信息。函数1和函数2功能一样,效率不同,函数1效率极低。
4.1 函数1
% 1.Upper Whisker
% 2.lower Whisker
% 3.Upper Adjacent value
% 4.Lower Adjacent value
% 5.Box
% 6.Median
% 7.Outliers% X_n*1
% x0 = [9 10 12 9 8 12 11 16 12 10 12 9 7];
% x1 = [1 10 12 9 8 12 11 15 12 34 12 9 7];
% x2 = [8 13 14 6 9 18 16 47 18 54 13 6 8];
% [minv,maxv,media, meanv, outlier] = boxvalue(x0')function [minv, maxv, medi, meanv, stdv, outlier] = boxvalue(x)
meanv = [];
stdv = [];
if isempty(x)minv = nan;maxv = nan;medi = nan;meanv = nan;stdv = nan;outlier = nan;
return;
endfigure(11)h = boxplot(x);
medi = get(h(6),'YData'); medi = medi(1);
minv = get(h(4),'YData'); minv = minv(1);
maxv = get(h(3),'YData'); maxv = maxv(1);
outlier = get(h(7),'YData');%无异常值情况
if length(outlier)==1 & isnan(outlier)meanv = mean(x);stdv = std(x);close 11return;
end%有异常值情况
ids = [];
outlier = unique(outlier);
for i=1:length(outlier)ids = [ids find(x==outlier(i))'];
end
ids = sort(ids,'descend');
for i=1:length(ids)x(ids(i)) = [];
end
stdv = std(x);
meanv = mean(x);
close 11
end4.2 函数2
function [minv, maxv, medi, meanv, stdv, outlier] = statistic(x)
minv = nan;
maxv = nan;
medi = nan;
meanv = nan;
stdv = nan;
outlier = nan;
if isempty(x)return;
endQ = quantile(x,[0.25 0.75]);
Q1 = Q(1);
Q3 = Q(2);
IQR = Q3-Q1;low_limit = Q1-1.5*IQR;
upp_limit = Q3+1.5*IQR;
low_ids = x<=low_limit;
upp_ids = x>=upp_limit;ids = ~low_ids & ~upp_ids;
if sum(ids)==0return;
end
val = x(ids);minv = min(val);
maxv = max(val);
medi = median(val);
stdv = std(val);
meanv = mean(val);
outlier = x(low_ids | upp_ids);
end
https://www.whatissixsigma.net/box-plot-diagram-to-identify-outliers/
https://socratic.org/questions/how-do-you-calculate-outliers-when-drawing-box-plots
参考
https://ww2.mathworks.cn/help/stats/boxplot.html
https://www.jianshu.com/p/bf3d1a74b45d
https://stackoverflow.com/questions/9728970/matlab-extract-values-from-boxplot
https://blog.csdn.net/wokaowokaowokao12345/article/details/92718896