引言

关于B树的性质

一、B树的结构

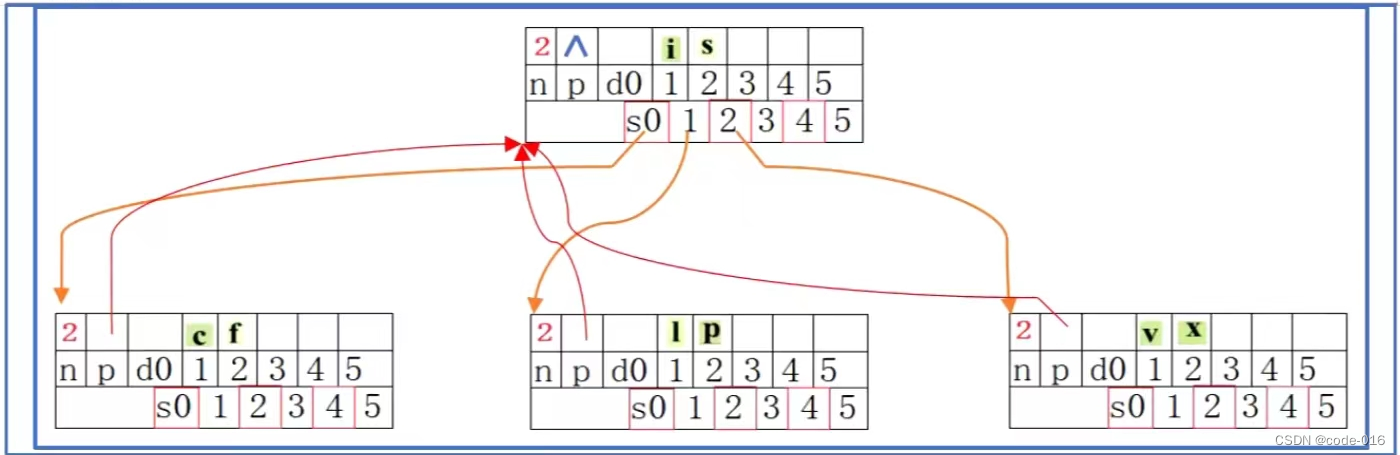
二、B树的实现

#include<iostream>
using namespace std;
#if 1
//5分支Btree
#define M 5	//奇数
#define MAXSIZE (M-1)	//最多元素个数
#define MINSIZE (M/2)	//最少元素个数	//B树
class Btree
{
public://关键码类型using KeyType = char;//元素类型typedef struct {KeyType key;	//关键码void* infoptr;	//记录集}ElemType;//树结点类型typedef struct BNode{int keysize;				//当前结点中data中挂接关键码的个数struct BNode* parent;		//指向双亲结点ElemType data[M + 1];		//结点下的元素{关键码，记录集}struct BNode* sub[M + 1];	//分支链}BNode;//查询的结果类型class ResultNode {public:BNode* pnode;	//关键码所在的树结点地址int index;		//关键码所在pnode->data的前一个下标bool tag;		//是否存在的标志位 存在true,不存在false;public:ResultNode() :pnode(nullptr), index(-1), tag(false) {}~ResultNode() {}};//申请BNode结点BNode* BuyBNode(){BNode* s = (BNode*)malloc(sizeof(BNode));if (nullptr == s) exit(-1);memset(s, 0, sizeof(BNode));return s;}//申请并初始化根节点BNode* MakeRoot(const ElemType& item, BNode* left, BNode* right){BNode* root = BuyBNode();root->keysize = 1;root->parent = nullptr;root->data[1] = item;if (nullptr != left) {left->parent = root;}if (nullptr != right){right->parent = root;}root->sub[0] = left;root->sub[1] = right;return root;}//pos位置插入item操作void Insert_Item(BNode* ptr, int pos, const ElemType& item, BNode* right){for (int i = ptr->keysize; i > pos; --i){ptr->data[i + 1] = ptr->data[i];ptr->sub[i + 1] = ptr->sub[i];}ptr->data[pos + 1] = item;ptr->sub[pos + 1] = right;++ptr->keysize;}//将ptr中后半截的元素移动到新开辟的s分支中ElemType MoveElem(BNode* s, BNode* ptr, int pos){for (int i = 0, j = pos + 1; j <= ptr->keysize; ++i, ++j){s->data[i] = ptr->data[j];s->sub[i] = ptr->sub[j];if (s->sub[i] != nullptr){s->sub[i]->parent = s;}}ptr->keysize = MINSIZE;s->keysize = MINSIZE;s->parent = ptr->parent;return s->data[0];	//返回哨兵结点的elem}//分裂产生返回新根节点BNode* SplitNewRoot(BNode* ptr){BNode* s = BuyBNode();//将ptr中后半截的元素移动到新开辟的s分支中ElemType item = MoveElem(s, ptr, MINSIZE);if (nullptr == ptr->parent){return MakeRoot(item, ptr, s);}//将item在ptr->parent结点中再进行找位置，插入，再分裂BNode* pa = ptr->parent;int pos = pa->keysize;pa->data[0] = item;	//哨兵位填充while (pos > 0 && item.key < pa->data[pos].key){--pos;}//s是pa的右孩子Insert_Item(pa, pos, item, s);//pa分支满了，对pa进行递归分裂if (pa->keysize > MAXSIZE){return SplitNewRoot(pa);}else{return nullptr;}}
private:BNode* root;	//根节点int size;		//当前树的关键码的个数
public:Btree() :root(nullptr), size(0) {}~Btree() {}//得到root结点地址BNode* GetRoot()const{return root;}//查找关键码ResultNode FindKey(KeyType ch){ResultNode res;	//默认构造nullptr, -1, false;BNode* p = root;while (p != nullptr){p->data[0].key = ch;int index = p->keysize;		//逆序查询while (index > 0 && ch < p->data[index].key){--index;}res.pnode = p;			//结果指向当前的树结点res.index = index;//找到了if (index > 0 && ch == p->data[index].key){res.tag = true;break;}p = p->sub[index];}return res;}//插入ElemTypebool Insert(const ElemType& item){if (nullptr == root){root = MakeRoot(item, nullptr, nullptr);size = 1;return true;}//查找item.key是否存在ResultNode res = FindKey(item.key);//说明已经存在if (res.pnode != nullptr && res.tag) return false;//不存在，从find的res.pnode开始进行插入BNode* ptr = res.pnode;//插入位置int pos = res.index;//插入并后移元素Insert_Item(ptr, pos, item, nullptr);//插入元素后个数 > MAXSIZE，需要分裂重生出新根节点if (nullptr != ptr && ptr->keysize > MAXSIZE){BNode* newroot = SplitNewRoot(ptr);//根节点改变if (newroot != nullptr){root = newroot;}}++size;return true;}//有序输出B树中的所有元素void BTreeShow(BNode* ptr){if (nullptr == ptr) return;BTreeShow(ptr->sub[0]);for (int i = 1; i <= ptr->keysize; ++i){cout << ptr->data[i].key;BTreeShow(ptr->sub[i]);}}
};

三、插入、查询、输出测试

//测试
int main()
{Btree::KeyType ch[] = {"heqwertsycjgkzlxlowrd"};Btree bt;int i = 0;while(ch[i] != '\0'){Btree::ElemType tmp = { ch[i], nullptr };cout << bt.Insert(tmp);++i;}cout << endl;bt.BTreeShow(bt.GetRoot());return 0;
}