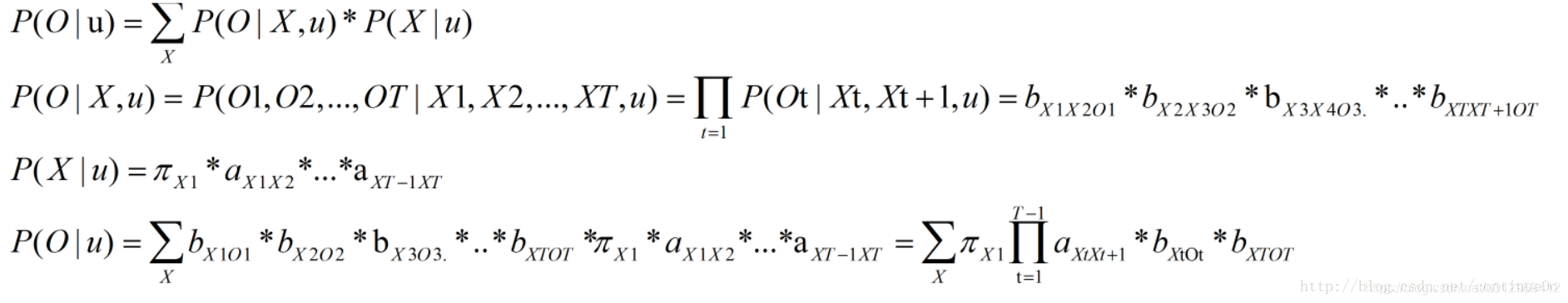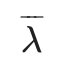1. 马尔科夫链

在机器学习算法中，马尔可夫链(Markov chain)是个很重要的概念。马尔可夫链（Markov chain），⼜称离散时间马尔可夫链（discrete-time Markov chain），因俄国数学家安德烈·⻢尔可夫（俄语：Андрей Андреевич Марков）得名。

1.1 简介

马尔科夫链即为状态空间中从⼀个状态到另⼀个状态转换的随机过程。

1.2 经典举例

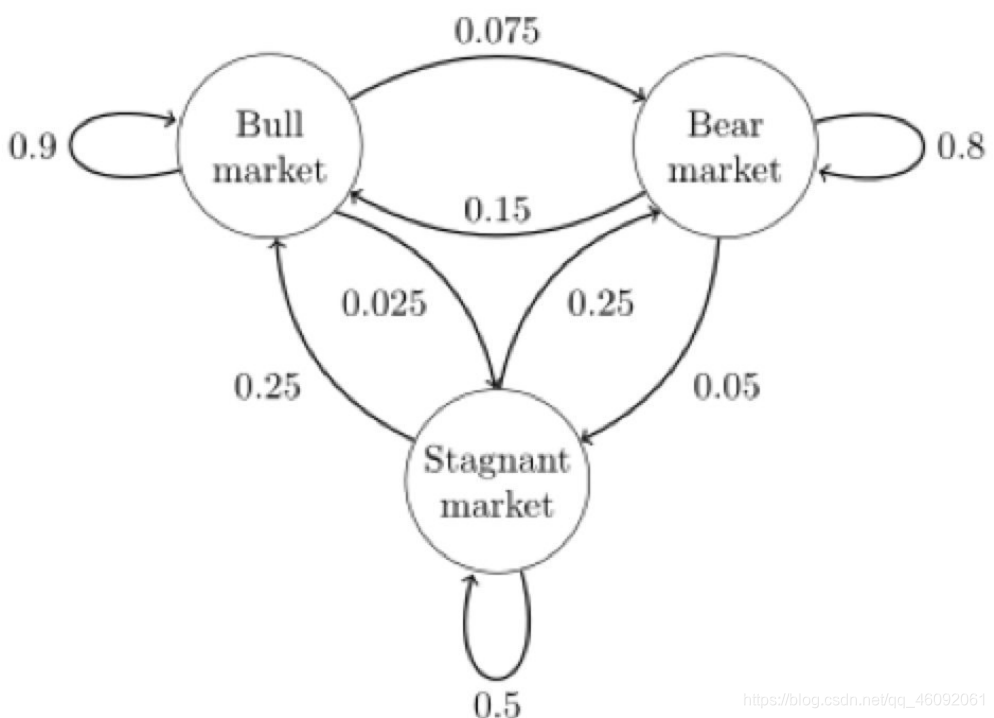
下图中的马尔科夫链是⽤来表示股市模型，共有三种状态：⽜市（Bull market）, 熊市（Bear market）和横盘 （Stagnant market）。

每⼀个状态都以⼀定的概率转化到下⼀个状态。比如，牛市以0.025的概率转化到横盘的状态。

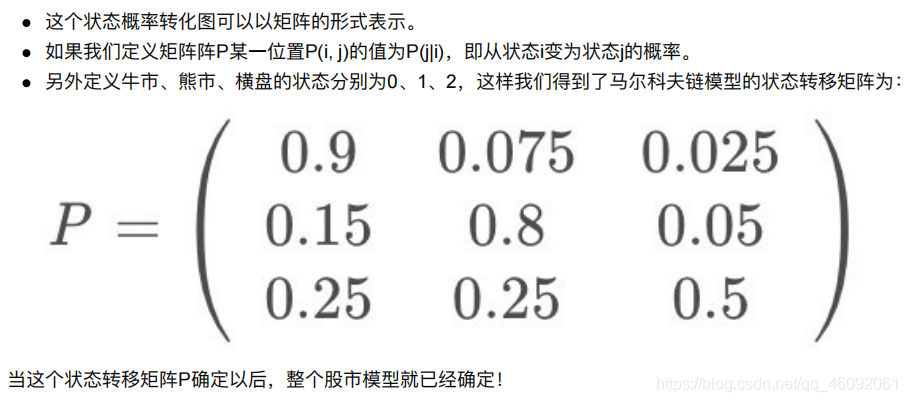
1.3 小结

• 马尔科夫链即为
  • 状态空间中从⼀个状态到另⼀个状态转换的随机过程。
  • 该过程要求具备“⽆记忆”的性质：
    • 下⼀状态的概率分布只能由当前状态决定，在时间序列中它前⾯的事件均与之⽆关。

2. HMM简介

隐⻢尔可夫模型（Hidden Markov Model，HMM）是统计模型，它⽤来描述⼀个含有隐含未知参数的⻢尔可夫过程。 其难点是从可观察的参数中确定该过程的隐含参数。然后利⽤这些参数来作进⼀步的分析，例如模式识别。

2.1 简单案例

下⾯我们⼀起⽤⼀个简单的例⼦来阐述：

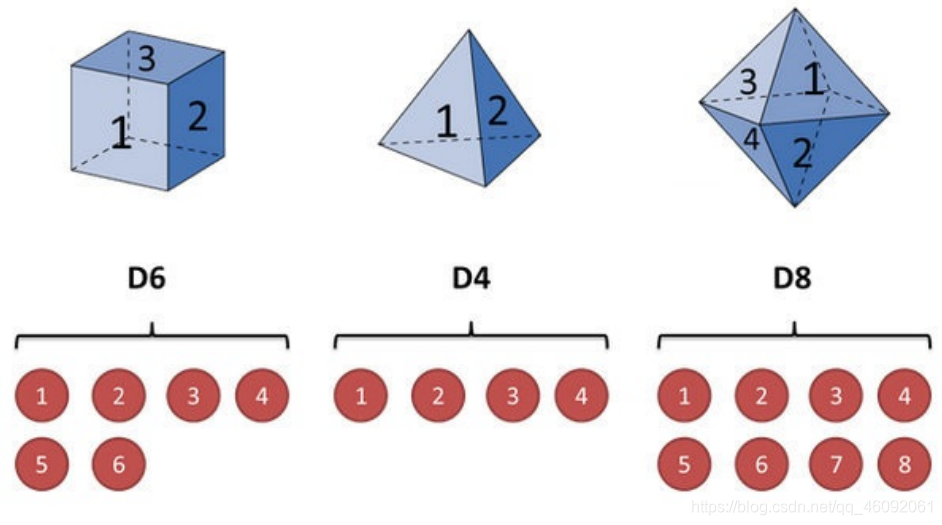
• 假设我⼿⾥有三个不同的骰⼦。
  • 第⼀个骰⼦是我们平常⻅的骰⼦（称这个骰⼦为D6），6个⾯，每个⾯（1，2，3，4，5，6）出现的概率是 1/6。
  • 第⼆个骰⼦是个四⾯体（称这个骰⼦为D4），每个⾯（1，2，3，4）出现的概率是1/4。
  • 第三个骰⼦有⼋个⾯（称这个骰⼦为D8），每个⾯（1，2，3，4，5，6，7，8）出现的概率是1/8。

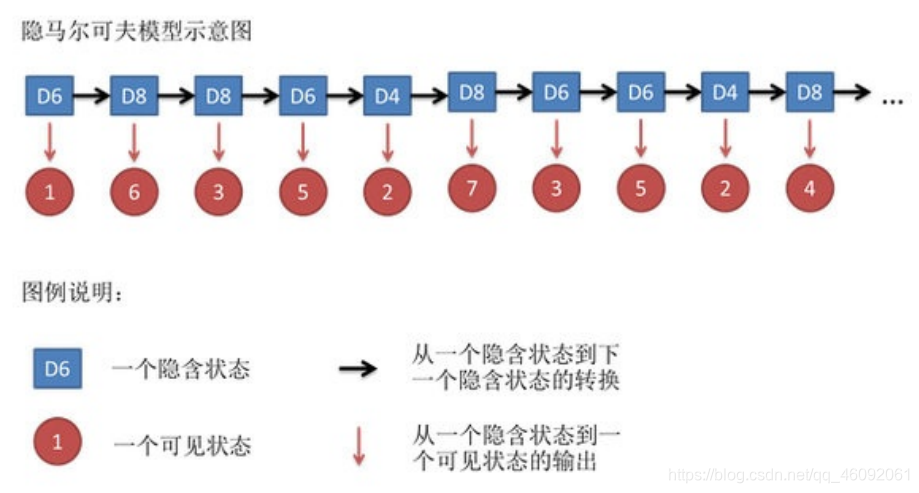
其实对于HMM来说，如果提前知道所有隐含状态之间的转换概率和所有隐含状态到所有可见状态之间的输出概率，做 模拟是相当容易的。但是应⽤HMM模型时候呢，往往是缺失了⼀部分信息的。

• 有时候你知道骰⼦有⼏种，每种骰⼦是什么，但是不知道掷出来的骰⼦序列；
• 有时候你只是看到了很多次掷骰⼦的结果，剩下的什么都不知道。

如果应⽤算法去估计这些缺失的信息，就成了⼀个很重要的问题。

2.2 案例进阶

2.2.1 问题阐述

2.2.2 问题解决

2.2.2.1 一个简单问题【对应问题2】

其实这个问题实⽤价值不⾼。由于对下⾯较难的问题有帮助，所以先在这⾥提⼀下。

• 知道骰⼦有⼏种，每种骰⼦是什么，每次掷的都是什么骰⼦，根据掷骰⼦掷出的结果，求产⽣这个结果的概率。
  

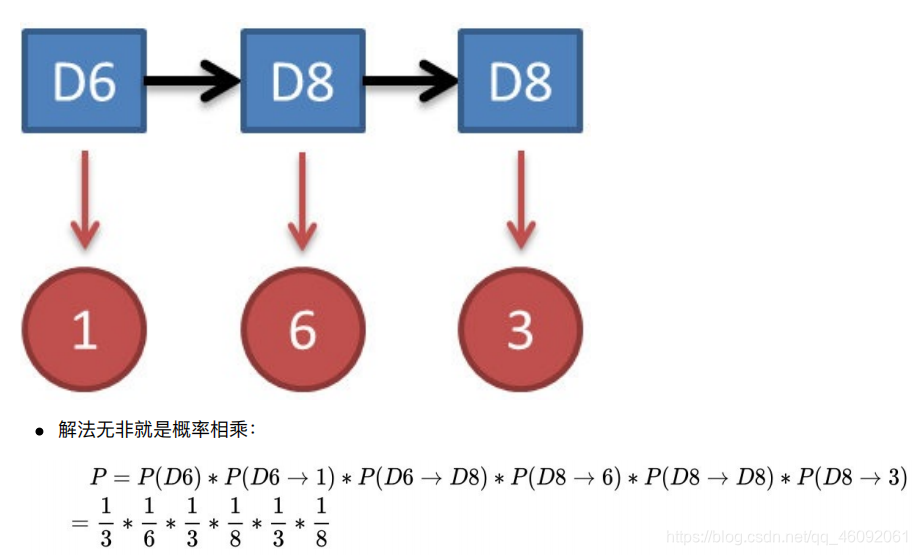
2.2.2.2 看见不可见的，破解骰子序列【对应问题1】

写到这⾥，⼤家应该看出点规律了。既然掷骰⼦⼀、⼆、三次可以算，掷多少次都可以以此类推。 我们发现，我们要求最⼤概率骰⼦序列时要做这么⼏件事情。

• ⾸先，不管序列多⻓，要从序列⻓度为1算起，算序列⻓度为1时取到每个骰⼦的最⼤概率。
• 然后，逐渐增加⻓度，每增加⼀次⻓度，重新算⼀遍在这个⻓度下最后⼀个位置取到每个骰⼦的最⼤概率。因为上 ⼀个⻓度下的取到每个骰⼦的最⼤概率都算过了，重新计算的话其实不难。
• 当我们算到最后⼀位时，就知道最后⼀位是哪个骰⼦的概率最⼤了。然后，我们要把对应这个最⼤概率的序列从后往前推出来。

2.2.2.3 谁动了我的骰子？【对应问题3】

⽐如说你怀疑⾃⼰的六⾯骰被赌场动过⼿脚了，有可能被换成另⼀种六⾯骰，这种六⾯骰掷出来是1的概率更⼤，是 1/2，掷出来是2，3，4，5，6的概率是1/10。你怎么办么？

• 答案很简单，算⼀算正常的三个骰⼦掷出⼀段序列的概率，再算⼀算不正常的六⾯骰和另外两个正常骰⼦掷出这段序列的概率。如果前者⽐后者⼩，你就要⼩⼼了。

⽐如说掷骰⼦的结果是：

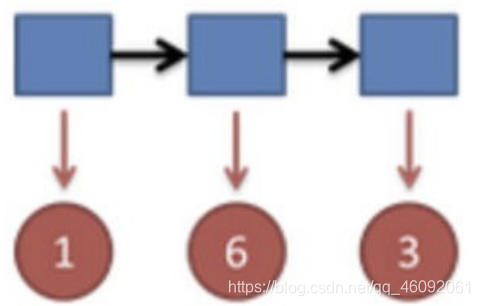
要算⽤正常的三个骰⼦掷出这个结果的概率，其实就是将所有可能情况的概率进⾏加和计算。

同样，简单⽽暴⼒的⽅法就是把穷举所有的骰⼦序列，还是计算每个骰⼦序列对应的概率，但是这回，我们不挑最⼤值 了，⽽是把所有算出来的概率相加，得到的总概率就是我们要求的结果。这个⽅法依然不能应⽤于太⻓的骰⼦序列（⻢ 尔可夫链）。 我们会应⽤⼀个和前⼀个问题类似的解法，只不过前⼀个问题关⼼的是概率最⼤值，这个问题关⼼的是概率之和。解决这个问题的算法叫做前向算法（forward algorithm）。

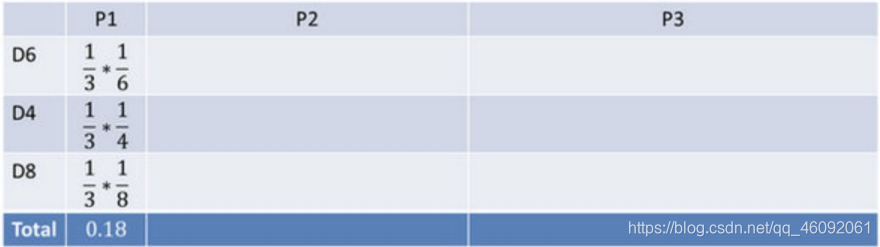
⾸先，如果我们只掷⼀次骰⼦：

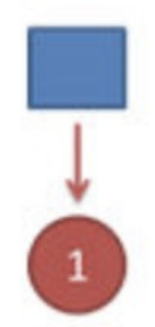
看到结果为1.产⽣这个结果的总概率可以按照如下计算，总概率为0.18：

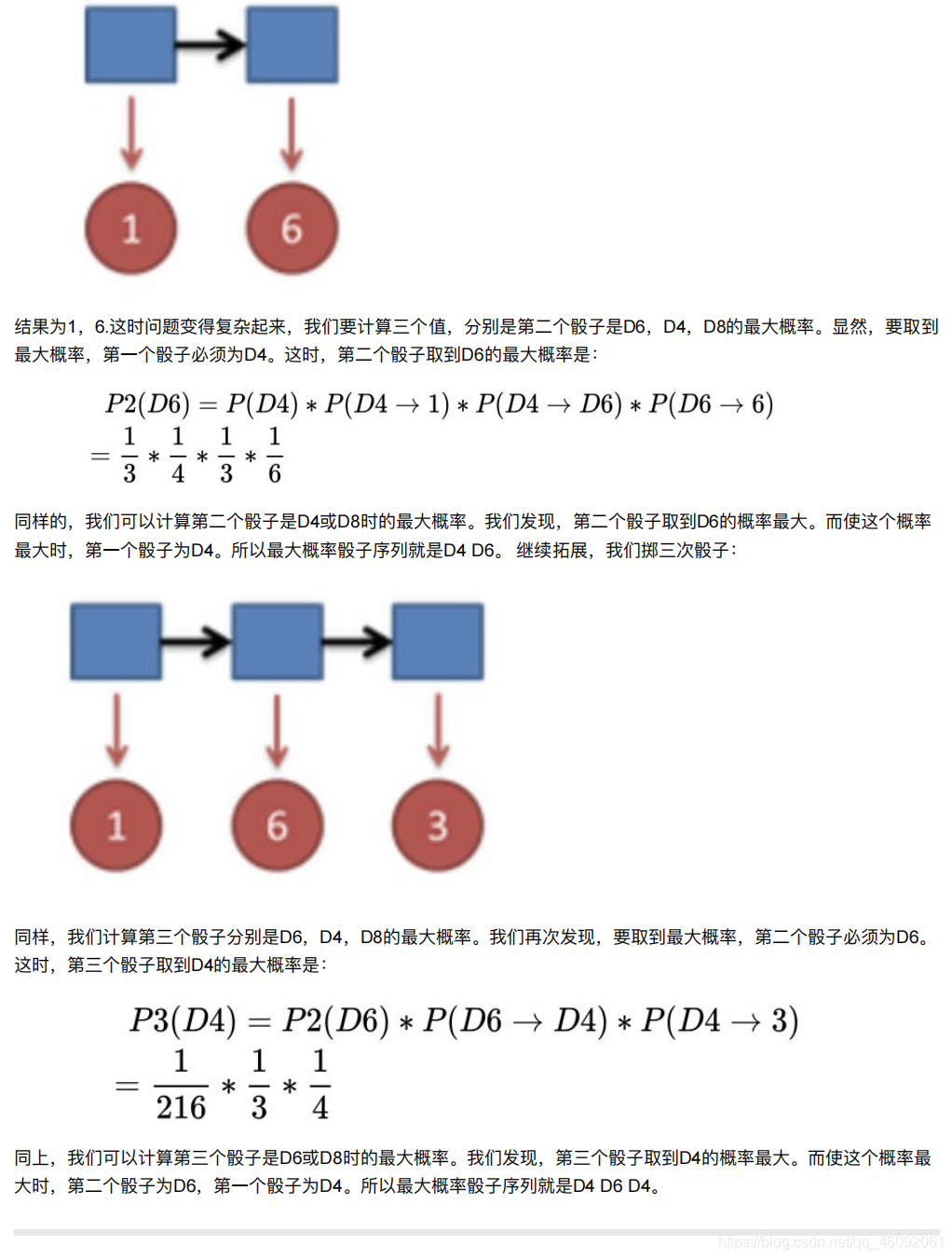
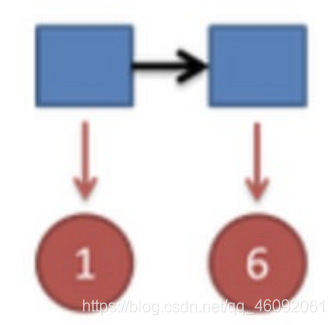
把这个情况拓展，我们掷两次骰子：

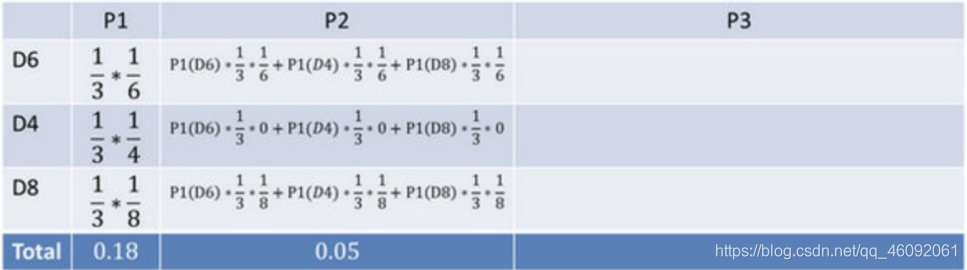
看到结果为1，6.产⽣这个结果的总概率可以按照如下计算，总概率为0.05：

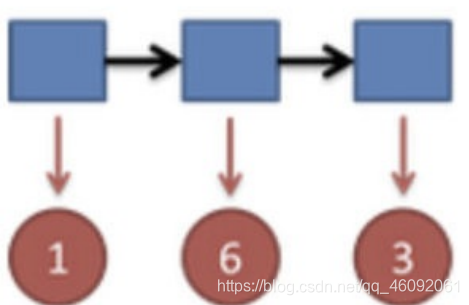
继续拓展，我们掷三次骰⼦：

看到结果为1，6，3.产⽣这个结果的总概率可以按照如下计算，总概率为0.03：

同样的，我们⼀步⼀步的算，有多长算多长，再⻓的⻢尔可夫链总能算出来的。

⽤同样的⽅法，也可以算出不正常的六⾯骰和另外两个正常骰⼦掷出这段序列的概率，然后我们⽐较⼀下这两个概率⼤ ⼩，就能知道你的骰⼦是不是被⼈换了。

2.3 小结

• 隐马尔可夫模型（Hidden Markov Model，HMM）是统计模型，它⽤来描述⼀个含有隐含未知参数的⻢尔可夫过程。
• 常见术语
  • 可见状态链
  • 隐含状态链
  • 转换概率
  • 输出概率

3. HMM模型基础

3.1 什么样的问题需要HMM模型

3.2 HMM模型的定义

HMM模型做了两个很重要的假设如下：

1） 齐次马尔科夫链假设。

2） 观测独立性假设。

3.3 一个HMM模型实例

下⾯我们⽤⼀个简单的实例来描述上⾯抽象出的HMM模型。这是⼀个盒⼦与球的模型。

例⼦来源于李航的《统计学习方法》。

假设我们有3个盒⼦，每个盒⼦⾥都有红⾊和⽩⾊两种球，这三个盒⼦里球的数量分别是：

按照下⾯的⽅法从盒⼦⾥抽球，开始的时候，

• 从第⼀个盒⼦抽球的概率是0.2，
• 从第⼆个盒⼦抽球的概率是0.4，
• 从第三个盒⼦抽球的概率是0.4。

3.4 HMM观测序列的生成

3.5 HMM模型的三个基本问题

3.4 小结

• 什么样的问题可以⽤HMM模型解决
  • 基于序列的，⽐如时间序列；
  • 问题中包含两类数据，⼀类是可以观测到的观测序列；另⼀类是不能观察到的隐藏状态序列。
• HMM模型的两个重要假设
  • 其次⻢尔科夫链假设
  • 观测独⽴性假设
• HMM模型的三个基本问题
  • 评估观察序列概率—— 前向后向的概率计算
  • 预测问题，也称为解码问题 ——维特⽐（Viterbi）算法
  • 模型参数学习问题 —— 鲍姆-⻙尔奇（Baum-Welch）算法

4. 前向后向算法评估观察序列概率

4.1 回顾HMM问题⼀：求观测序列的概率

4.2 用前向算法求HMM观测序列的概率

前向后向算法是前向算法和后向算法的统称，这两个算法都可以⽤来求HMM观测序列的概率。我们先来看看前向算法 是如何求解这个问题的。

4.2.1 流程梳理

4.2.2 算法总结

从递推公式可以看出，我们的算法时间复杂度是O(TN2)，比暴⼒解法的时间复杂度O(T NT )少了⼏个数量级。

4.3 HMM前向算法求解实例

4.4 用后向算法求HMM观测序列的概率

4.4.1 流程梳理

熟悉了⽤前向算法求HMM观测序列的概率，现在我们再来看看怎么⽤后向算法求HMM观测序列的概率。

后向算法和前向算法⾮常类似，都是⽤的动态规划，唯⼀的区别是选择的局部状态不同，后向算法⽤的是“后向概率”。

4.4.2 后向算法流程

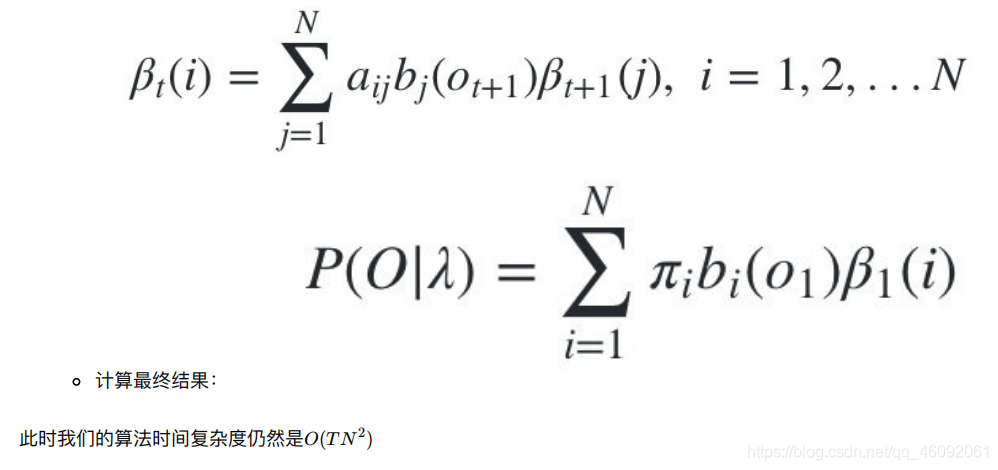
4.5 小结

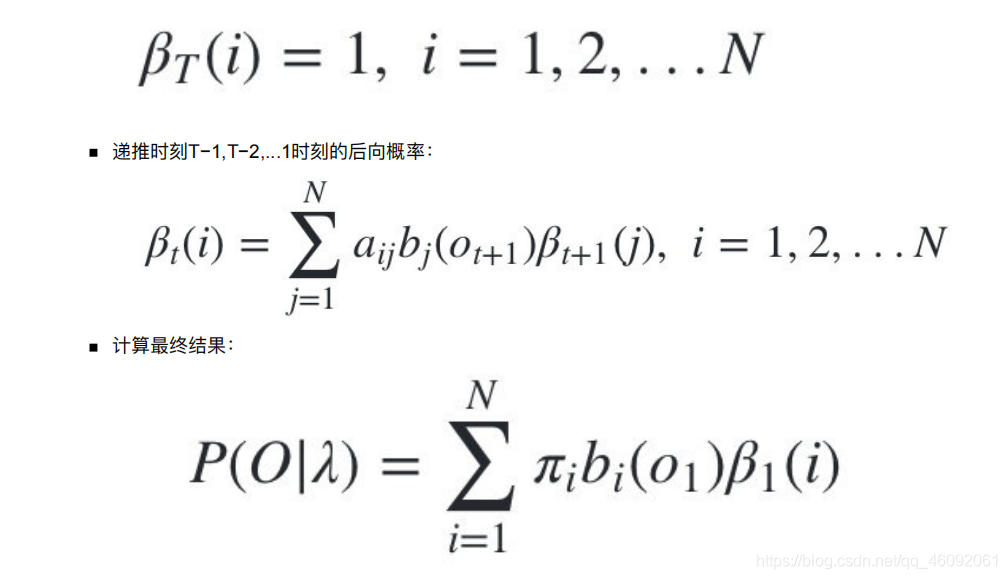
5. 维特比算法解码隐藏状态序列

学习⽬标

• 知道维特⽐算法解码隐藏状态序列

在本篇我们会讨论维特⽐算法解码隐藏状态序列，即给定模型和观测序列，求给定观测序列条件下，最可能出现的对应 的隐藏状态序列。

HMM模型的解码问题最常⽤的算法是维特⽐算法，当然也有其他的算法可以求解这个问题。

同时维特⽐算法是⼀个通⽤的求序列最短路径的动态规划算法，也可以⽤于很多其他问题。

5.1 HMM最可能隐藏状态序列求解概述

5.2 维特⽐算法概述

维特⽐算法是⼀个通⽤的解码算法，是基于动态规划的求序列最短路径的⽅法。

既然是动态规划算法，那么就需要找到合适的局部状态，以及局部状态的递推公式。在HMM中，维特⽐算法定义了两 个局部状态⽤于递推。

1. 第⼀个局部状态是在时刻t隐藏状态为i所有可能的状态转移路径i ,i , …i 中的概率最⼤值。

5.3 维特⽐算法流程总结

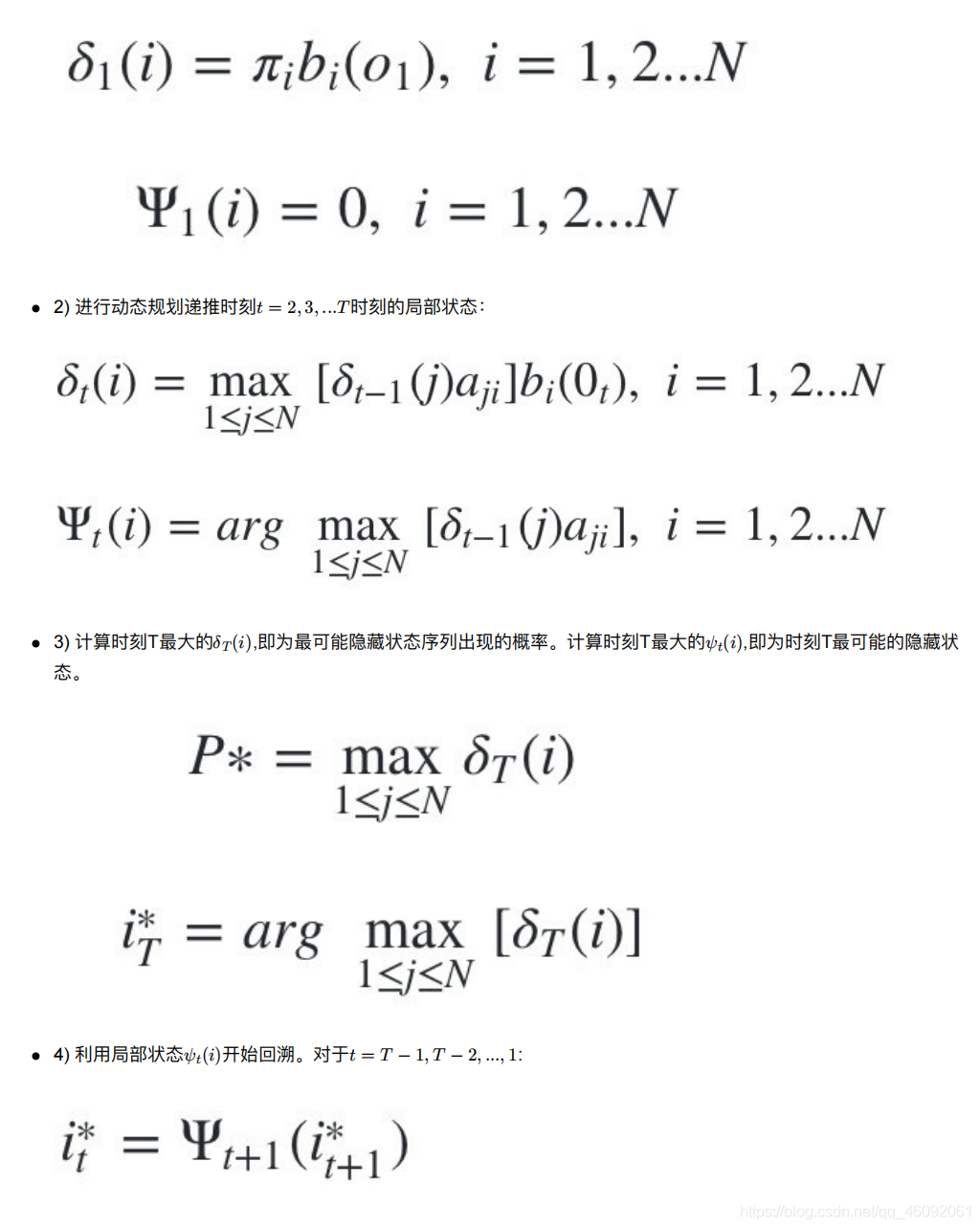
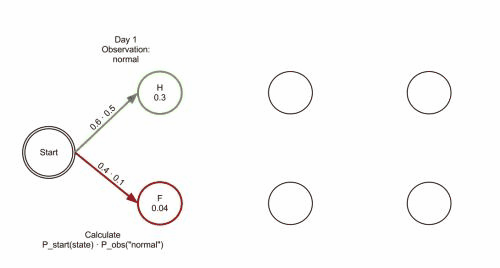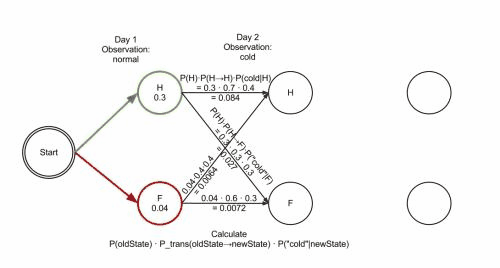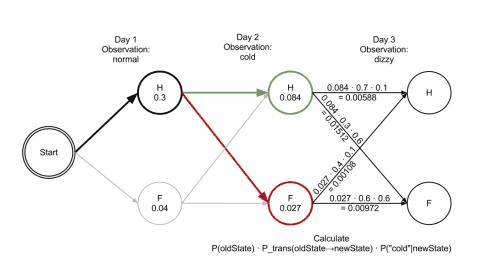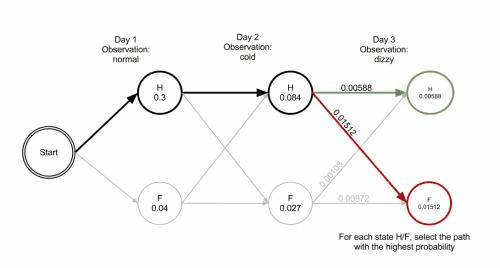
5.4 HMM维特⽐算法求解实例

下⾯我们仍然⽤盒⼦与球的例⼦来看看HMM维特⽐算法求解。 我们的观察集合是:

6. 鲍姆-韦尔奇算法简介

学习⽬标

• 了解鲍姆-⻙尔奇算法

模型参数学习问题 —— 鲍姆-⻙尔奇（Baum-Welch）算法(状态未知) ，

6.2 鲍姆-⻙尔奇算法原理

7. HMM模型API介绍

7.1 API的安装

官⽹链接：https://hmmlearn.readthedocs.io/en/latest/

pip3 install hmmlearn

7.2 hmmlearn介绍

7.3 MultinomialHMM实例

下⾯我们⽤我们在前⾯讲的关于球的那个例⼦使⽤MultinomialHMM跑⼀遍。

import numpy as np 
from hmmlearn import hmm

# 设定隐藏状态的集合 
states = ["box 1", "box 2", "box3"] 
n_states = len(states) # 设定观察状态的集合 
observations = ["red", "white"] 
n_observations = len(observations) # 设定初始状态分布 
start_probability = np.array([0.2, 0.4, 0.4]) # 设定状态转移概率分布矩阵 
transition_probability = np.array([ [0.5, 0.2, 0.3], [0.3, 0.5, 0.2], [0.2, 0.3, 0.5]
])# 设定观测状态概率矩阵 
emission_probability = np.array([ [0.5, 0.5], [0.4, 0.6], [0.7, 0.3] 
])

# 设定模型参数 
model = hmm.MultinomialHMM(n_components=n_states) 
model.startprob_=start_probability # 初始状态分布 
model.transmat_=transition_probability # 状态转移概率分布矩阵 
model.emissionprob_=emission_probability # 观测状态概率矩阵

现在我们来跑⼀跑HMM问题三维特⽐算法的解码过程，使⽤和之前⼀样的观测序列来解码，代码如下：

seen = np.array([[0,1,0]]).T # 设定观测序列 
box = model.predict(seen) print("球的观测顺序为：\n", ", ".join(map(lambda x: observations[x], seen.flatten()))) 
# 注意：需要使⽤flatten⽅法，把seen从⼆维变成⼀维 
print("最可能的隐藏状态序列为:\n"， ", ".join(map(lambda x: states[x], box)))

我们再来看看求HMM问题⼀的观测序列的概率的问题，代码如下：

print(model.score(seen)) # 输出结果是：-2.03854530992

要注意的是score函数返回的是以⾃然对数为底的对数概率值，我们在HMM问题⼀中⼿动计算的结果是未取对数的原始 概率是0.13022。对⽐⼀下：

import math 
math.exp(-2.038545309915233) 
# ln0.13022≈−2.0385 
# 输出结果是：0.13021800000000003

加油!

感谢!

努力!