抽样技术--简单随机抽样

article/2025/9/16 15:42:01

文章目录

  • 简单随机抽样
  • 简单估计量及其性质
    • 对总体均值的估计
      • 简单随机抽样
      • 简单例子
    • 对总体总量的估计
      • 例子
    • 对总体比例的估计
      • 例子
  • 比率估计量及其性质
    • 辅助变量
    • 比率估计量
      • 总体均值的期望咋算
      • 总体均值的方差咋算
      • 总体总值的期望咋算
      • 总体总值的方差咋算
      • 比率估计量的方差咋算
      • Y与X的总体协方差
      • X的总体方差
      • Y与X的总体相关系数
      • Y的相对方差（变异系数）
      • Y与X的相对协方差
      • X的相对方差（变异系数）
  • 回归估计量及其性质
  • 各种估计量的精度的比较
  • 简单随机抽样的实施
    • 总体方差的估计
    • 其他影响因素
    • 设计效果

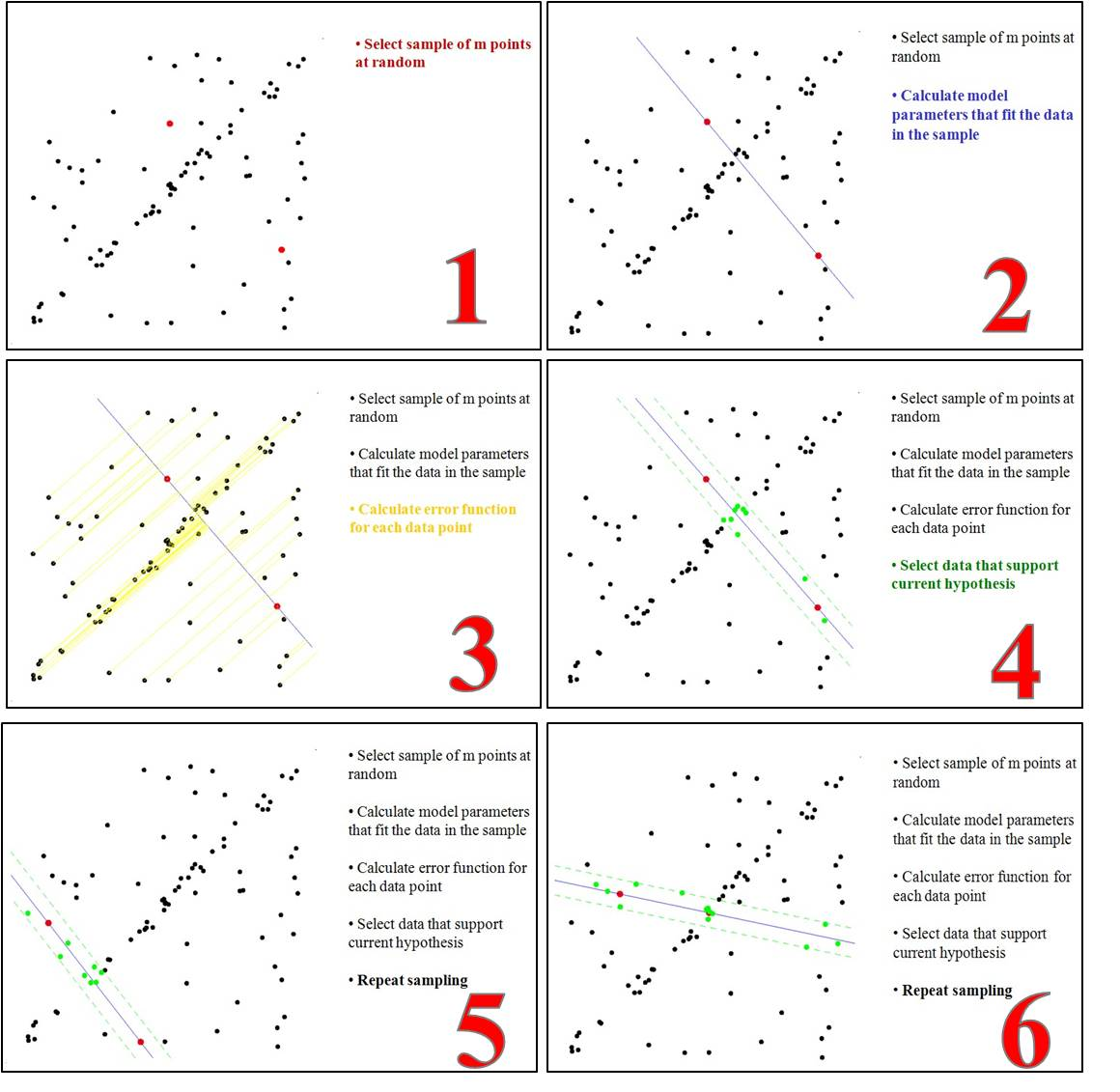
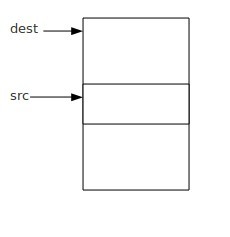
简单随机抽样

一次抽n个、逐次不放回抽n个、从所有的排列组合里抽一个

简单估计量及其性质

对总体均值的估计

简单随机抽样

在简单随机抽样里，咱用样本均值来估计总体均值（这个估计无偏）
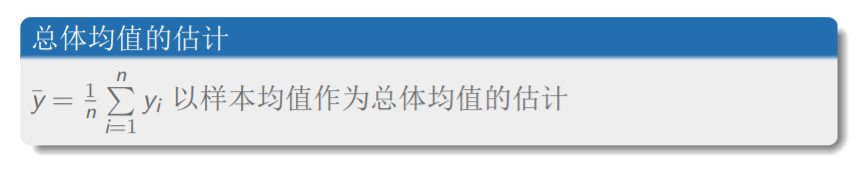
在这里插入图片描述

在简单随机抽样里，样本的方差这样算
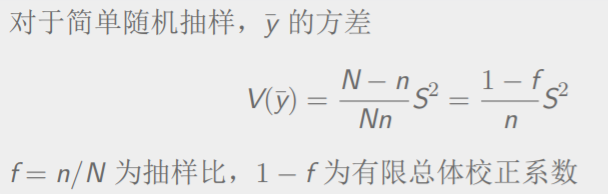
在这里插入图片描述
这样算出来的还是总体方差的无偏估计
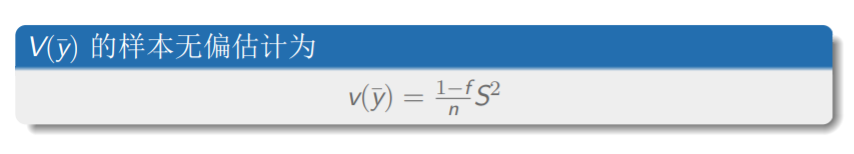
在这里插入图片描述

简单例子

在这里插入图片描述
咱先嗯算一波样本的均值和方差
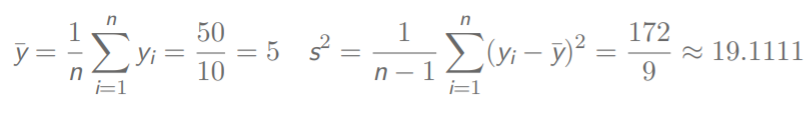
在这里插入图片描述
然后直接用样本的均值和方差来构造总体的均值和方差
在这里插入图片描述
这就算出来了

对总体总量的估计

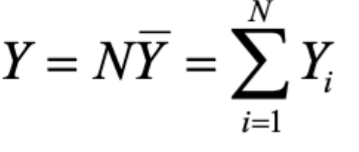
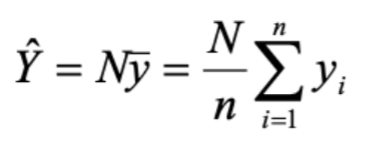
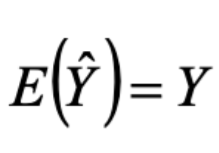
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
上面的一堆公式就是说咱可以用样本的均值算出总体的估计，然后这个估计还是无偏的
在这里插入图片描述
上面这两个公式不知道在讲什么鬼
（其实就是算的如何用样本方差来估计总量估计值的方差）

例子

在这里插入图片描述
首先我们要估计总量，总量就是总体个数*样本均值，很简单

然后为了算极限相对误差，我们要算出总体估计值的标准差s，然后计算方差

我们能计算的只有样本的方差，所以最后还是用的样本的方差表示总体估计值的方差
在这里插入图片描述

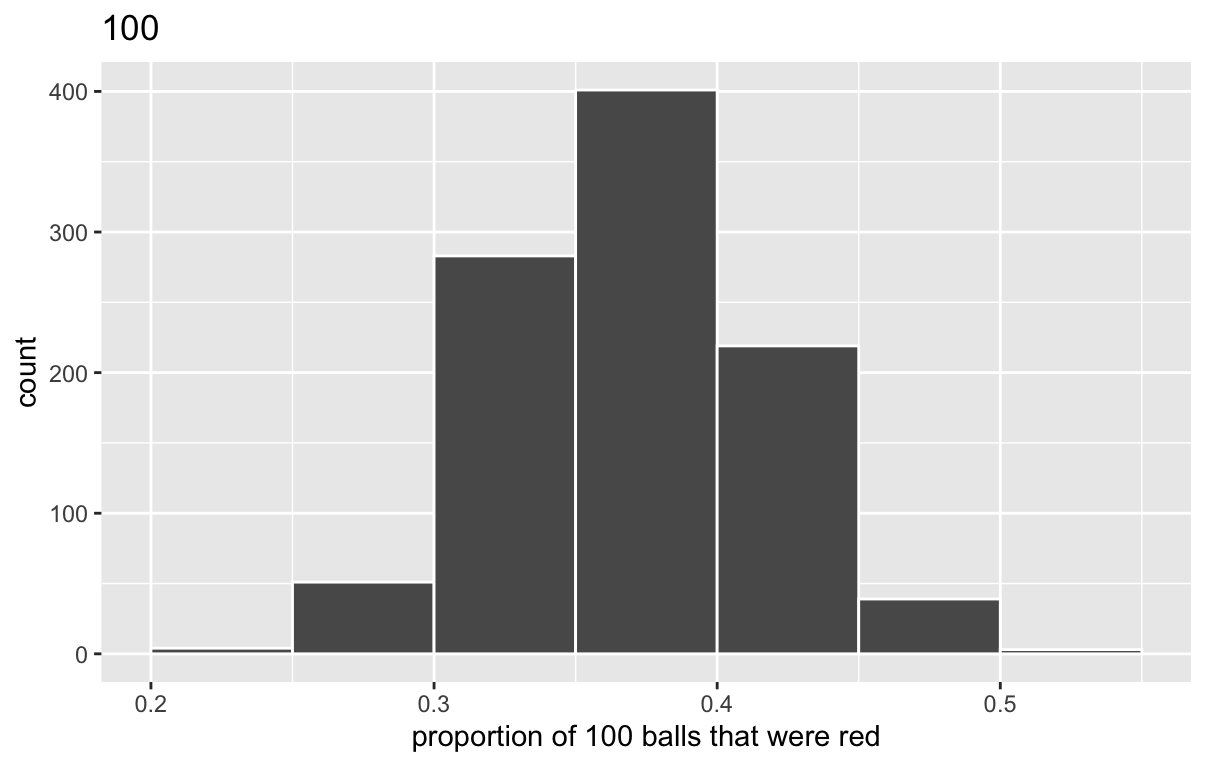
对总体比例的估计

我们要估计某一类特征的单元占总体单元数的比例P
对于一个特征A，我们先设计一个估计量Y，将总体单元分为两类
在这里插入图片描述
那么P就可以算出来了
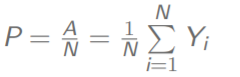
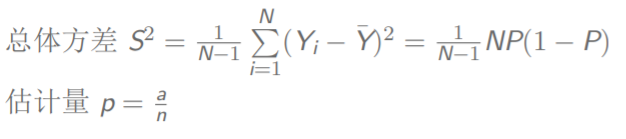
在这里插入图片描述
在这里插入图片描述
很爽的是，对于简单随机抽样，样本的p是总体的P的无偏估计

总体的方差可以这样通过样本来算出来

意思就是，如果要算总体的方差V(P)，那么只用算样本的方差v(p)就行了
在这里插入图片描述

例子

在这里插入图片描述
先嗯算一波样本的比例p，由于p是P的无偏估计，所以就得出答案了
再算一波置信区间，这个要先算p的方差
在这里插入图片描述

比率估计量及其性质

主要变量不好搞，咱就搞辅助变量

辅助变量

就是搞一个辅助变量出来
辅助变量有几个条件

  • 辅助变量要和主要变量高度相关
  • 辅助变量的总体总值要已知

比率估计量

主要变量的比率估计量有两个

  • 总体均值的比率估计量
    在这里插入图片描述
  • 总体总值的比率估计量
    在这里插入图片描述
    这句话👴看不懂，以后再说
    在这里插入图片描述

就算样本数n比较大的时候，r也不是R_hat的无偏估计，但是是近似无偏的（n比较大的时候）
在这里插入图片描述

总体均值的期望咋算

在这里插入图片描述

总体均值的方差咋算

在这里插入图片描述

总体总值的期望咋算

在这里插入图片描述

总体总值的方差咋算

在这里插入图片描述

比率估计量的方差咋算

在这里插入图片描述

Y与X的总体协方差

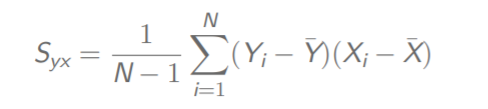
在这里插入图片描述

X的总体方差

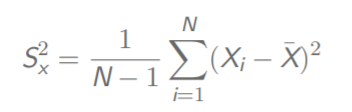
在这里插入图片描述

Y与X的总体相关系数

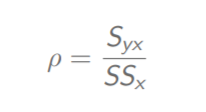
在这里插入图片描述

Y的相对方差（变异系数）

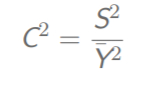
在这里插入图片描述

Y与X的相对协方差

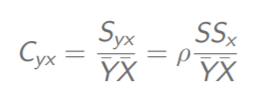
在这里插入图片描述

X的相对方差（变异系数）

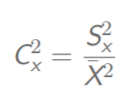
在这里插入图片描述

回归估计量及其性质

在这里插入图片描述
对于简单随机抽样，如果β为常数，则回归估计量的期望和方差如下图所示
在这里插入图片描述
既然给出了回归估计量的方程，我们可以计算出使回归估计量最小的β0
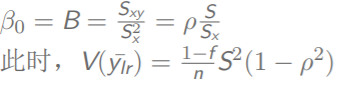
在这里插入图片描述

对于一般情况，当n足够大的时候，我们也可以这样计算回归估计量的期望和方差
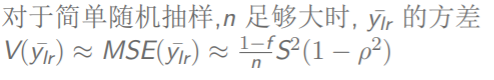
在这里插入图片描述
在这里插入图片描述

各种估计量的精度的比较

  • 当n足够大的时候
    对于以上三种估计，其方差为
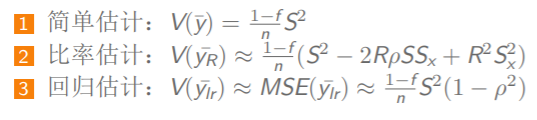
    在这里插入图片描述
    此时回归估计的结果要好于简单估计

  • 当n不够大的时候

    • 回归估计的抽样误差与比率估计相差不大
    • 回归估计的均方误差比比率估计的大，且随着n的增大而增大

简单随机抽样的实施

费用计算
在这里插入图片描述
求解抽样的样本数n
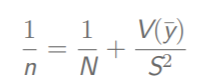
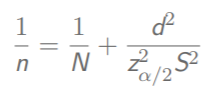
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

总体方差的估计

在这里插入图片描述

其他影响因素

在这里插入图片描述

设计效果

在这里插入图片描述


http://chatgpt.dhexx.cn/article/qBbeSZst.shtml

相关文章

R - 简单随机抽样

R - 简单随机抽样

本文使用的包 library(tidyverse) library(moderndive)使用的数据集，总共有2400个红球和白色球： bowl此处采用简单随机抽样，从2400个球中估算出红球所占比例。采用不同的抽取方法，一组是一次性抽取30个，重复1000次&a…
阅读更多...
随机抽样java_java实现从一个群体中随机抽样一定数量样本

随机抽样java_java实现从一个群体中随机抽样一定数量样本

说明 版权所有，仿冒必究 转载时请标明出处，尊重他人劳动成果，谢谢 此算法是我个人研究的，经过测试证明我的算法还是不错的。 PS：这里的时间可能有点偏小，实际用时是2秒左右，我没有去研究原因了。…
阅读更多...
ArcGIS 分类随机抽样

ArcGIS 分类随机抽样

前言 现有栅格分类图, 图中像素值代表分类编号, 取值范围为0~7。 要在每个类别中抽取100个点, 输出成带有类别的shape文件。 提取每类的随机点(流程图) 0 已有数据 一副栅格影像, 像素值代表该点的类别。 1 对类别进行循环 设置1~7的循环, 循环变量名为index。在之后的流…
阅读更多...
java随机抽样算法_随机抽样一致性（RANSAC）算法详解

java随机抽样算法_随机抽样一致性（RANSAC）算法详解

随机抽样一致性(RANSAC)算法能够有效的剔除特征匹配中的错误匹配点。 实际上，RANSAC能够有效拟合存在噪声模型下的拟合函数。实际上，RANSAC算法的核心在于将点划分为“内点”和“外点”。在一组包含“外点”的数据集中，采用不断迭代的方法&am…
阅读更多...
SPSS——随机抽样

SPSS——随机抽样

简单随机抽样 设定随机种子（Transform→Random Number Generators） 【方法一】 选择个案（Data→Select Cases） 将随机抽样的样本重新生成新的数据集，Approximately（按百分比抽样），Ex…
阅读更多...
excel如何随机抽样

excel如何随机抽样

目录 现成数据中取数——excel-数据-数据分析-抽样【方法】【案例】【步骤】【注意】 二维数据需要拍平，才能取数——利用power query【方法】【案例】【步骤】 现成数据中取数——excel-数据-数据分析-抽样 【方法】 非数值型数据：1）先生成…
阅读更多...
【抽样技术】CH2 简单随机抽样

【抽样技术】CH2 简单随机抽样

目录 前言 一、定义 二、概述 1.总体 2.单元 3.抽样比 4.样本抽取原则 5.在抽样理论中的地位与作用 三、参数估计 1.参数表示 2.对总体特征的估计思路 3.对总体均值的估计 （1）引理 （2）对总体均值的估计 4.方差和协方…
阅读更多...
Pytorch随机抽样

Pytorch随机抽样

在神经网络中，参数默认是进行随机初始化的。如果不设置的话每次训练时的初始化都是随机的，导致结果不确定。如果设置初始化，则每次初始化都是固定的。
阅读更多...
python random模块随机抽样专题

python random模块随机抽样专题

python random模块随机抽样专题 文章目录 1. 设置随机数种子 seed()2. random() 与 randint()3. sample()方法 无放回抽样4. choice() 与 choices() 有放回抽样5. shuffle()方法6. 猜拳小案例 python的random库，提供了很多随机抽样方法。             …
阅读更多...
python 有放回随机抽取_Python 随机抽样

python 有放回随机抽取_Python 随机抽样

# -*- coding: utf-8 -*- import numpy import pandas data = pandas.read_csv( D:\\PDA\\4.9\\data.csv ) #设置随机种子 numpy.random.seed(seed=2) #按照个数抽样 data.sample(n=10) #按照百分比抽样 data.sample(frac=0.02) #是否可放回抽样， #replace=True，可放回, #rep…
阅读更多...
pytorch 随机抽样

pytorch 随机抽样

情形1（按行随机排列） import torch atorch.rand(3,5) print(a) aa[torch.randperm(a.size()[0])] print(a)情形2(按列排列） aa[:,torch.randperm(a.size()[1])] print(a)结果如下 但是这里有一个问题，就是随机交换行列的顺序时…
阅读更多...
简单随机抽样

简单随机抽样

文章目录 一、安装加载扩展包二、数据描述三、简单随机抽样1. 抽样：不放回简单随机抽样抽取样本容量为300的样本（1）调用不放回简单随机抽样函数“srswor”,其中第一个参数为抽取的样本容量n,第二个参数为总体容量N。（2&#xff09…
阅读更多...
加权随机抽样算法

加权随机抽样算法

1. 基于均匀分布概率的算法 例如，3等奖抽中的概率是70%，2等奖是20%，1等奖是10%，这样，大部分人都只能中3等奖，小部分人是二等奖，而只有特别少的人才可能拿到一等奖。产生0-100之间的均匀分布的随…
阅读更多...
SPSS如何进行随机抽样

SPSS如何进行随机抽样

在统计学中，随机抽样是非常重要的一种统计分析手段，它使得研究对象有相同的机会被分在某一处理组当中，排除人为因素的影响和干扰。随机抽样是提高研究样本代表性和组间均衡性的重要方法，它的正确使用将直接影响到研究成果的可靠性…
阅读更多...
linux内核编程memcpy,Linux库memcpy函数实现

linux内核编程memcpy,Linux库memcpy函数实现

memcpy函数在面试中很容易被问到如何去实现。memcpy函数是内存拷贝函数，用于将一段内存空间数据拷贝到另一段内存空间中，但是它和memmove函数不同的是，它对内存空间有要求的，dest和src所指向的内存空间不能重叠，否则的…
阅读更多...
memcpy函数及其缺陷分析

memcpy函数及其缺陷分析

函数介绍 函数原型 void *memcpy(void *destin, void *source, unsigned n); 参数 destin-- 指向用于存储复制内容的目标数组，类型强制转换为 void* 指针。 source-- 指向要复制的数据源，类型强制转换为 void* 指针。 n-- 要被复制的字节数。 返回值…
阅读更多...
memcpy函数优化及DMA对比

memcpy函数优化及DMA对比

一、背景与目的 优化算法结构，提高芯片的使用效率，挖掘芯片的潜在能力，对提高产品质量，降低产品成本有着重要意义，在性能受限的嵌入式设备更加重要。 在使用C语言编程时，我们常用memcpy来复制内存数据&…
阅读更多...
memcpy函数的介绍以及实现

memcpy函数的介绍以及实现

一、memcpy函数的介绍 memcpy函数在C语言的作用是将第一个变量a中的前num个字节的变量替换成第二个变量b的前num个字节 memcpy - C Reference (cplusplus.com) 二、memcpy函数的模拟实现 我的思路是这样的：首先，要判断这两个传来的地址是否是空指针&…
阅读更多...
Linux下的memcpy函数

Linux下的memcpy函数

之前写过一篇关于 memcpy函数面试的文章 几个简单的笔试题 里面的代码使用的是char指针来实现，今天我们来看看Linux下面的memcpy 函数，它的实现上还是有一些巧妙的。 void * memcpy(void * dest, const void *src, size_t n) {if (!(((unsigned long) de…
阅读更多...
内存操作函数:memcpy函数，memove函数

内存操作函数:memcpy函数，memove函数

目录: 1.memcpy函数(内存拷贝)(1)memcpy函数的说明(2)memcpy的使用a.代码b.结果 (3)memcpy的模拟实现a.代码b.结果 2.memmove函数(1)memmove函数的说明(2)内存重叠问题a.分析b.代码说明 (3)内存重叠问题的解决分析(4)memmove的使用(5)模拟实现memmove 1.memcpy函数(内存拷贝) …
阅读更多...
推荐文章

Copyright @ 2022~2023