目录
- 1 Learing to Rank介绍
- 2 The Pointwise Approach
- 3 The Pairwise Approach
- 3.1 RankNet
- 4 The Listwise Approach
- 4.1 直接优化评测指标
- 4.1.1 LambdaRank
- 4.1.2 LambdaMART
- 4.2 定义Listwise损失函数
- 4.2.1 ListNet
- 4.2.2 ListMLE
- 5 排序评估指标
- 5.1 Mean Reciprocal Rank (MRR)
- 5.2 Mean Average Precision (MAP)
- 5.3 Normalized Discounted Cumulative Gain (NDCG)
- 5.4 Rank Correlation (RC)
- 6 参考
1 Learing to Rank介绍
Learning to Rank (LTR)是一类技术方法,主要利用机器学习算法解决实际中的排序问题。传统的机器学习主要解决的问题是一个分类或者回归问题,比如对一个样本数据预测对应的类别或者预测一个数值分值。而LTR解决的是一个排序问题,对一个list的item进行一个排序,所以LTR并不太关注这个list的每个item具体得多少分值,更关注所有item的相对顺序。排序通常是信息检索的核心成分,所以LTR最常见的应用是搜索场景,对召回的document进行排序。对于排序算法从训练方式来看,主要分为三类:pointwise,pairwise和listwise方式,接下来对这三种方法进行介绍。
2 The Pointwise Approach
pointwise方法损失函数计算只与单个document有关,本质上是训练一个分类模型或者回归模型,判断这个document与当前的这个query相关程度,最后的排序结果就是从模型对这些document的预测的分值进行一个排序。对于pointwise方法,给定一个query的document list,对于每个document的预测与其它document是独立的。所以模型输入和对应的标签label形式如下:
- 输入: 单个document
- 标签label: document所属类型或者分值
pointwise方法将排序任务看做对单个文本的回归或者分类任务来做。若文档document的相关性等级有K种,则我们可以建模为一个有K个类别的 { 0 , 1 , 2 , . . . , K − 1 } \{0,1,2,..., K-1\} {0,1,2,...,K−1}的Multi-class分类任务,则 y i ∈ R k y_i \in \R^k yi∈Rk是一个k维度的one-hot表示, 我们可以用交叉熵loss作为目标损失函数:
L = − ( y i log ( p i ) − ( 1 − y i ) log ( 1 − p i ) ] ) L = -(y_i\log(p_i) - (1-y_i)\log(1-p_i)]) L=−(yilog(pi)−(1−yi)log(1−pi)])
3 The Pairwise Approach
基于pairwise的方法,在计算目标损失函数的时候,每一次需要基于一个pair的document的预测结果进行损失函数的计算。比如给定一个pair对的document,优化器需要优化的是两个document的排序关系,与groud truth的排序顺序保持一致。目标是最小化与groud truth不一致的排序对。在实际应用中,pairwise方法比pointwise效果更好,因为预测相对的排序相比预测一个类别或者一个分值,更符合排序的性质。其中模型输入和对应的标签label形式如下:
- 输入: 一个pair对document (A,B)
- 输出标签: 相对顺序label (1, 0.5, 0)
其中1表示相关性等级A>B,0.5表示相关性等级A=B,0表示相关性等级A<B。目前使用较多的pairwise排序算法有RankNet,接下来对这种算法原理进行介绍。
3.1 RankNet
RankNet将排序问题转成对候选集所有document的pair对的分类问题,对query的document list分成两两pair对,并且根据每个文本的相关性等级,确定pair对的标签label, 如下图所示:

模型训练的任务是,判断两两pair之间的相关性相对大小。根据pair对的相关性等级大小,我们可以得到训练过程中每个pair对的标签label:
P i j ‾ = { 1 文 本 的 相 关 性 等 级 r i > r j 1 2 文 本 的 相 关 性 等 级 r i = r j 0 文 本 的 相 关 性 等 级 r i < r j \overline{P_{ij}}=\begin{cases} 1\quad 文本的相关性等级r_i>r_j \\ \frac{1}{2} \quad 文本的相关性等级r_i=r_j \\ 0 \quad 文本的相关性等级r_i<r_j \end{cases} Pij=⎩⎪⎨⎪⎧1文本的相关性等级ri>rj21文本的相关性等级ri=rj0文本的相关性等级ri<rj
其中:
P i j ‾ = 1 2 ( 1 + S i j ) ( 1 ) \overline{P_{ij}}=\frac{1}{2}(1+S_{ij}) \text{ } \text{ } \text{ } \text{ }(1) Pij=21(1+Sij) (1)
S i j ∈ { 0 , + 1 , − 1 } S_{ij} \in \{0, +1, -1\} Sij∈{0,+1,−1},对于给定一个query,若文本 i i i的相关性比文本 j j j高,则 S i j S_{ij} Sij=1, 若文本 i i i的相关性比文本 j j j高,则 S i j S_{ij} Sij=-1,文本 i i i的相关性与文本 j j j相等,则 S i j S_{ij} Sij=0。
而每个pair对模型预测的概率分值计算如下:
P i j = 1 1 + e − σ ⋅ ( s i − s j ) ( 2 ) P_{ij} =\frac{1}{1+e^{-\sigma \cdot (s_i-s_j)}} \text{ } \text{ } (2) Pij=1+e−σ⋅(si−sj)1 (2)
参数 σ \sigma σ决定了sigmoid函数的形状,其中 s i s_i si表示的是第 i i i个document经过模型得到的预测分值。可以看出若 s i − s j s_i-s_j si−sj越大,则 P i j P_{ij} Pij也越接近1,与pair对的标签 P i j ‾ = 1 \overline{P_{ij}}=1 Pij=1越符合。对于pair对,我们同样可以用交叉熵loss作为目标损失函数如下:
L = − P i j ‾ log ( P i j ) − ( 1 − P i j ‾ ) log ( 1 − P i j ) ( 3 ) L = -\overline{P_{ij}}\log(P_{ij}) - (1 - \overline{P_{ij}})\log(1-P_{ij}) \text{ } \text{ } (3) L=−Pijlog(Pij)−(1−Pij)log(1−Pij) (3)
通过Stochastic Gradient Descent随机梯度下降算法就可以优化求解模型参数权重了。在预测的阶段,对输入的是每个document得到模型预测分值 s i s_i si,根据document对应的分值就可进行排序结果。有人基于FRank对目标损失函数进行一个改进,试验效果取得了更好的结果,新定义的损失函数如下:
L = 1 − ( P i j ‾ ⋅ P i j + ( 1 − P i j ‾ ) ⋅ ( 1 − P i j ) ) L = 1 - (\sqrt{\overline{P_{ij}}\cdot P_{ij}} + \sqrt{(1-\overline{P_{ij}}) \cdot (1 - P_{ij})}) L=1−(Pij⋅Pij+(1−Pij)⋅(1−Pij))
如下是loss的函数图像对比情况:

基于pairwise的排序算法后面还有很多工作进行了改进,并取得了不错的效果,在这里就不一一介绍了。pairwise相对pointwise,不再假设绝对的相关性,而是有了相对的关系,但是排序的性质还没有完全在模型里得到体现。比如,如下两组排序,从pairwise来看,准确率是一致的,但是从整个排序效果来看,第二组是比第一组排序效果好的:
| 说明 | 理想的排序结果 | 第一组排序结果 | 第二组排序结果 |
|---|---|---|---|
| (p: perfec), (g: good), (b: bad) | p g g b b b b | g p g b b b b | p g b g b b b |
4 The Listwise Approach
Listwise方法是直接对整个list的document的排序进行优化,目标损失函数中优化整个list的document的排序结果。所以训练样本的输入和标签label输出结果如下:
- 输入: 整个list document
- 标签label: 排序好的document list
目前主要有两种方法来做listwise排序:
- 直接优化信息检索的测量指标:比如NDCG,这类型的算法主要由SoftRank, AdaRank等
- 最小化损失函数: 计算整个list的loss,最小化损失函数,比如ListNet,ListMLE等
4.1 直接优化评测指标
通过直接优化排序结果中的评测指标来优化排序任务,但是基于评测指标比如NDCG依赖排序结果,是不连续不可导的。所以优化这些不连续不可导的目标函数面临较大的挑战,目前多数优化技术都是基于函数可导的情况。那么如何解决这个问题?常见的有如下两种方法:
- 通过使用优化技术将目标函数转变成连续可导的函数,然后进行求解,比如SoftRank和 AdaRank等模型
- 通过使用优化技术对非连续的不可导目标函数就行求解,比如 LambdaRank
4.1.1 LambdaRank
LambadRank
上面介绍了RankNet的原理,RankNet优化目标是最小化pair对错误,但是在信息检索领域比如NDCG这样的评测指标,这样的优化目标并不能够最大化效果,通常在信息检索中我们更关注的是topN的排序结果,且相关性越大的文本最需要排在最前面。如下图所示:
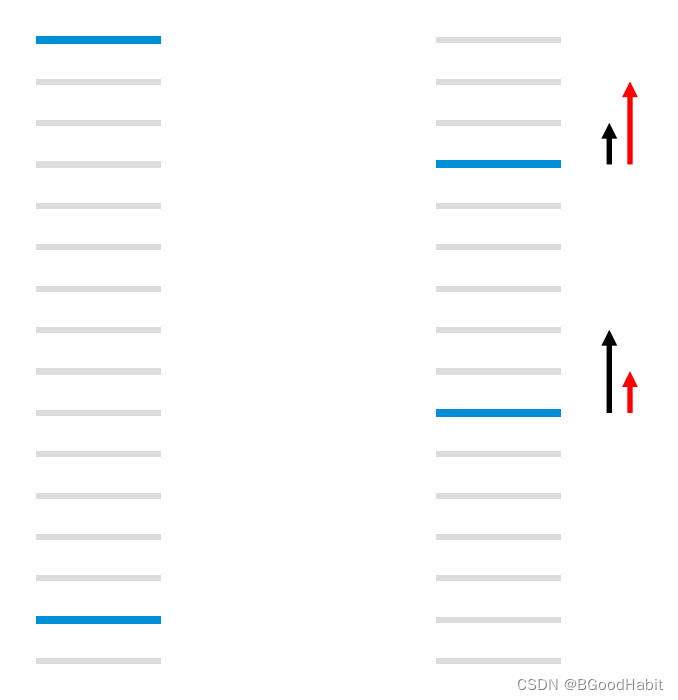
给定一个query,上图为排序结果展示,其中蓝色的线表示的是相关的文档,灰色的线表示不相关的文档,那么在左图,有13个pair对错误,而在右图中,有11个pair对错误,在RankNet,右图的排序结果要比左图好,但是在信息检索指标中,比如NDCG指标,左图的效果比右边更好。
我们在上面介绍RankNet中,将上述(1)(2)公式代人到(3)公式中,我们可以得到损失函数如下:
C = 1 2 ( 1 − S i j ) σ ( s i − s j ) + l o g ( 1 + e − σ ( s i − s j ) ) ( 4 ) C =\frac{1}{2}(1-S_{ij})\sigma(s_i-s_j)+log(1+e^{-\sigma(s_i-s_j)}) \text{ }\text{ }(4) C=21(1−Sij)σ(si−sj)+log(1+e−σ(si−sj)) (4)
从上面公式可以得出,当 S i j = 1 S_{ij}=1 Sij=1, 则损失函数变为如下:
C = l o g ( 1 + e − σ ( s i − s j ) ) ( 5 ) C = log(1+e^{-\sigma(s_i-s_j)}) \text{ }\text{ }(5) C=log(1+e−σ(si−sj)) (5)
要使得C变小,则 s i s_i si大于 s j s_j sj且差距越大,C越小,与该pair对的相对相关性强度标签label S i j = 1 S_{ij}=1 Sij=1(文本i比文本j更相关,也就是 s i > s j s_i>s_j si>sj)保持一致。
而当 S i j = − 1 S_{ij}=-1 Sij=−1,则代价函数如下:
C = l o g ( 1 + e − σ ( s j − s i ) ) ( 6 ) C=log(1+e^{-\sigma(s_j-s_i)}) \text{ }\text{ }(6) C=log(1+e−σ(sj−si)) (6)
同理, s j > s i s_j>s_i sj>si差距越大,损失函数C越小,与该pair对的相对相关性强度标签label S i j = − 1 S_{ij}=-1 Sij=−1(文本j比文本i更相关,也就是 s j > s i s_j>s_i sj>si)保持一致。
我们来计算下损失函数对 s i s_i si求导:
∂ C ∂ s i = σ ( 1 2 ( 1 − S i j ) − 1 1 + e σ ( s i − s j ) ) = − ∂ C ∂ s j \frac{\partial C}{\partial s_i}=\sigma(\frac{1}{2}(1-S_{ij}) - \frac{1}{1+e^{\sigma(s_i-s_j)}})=-\frac{\partial C}{\partial s_j} ∂si∂C=σ(21(1−Sij)−1+eσ(si−sj)1)=−∂sj∂C
那么损失函数对模型参数 w k w_k wk的导数计算如下:
∂ C ∂ w k = ∂ C ∂ s i ∂ s i ∂ w k + ∂ C ∂ s j ∂ s j ∂ w k \frac{\partial C}{\partial w_k} =\frac{\partial C}{\partial s_i}\frac{\partial s_i}{\partial w_k}+\frac{\partial C}{\partial s_j}\frac{\partial s_j}{\partial w_k} ∂wk∂C=∂si∂C∂wk∂si+∂sj∂C∂wk∂sj
= σ ( 1 2 ( 1 − S i j ) − 1 1 + e σ ( s i − s j ) ) ( ∂ s i ∂ w k − ∂ s j ∂ w k ) =\sigma(\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{\sigma(s_i-s_j)}})(\frac{\partial s_i}{\partial w_k} - \frac{\partial s_j}{\partial w_k}) =σ(21(1−Sij)−1+eσ(si−sj)1)(∂wk∂si−∂wk∂sj)
我们定义:
λ i j = ∂ C ( s i − s j ) ∂ s i = σ ( 1 2 ( 1 − S i j ) − 1 1 + e σ ( s i − s j ) ) ( 7 ) \lambda_{ij}=\frac{\partial C(s_i-s_j)}{\partial s_i}=\sigma(\frac{1}{2}(1-S_{ij}) - \frac{1}{1+e^{\sigma(s_i-s_j)}}) \text{ }\text{ }(7) λij=∂si∂C(si−sj)=σ(21(1−Sij)−1+eσ(si−sj)1) (7)
对于一个给定的query,我们定义 I I I表示所有pair对的索引 { i , j } \{i,j\} {i,j},其中文本 U i U_i Ui的相关性大于 U j U_j Uj,也就是说 S i j = 1 S_{ij}=1 Sij=1,则上面的公式转变形式为:
λ i j = − σ 1 + e ( s i − s j ) < 0 ( 8 ) \lambda_{ij}=-\frac{\sigma}{1+e^{(s_i -s_j)}} <0 \text{ }\text{ }(8) λij=−1+e(si−sj)σ<0 (8)
因为 λ i j < 0 \lambda_{ij} <0 λij<0,则由于这个pair对产生的梯度更新 s i − λ i j > s i s_i-\lambda_{ij}>s_i si−λij>si, s i s_i si是增加的,也就是若 U i > U j U_i >U_j Ui>Uj,模型的每次调整需要调高 s i s_i si的预测值,但是对于另外一些pair对(j, i) , U j > U i U_j>U_i Uj>Ui,对于这样的pair对,更新梯度后,需要调低 s i s_i si的分值。所以综合所有的pair对情况,对于文本 U i U_i Ui我们计算梯度 λ i \lambda_i λi公式如下:
λ i = ∑ j : { i , j } ∈ I λ i j − ∑ j : { j , i } ∈ I λ i j ( 9 ) \lambda_i = \sum_{j:\{i,j\} \in I} \lambda_{ij} - \sum_{j:\{j,i\}\in I} \lambda_{ij} \text{ }\text{ } (9) λi=j:{i,j}∈I∑λij−j:{j,i}∈I∑λij (9)
对于所有的pair对,那些 { i , j } ∈ I \{i,j\} \in I {i,j}∈I需要调高 s i s_i si,而那些 { k , i } ∈ I \{k,i\} \in I {k,i}∈I的则需要调低 s i s_i si,最后,综合所有pair对,由上述公式(8)决定梯度值 λ i \lambda_i λi是小于0还是大于0,决定是调高 s i s_i si值还是调低 s i s_i si的值。RankNet就是由所有pair对错误情况去调整每个文本的 U i U_i Ui的排序位置,但是并不很适合信息检索类似NDCG这样的指标。
所以在LambdaRank算法里,定义的梯度 λ i j \lambda_{ij} λij公式如下:
λ i j = ∂ C ( s i − s j ) ∂ s i = − σ 1 + e σ ( s i − s j ) ∣ Δ N D C G ∣ ( 10 ) \lambda_{ij} = \frac{\partial C(s_i - s_j)}{\partial s_i}=\frac{-\sigma}{1+e^{\sigma^{(s_i -s_j)}}}|\Delta NDCG| \text{ }\text{ } (10) λij=∂si∂C(si−sj)=1+eσ(si−sj)−σ∣ΔNDCG∣ (10)
在公式(8)的基础上再乘以 ∣ Δ N D C G ∣ |\Delta NDCG| ∣ΔNDCG∣,而 ∣ Δ N D C G ∣ |\Delta NDCG| ∣ΔNDCG∣表示的是交换 U i U_i Ui和 U j U_j Uj两个文本 (其它文本保持不变)后对应的NDCG分数的变化。
为什么要乘以这个变化后的 ∣ Δ N D C G ∣ |\Delta NDCG| ∣ΔNDCG∣?
λ i \lambda_{i} λi代表了文档 U i U_i Ui下一次优化是提升还是下降,对于RankNet,根据pair对的错误数量决定调整,但是lambdarank还要考虑pair对的重要性(用变化后的NDCG表示),pair对(i,j)交换位置后,对应的 ∣ Δ N D C G ∣ |\Delta NDCG| ∣ΔNDCG∣若变化很大,那说明 U i U_i Ui是个很重要的文本,这个pair对的 λ i j \lambda_{ij} λij起到的作用要增大,所以我们可以理解用 ∣ Δ N D C G ∣ |\Delta NDCG| ∣ΔNDCG∣代表这个 λ i j \lambda_{ij} λij权重,防止对重要文本下调。
4.1.2 LambdaMART
LambdaMART是Lambda和MART(Multiple Additive Regression Tree)组成,上面部分我们介绍了Lambda,根据导数公式(10)可知,损失函数C定义如下:
C = ∑ { i , j } ∣ Δ Z i j ∣ l o g ( 1 + e − σ ( s i − s j ) ) C=\sum_{\{i,j\}}|\Delta Z_{ij}|log(1+e^{-\sigma(s_i-s_j)}) C={i,j}∑∣ΔZij∣log(1+e−σ(si−sj))
这里的 ∣ Δ Z i j ∣ |\Delta Z_{ij}| ∣ΔZij∣表示的信息检索指标,比如NDCG等。损失函数的一阶导数为:
∂ C ∂ s i = ∑ { i , j } − σ ∣ Δ Z i j ∣ 1 + e σ ( s i − s j ) = ∑ i , j − σ ∣ Δ Z i j ∣ p i j \frac{\partial C}{\partial s_i} = \sum_{\{i,j\}} \frac{-\sigma |\Delta Z_{ij}|}{1+e^{\sigma(s_i-s_j)}}=\sum_{i,j}-\sigma|\Delta Z_{ij}|p_{ij} ∂si∂C={i,j}∑1+eσ(si−sj)−σ∣ΔZij∣=i,j∑−σ∣ΔZij∣pij
我们定义:
p i j = 1 1 + e σ ( s i − s j ) = − λ i j σ ∣ Z i j ∣ p_{ij}=\frac{1}{1+e^{\sigma(s_i-s_j)}}=\frac{-\lambda_{ij}}{\sigma|Z_{ij}|} pij=1+eσ(si−sj)1=σ∣Zij∣−λij
那么二阶导数为:
∂ 2 C ∂ s i 2 = ∑ { i , j } σ 2 ∣ Δ Z i j ∣ p i j ( 1 − p i j ) \frac{\partial^2C}{\partial s_i^2} = \sum_{\{i,j\}} \sigma^2|\Delta Z_{ij}|p_{ij}(1-p_{ij}) ∂si2∂2C={i,j}∑σ2∣ΔZij∣pij(1−pij)
LambdaMART模型是由许多棵决策树,通过Boosting思想组成,每颗决策树拟合的是损失函数的梯度,其中叶子节点的权重 w w w具体求解涉及一阶梯度和二阶梯度,大家可以先了解GBDT算法原理讲解,对一些基本原理进行熟悉。而在这里求解的梯度用lambda方式求解。LambdaMART算法求解步骤如下:
 可以看出这里求解一阶和二阶导数用lambda替代,算法的逻辑和求解boosting算法逻辑一致。
可以看出这里求解一阶和二阶导数用lambda替代,算法的逻辑和求解boosting算法逻辑一致。
4.2 定义Listwise损失函数
4.2.1 ListNet
ListNet与RankNet很相似,RankNet是用pair对文本排序顺序进行模型训练,而ListNet用的是整个list文本排序顺序进行模型训练。若训练样本中有m个query,假如对应需要排序的最多文本数量为n ,则RankNet的复杂度为 O ( m ⋅ n 2 ) O(m \cdot n^2) O(m⋅n2),而ListNet的复杂度为 O ( m ⋅ n ) O(m \cdot n) O(m⋅n),所以整体来说在训练过程中ListNet相比RankNet更高效。
假设对于query q i q^i qi对应排序的文本为:
d i = ( d 1 i , d 2 i , d 3 i , . . . , d n i ) d^i=(d_1^i, d_2^i, d_3^i, ...,d^i_n) di=(d1i,d2i,d3i,...,dni)
其中对应的特征为:
x i = ( x 1 i , x 2 i , x 3 i , . . . , x n i ) x^i = (x^i_1, x_2^i, x_3^i, ..., x_n^i) xi=(x1i,x2i,x3i,...,xni)
假设我们用神经网络模型作为基础的分值预测,那么对每个样本的特征输入,模型都会给出预测分值:
z i = ( f ( x 1 i ) , f ( x 2 i ) , . . . , f ( x n i ) ) z^i = (f(x_1^i), f(x_2^i), ..., f(x_n^i)) zi=(f(x1i),f(x2i),...,f(xni))
对于每个文本的实际分值记录为:
y i = ( y 1 i , y 2 i , . . . , f n i ) y^i = (y_1^i, y_2^i, ...,f_n^i) yi=(y1i,y2i,...,fni)
则我们可以定义损失函数为:
∑ i = 1 m L ( y i , z i ) \sum_{i=1}^m L(y^i, z^i) i=1∑mL(yi,zi)
这里的L我们可以用交叉熵损失函数定义,度量两个分布 y i , z i y^i, z^i yi,zi之间的差异:
L ( y i , z i ( f w ) ) = − ∑ j = 1 n P y i ( x j i ) l o g ( P z i ( f w ) ( x j i ) ) L(y^i, z^i(f_w)) = -\sum_{j=1}^n P_{y^i}(x_j^i)log(P_{z^i(f_w)}(x_j^i)) L(yi,zi(fw))=−j=1∑nPyi(xji)log(Pzi(fw)(xji))
其中 P y i ( x j i ) P_{y^i}(x_j^i) Pyi(xji)表示的对于给定query i i i,对应第 j j j个文本输入特征为 x j i x^i_j xji对应的概率值,这个概率值我们可以根据每个文档的等级分值,经过一个softmax函数求出概率值,比如,对应的文本相关性等级为:
y i = { 5 , 4 , 3 , 1 } y^i=\{5, 4, 3, 1\} yi={5,4,3,1}
则第一个文本等级为5对应的概率分值为:
P ( x 1 i ) = e 5 e 5 + e 4 + e 3 + e 1 P(x_1^i)=\frac{e^5}{e^5+e^4+e^3+e^1} P(x1i)=e5+e4+e3+e1e5
而经过神经网络 f w f_w fw,每个文本对应的概率分值也是经过一个softmax函数求得:
P z i ( f w ) ( x j i ) = exp ( f w ( x j i ) ) ∑ k = 1 n exp ( f w ( x k i ) ) P_{z^i(f_w)(x_j^i)} = \frac{\exp(f_w(x_j^i))}{\sum_{k=1}^n \exp(f_w(x_k^i)) } Pzi(fw)(xji)=∑k=1nexp(fw(xki))exp(fw(xji))
这样我们就可以用交叉熵损失函数度量两个分布之间的差异,计算出loss,然后用梯度下降算法求解。
4.2.2 ListMLE
ListMLE也是基于list计算损失函数,论文对learning to rank算法从函数凸性,连续性,鲁棒性等多个维度进行了分析,提出了一种基于最大似然loss的listwise排序算法,取名为ListMLE。损失函数定义如下:
L ( g ( x ) , y ) = − l o g P ( y ∣ x ; g ) L(g(x),y) = -logP(y|x;g) L(g(x),y)=−logP(y∣x;g)
其中 P ( y ∣ x ; g ) P(y|x;g) P(y∣x;g)概率计算如下:
P ( y ∣ x ; g ) = ∏ i = 1 n exp ( g ( x y ( i ) ) ) ∑ k = i n exp ( g ( x y ( k ) ) ) P(y|x;g) = \prod_{i=1}^n \frac{\exp(g(x_{y(i)}))}{\sum_{k=i}^n\exp(g(x_{y(k)}))} P(y∣x;g)=i=1∏n∑k=inexp(g(xy(k)))exp(g(xy(i)))
我们用一个具体的例子来说明上述公式,假如对给定的query,其中对应的文本相关性等级为:
D = [ 3 , 5 , 1 , 2 ] D=[3, 5, 1, 2] D=[3,5,1,2]
模型预测的logit分值对应为:
p r e d = [ 2.2 , 3.1 , 1.8 ] pred=[2.2, 3.1, 1.8] pred=[2.2,3.1,1.8]
按照D的相关性文本大小对应模型预测的分值顺序调整后为:
p r e d s = [ 3.1 , 2.2 , 1.8 ] pred^s=[3.1,2.2,1.8] preds=[3.1,2.2,1.8]
则对应的概率分值为:
P = 3.1 3.1 + 2.2 + 1.8 × 2.2 2.2 + 1.8 × 1.8 1.8 P = \frac{3.1}{3.1+2.2+1.8} \times \frac{2.2}{2.2+1.8}\times \frac{1.8}{1.8} P=3.1+2.2+1.83.1×2.2+1.82.2×1.81.8
对应的最大似然loss为:
l o s s = − log ( P ) loss = -\log(P) loss=−log(P)
5 排序评估指标
在排序任务中,模型对候选集进行打分,得到一个排序结果,再与真实的排序结果进行对比,通过一些指标来衡量排序模型的预测效果。而用的较广泛的评判标注主要分三部分:
- Binary judgment: 判断query与document相关与不相关,两种结果
- Multi-level ratings: 分perfect >excellent > good >fair > bad 5种相关性等级
- pairwise preferences: 给定一个query的两个document A, B,判断A与B谁相对query更相关
那么如何衡量排序模型的效果呢?接下来会对测评指标进行简单的介绍。
5.1 Mean Reciprocal Rank (MRR)
对于给定query q q q以及与该query相关的文本 D = { d 1 , d 2 , d 3 , d 4 , d 5 } D=\{d_1,d_2,d_3,d_4,d_5\} D={d1,d2,d3,d4,d5},假设文本与query的相关性程度依次递减已经排好序,若排序模型预测的顺序是 r a n k = { d 2 , d 3 , d 1 , d 5 , d 4 } rank=\{d_2,d_3,d_1,d_5,d_4\} rank={d2,d3,d1,d5,d4},则与该query第一相关的文本 d 1 d_1 d1所在的排序位置记为 r ( q ) = 3 r(q)=3 r(q)=3,则对于这个query的MRR指标计算结果为:
MRR = 1 r ( q ) = 1 3 \text{MRR} = \frac{1}{r(q)} =\frac{1}{3} MRR=r(q)1=31
该指标对应的值越大越好,且取值范围为 [ 1 N , 1 ] [\frac{1}{N},1] [N1,1],其中 N N N表示的是排序的总文本数量。
5.2 Mean Average Precision (MAP)
MAP是排序模型效果评估的另外一个评价指标,首先我们定义在位置 k k k的精确率记为: P @ k P@k P@k,具体计算结果为:
P @ k ( q ) = # { relevant documents in the top k positions } k P@k(q) = \frac{\#\{\text{relevant documents in the top k positions}\}}{k} P@k(q)=k#{relevant documents in the top k positions}
则平均精确率AP定义如下:
A P ( q ) = ∑ k = 1 m P @ k ( q ) ⋅ l k # { relevant documents} AP(q) = \frac{\sum_{k=1}^m P@k(q) \cdot l_k}{\#\{\text{relevant documents\}}} AP(q)=#{relevant documents}∑k=1mP@k(q)⋅lk
其中 m m m表示的是query q q q对应的所有文本数量, l k l_k lk取值为{0,1},判断在第 k k k个位置上的文本是否与query相关,相关为1,不相关为0。假设query对应排序的有5个document,其中红色代表不相关,绿色代表相关,则AP指标计算结果为:

A P = 1 3 ⋅ ( 1 1 + 2 3 + 3 5 ) AP = \frac{1}{3} \cdot(\frac{1}{1} + \frac{2}{3} + \frac{3}{5}) AP=31⋅(11+32+53)
则最后的MAP指标表示所有query的平均AP值:
MAP = 1 m ∑ i m A P ( q i ) \text{MAP} = \frac{1}{m}\sum_i^m AP(q_i) MAP=m1i∑mAP(qi)
5.3 Normalized Discounted Cumulative Gain (NDCG)
前面的测量标准主要基于是否相关的0-1 binary决策,而DCG可以对包含多个相关性程度的类别进行测评,同时将位置衰减因子也定义到了计算公式里,假设对于query q q q,排序模型预测的相关性结果从高到低排序后记为 π \pi π,则在位置k的DCG指标定义如下:
D C G @ k ( q ) = ∑ r = 1 k G ( π ( r ) ) η ( r ) DCG@k(q) = \sum_{r=1}^kG(\pi(r))\eta(r) DCG@k(q)=r=1∑kG(π(r))η(r)
其中 π ( r ) \pi(r) π(r)表示的是排序 π \pi π整个list在位置为 r r r的原始文档相关性等级, G ( ⋅ ) G(\cdot) G(⋅)是对文档相关性计算出的新的等级分值,一般计算函数如下:
G ( π ( r ) ) = 2 π ( r ) − 1 G(\pi(r)) = 2^{\pi(r)} -1 G(π(r))=2π(r)−1
其中 η ( r ) \eta(r) η(r)表示的是位置衰减因子,通常计算公式如下:
η ( r ) = 1 log 2 ( r + 1 ) \eta(r) = \frac{1}{\log_2(r+1)} η(r)=log2(r+1)1
所以从DCG公式可以看出,若相关性等级越高的文档排序越靠后,则由于 η ( r ) 位 置 衰 弱 的 越 大 , \eta(r)位置衰弱的越大, η(r)位置衰弱的越大,DCG分值越低,且将位置信息融入到了计算公式里。则归一化的Normalized DCG (NDCG) 指标计算公式如下:
N D C G @ k ( q ) = 1 Z k ∑ r = 1 k G ( π ( r ) ) η ( r ) = ∑ r = 1 k ( 2 π ( r ) − 1 ) ⋅ ( 1 / log 2 ( r + 1 ) ) Z k NDCG@k(q) = \frac{1}{Z_k}\sum_{r=1}^kG(\pi(r))\eta(r) = \frac{ \sum_{r=1}^k (2^{\pi(r)} -1)\cdot(1/\log_2(r+1))}{Z_k} NDCG@k(q)=Zk1r=1∑kG(π(r))η(r)=Zk∑r=1k(2π(r)−1)⋅(1/log2(r+1))
其中 Z k Z_k Zk是归一化因子,其计算值为DCG@k的最大值,也就是query对应的理想排序list (相关性等级越高,排在越靠前),可以看出NDCG@k(q)计算公式由4部分组成:归一化因子 Z k Z_k Zk, 累积求和: ∑ r = 1 k \sum_{r=1}^k ∑r=1k,信息增益Gain: ( 2 π ( r ) − 1 ) (2^{\pi(r)} -1) (2π(r)−1)以及位置衰减: 1 / log 2 ( r + 1 ) ) 1/\log_2(r+1)) 1/log2(r+1)), NDCG的取值范围为[0,1]。若根据Relevance Rating进行打标,则信息增益Gain值如下:
| Relevance Rating | Value (Gain) |
|---|---|
| Perfect | 31 = 2 5 − 1 31=2^5-1 31=25−1 |
| Excellent | 15 = 2 4 − 1 15=2^4-1 15=24−1 |
| Good | 7 = 2 3 − 1 7=2^3-1 7=23−1 |
| Fair | 3 = 2 2 − 1 3=2^2-1 3=22−1 |
| Bad | 0 = 2 0 − 1 0=2^0-1 0=20−1 |
5.4 Rank Correlation (RC)
RC指标是衡量模型预测的一个排序list π \pi π与groudtruth标准排序list π l \pi_l πl之间的相关性。用带权重的Kendall等级相关系数作为评估准则,评估两个排序list中两两不一样的pairwise排序一致性情况,计算公式定义如下:
R C = ∑ u < v w u , v ( 1 + s g n ( ( π ( u ) − π ( v ) ) ( π l ( u ) − π l ( v ) ) ) ) 2 ∑ u < v w u , v RC = \frac{\sum_{u<v}w_{u,v}(1+sgn((\pi(u) - \pi(v))(\pi_l(u) - \pi_l(v))))}{2\sum_{u<v}w_{u,v}} RC=2∑u<vwu,v∑u<vwu,v(1+sgn((π(u)−π(v))(πl(u)−πl(v))))
其中sgn是符合函数,定义如下:
s g n = { 1 x > 0 0 x = 0 − 1 x < 0 sgn=\begin{cases} 1\quad x>0 \\ 0 \quad x=0 \\ -1 \quad x<0 \end{cases} sgn=⎩⎪⎨⎪⎧1x>00x=0−1x<0
从上述公式可以看出,模型预测的排序list中两两pair对相对排序顺序与真实groudtruth中两个pair相对排序顺序一致的pair对越多,则RC计算的分值越大。
6 参考
Learning to Rank wikipedia
Learning to Rank for Information Retrieval
Learning to Rank: From Pairwise Approach to Listwise Approach
earning to rank using gradient descent
Listwise approach to learning to rank: theory and algorithm
Yahoo! Learning to Rank Challenge Overview
Metric Learning to Rank