简单易懂的特征值与特征向量

特征值与特征向量是线性代数中一个很基础的知识，但是很多人对这两个概念没有一个直观的概念，从直觉上，很难理解这两个东西，只知道公式，但是不知道它代表的意义。当年上现代课的时候，老师根本不会去讲这些东西，只是把公式写出来，各种推导，看的人头疼，最后索性也不去理解了，直接背下来，现在想想，体验实在糟糕，我写这篇文章希望能够帮到对这两个概念有疑惑的小伙伴。

当然，为了理解特征值与特征向量，首先要对线性代数有一个基础的了解，我推荐你去看3Blue1Brown的线性代数的本质系列视频：https://www.bilibili.com/video/av6731067。我还偷学了他们的画图技能hhhh。

当然，这个视频里也有关于特征值与特征向量的讲解，不过多个角度和叙述的方式看待问题，对于学习的人来说也是有好处的。如果有时间的话，当然推荐都看看啦～

如何去理解线性代数的概念

说实话，线性代数本身就是一个非常抽象的数学工具，你可以看到它在各个领域中的应用，但学习的时候，大多数的书本里都给的是公式，各种代数上的推导，简单来说，就是让你从数值层面去理解它，虽然对于机器来说，这是小case，但这对于人类无疑是很困难的。

对人类来说，最好是有一个几何的直观的理解，图形对于人来说是非常直观并且可以理解的概念，因此，我更推荐大家在学习线性代数的时候，可以多思考其几何上的意义，矩阵的操作，在2维或3维坐标系中的底发生了什么。不过，超过3维的矩阵，人的脑子中就很难有几何上的直观了，因此，学习的时候仅停留在2，3维即可，当实际应用的时候，有了前面的铺垫，可能自然就有更深刻的理解了。

基底与基向量

基底，是用来描述一个线性空间的基本元素。而组成一个基底的每一个元素，被称为基向量。在一个线性空间中，所有的点（元素）都可以用基底的一组基向量的线性组合来表示。

一般情况下，我们会默认一个基底，这个基底中的每一个基向量的长度相同，并且是正交的（两两相互垂直），在二维坐标系中，就是 $\hat{i} = \binom{1}{0}$ ， $\hat{j} = \binom{0}{1}$ 。
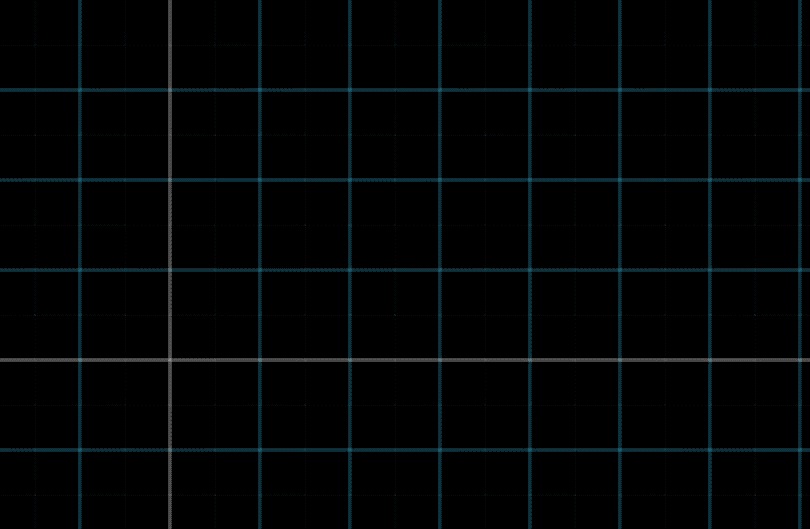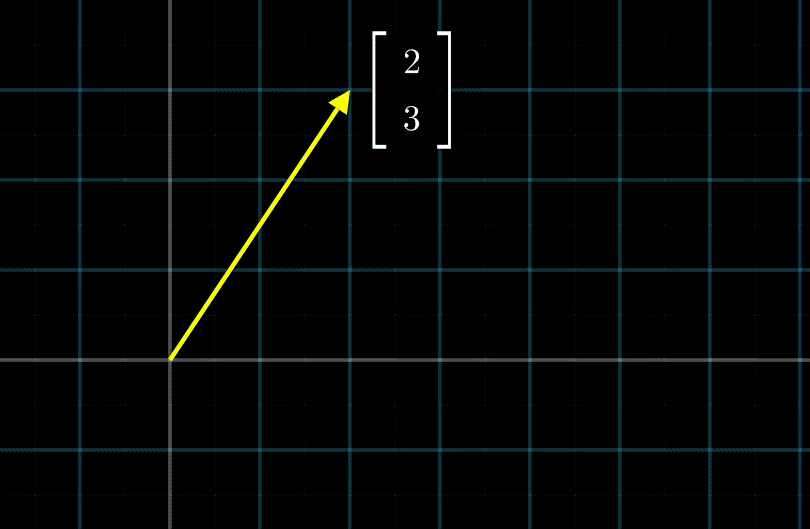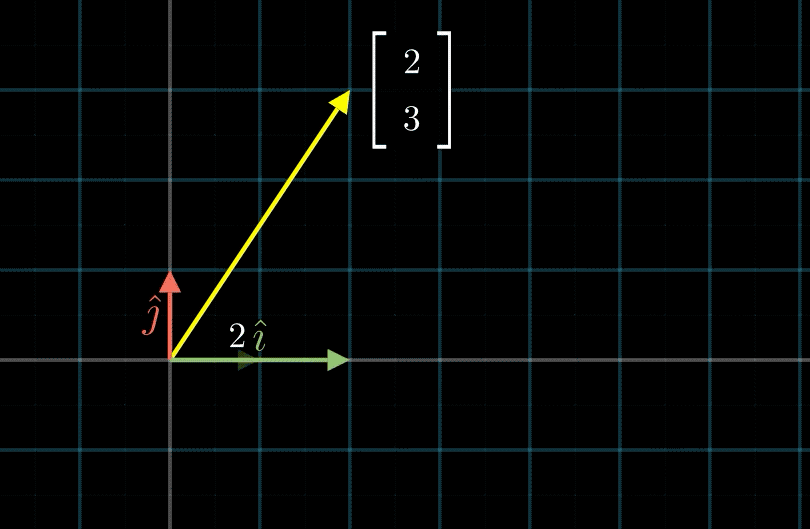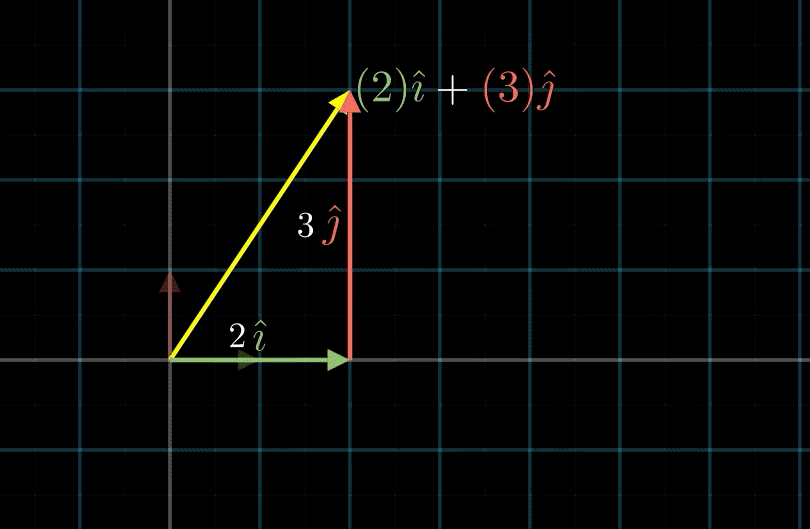
在这里插入图片描述

如上图所示，向量 $\vec{a}=\binom{2}{3} = 2\hat{i} + 3\hat{j}$ 。

上面所说的是很简单很基础的知识，即是不怎么听课也应该知道。但基底的妙处在于，我们可以选择不同的基底来观察整个线性空间，从而达到简化问题的目的。

就和我们经常看到的从不同角度看就不一样的图一样，使用不同的基底来观察线性空间或者某个向量，甚至于某个变换，问题的复杂程度都可能会变得不同。
在这里插入图片描述

如下图所示，还是原来的向量 $\vec{a}=\binom{2}{3}$ ，当我们使用的基底变为 ${\hat{i}}' = \binom{2}{0},{\hat{j}}' = \binom{0}{3}$ 时，向量 $\vec{a}$ 就可以表示为 ${\vec{a}}' = {\hat{i}}' + {\hat{j}}' = \binom{1}{1}$

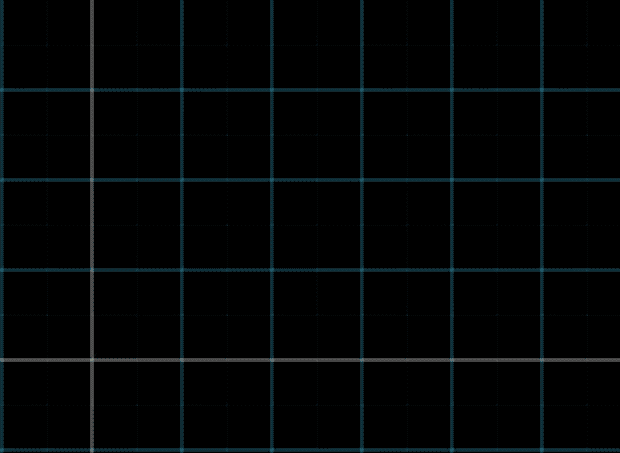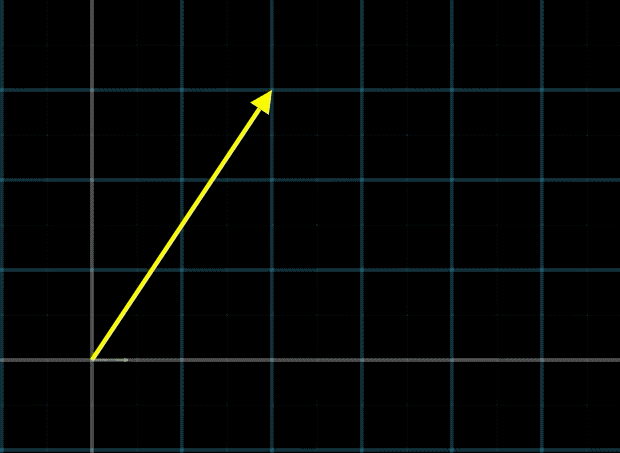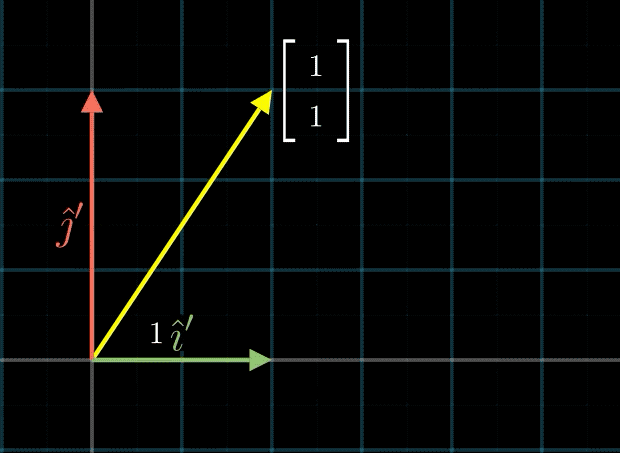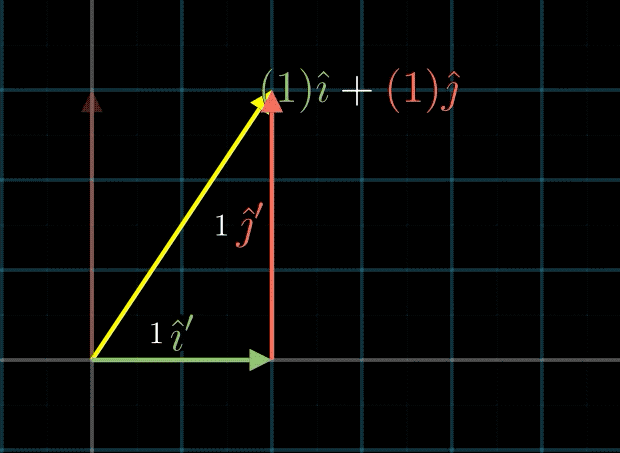
在这里插入图片描述

我们也可以选择不在x轴与y轴，或者非正交的基底，一样可以表示空间内所有的点。当然，这不是随便选的，某些基底的两个向量就无法完成表示空间内所有点的任务，比如共线的两个向量。至于如何判断基底是否可行之类的问题，这里暂时就不讨论了。

在这里插入图片描述

矩阵与线性变换

线性变换，也可以叫做线性映射。通常我们可以通过一个矩阵 $A$ 来表示这个变换（映射），那这个 $A$ 具体是有什么意义的呢？在课堂上，我们通常都学会了计算方法，只知道一个向量 $\vec{x}$ ，乘一个矩阵 $A$ ，得到了向量 $\vec{y}$ ，但是对于变换本身的意义知之甚少。

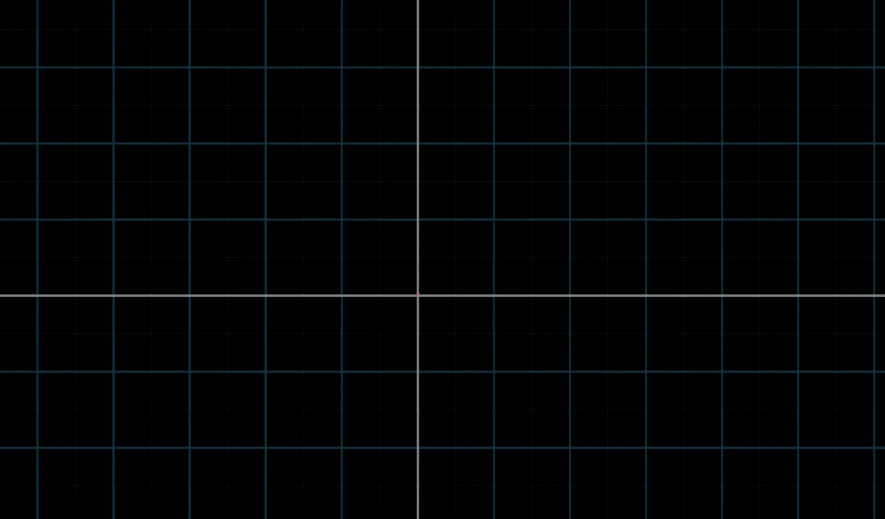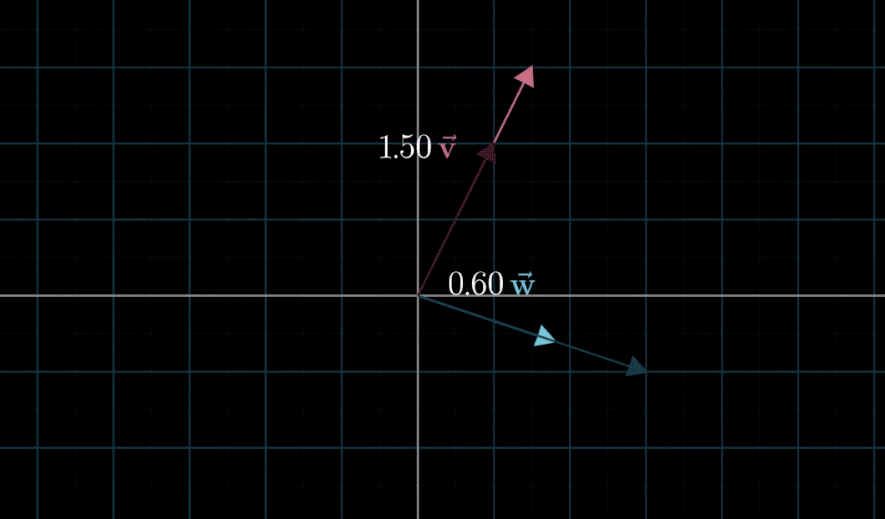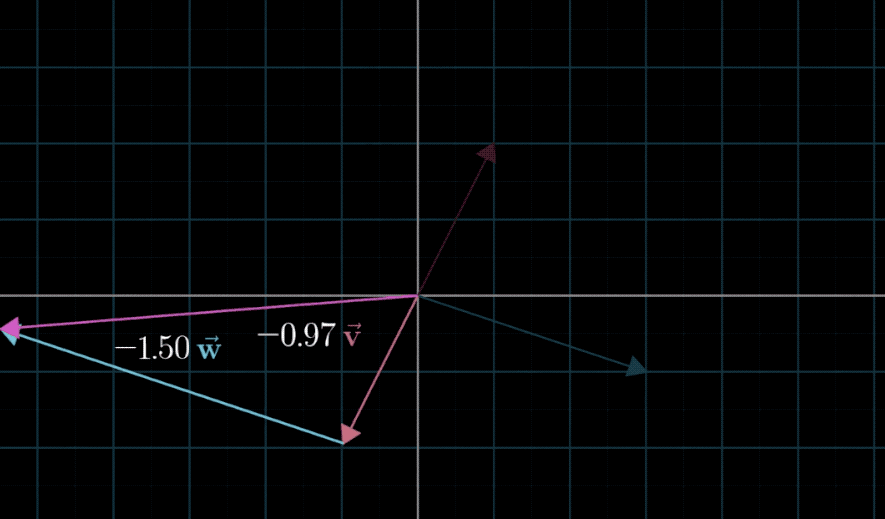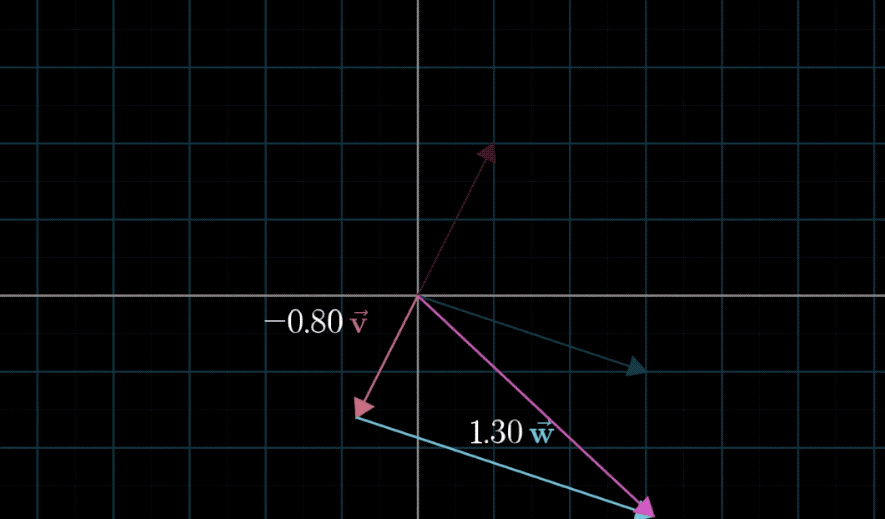
我们来看这个矩阵 $A=\begin{pmatrix} 0 & 2 \\ -1 & -1 \end{pmatrix}$ ，它所对应的变换是什么呢？我们先计算一下一个向量经过变换以后的结果，看看能不能看出来什么，假设 $\vec{x} = \binom{1}{1}$ ，我们可以计算得出 $\vec{y} = A\vec{x} = \binom{2}{-2}$ 嗯，完全没什么感觉。那接下来我把几个向量都经过 $A$ 矩阵变换之后的向量画出来，我们来看看能不能看出什么东西：

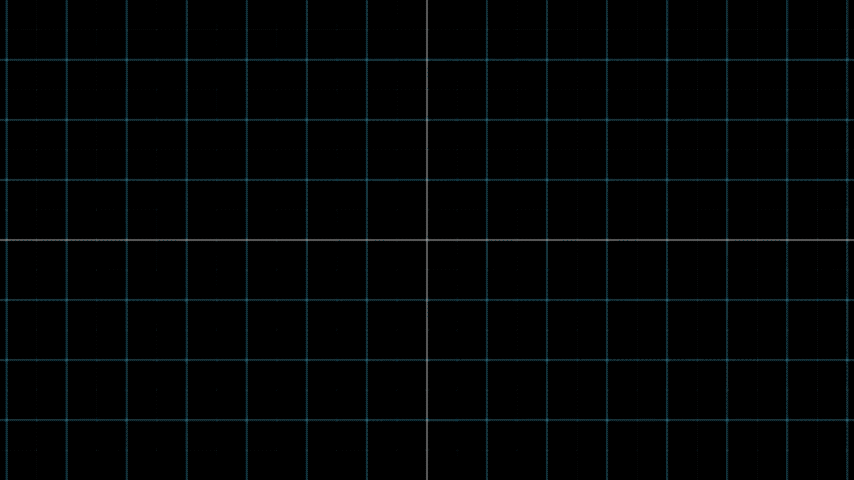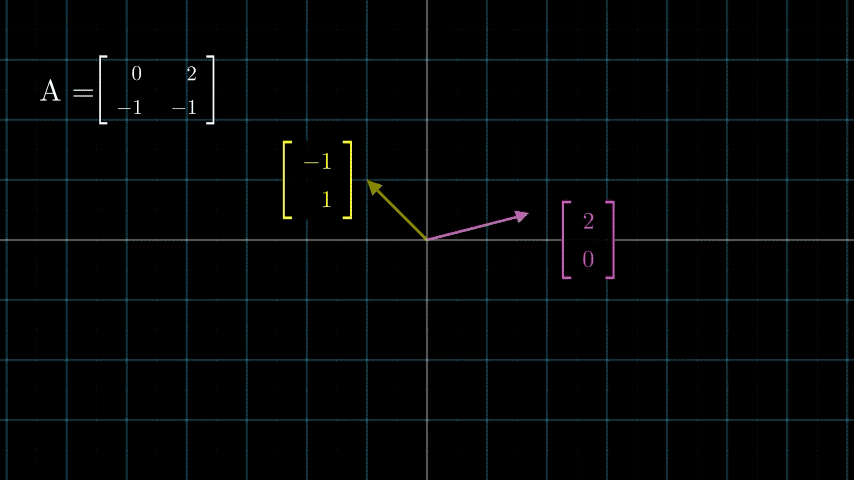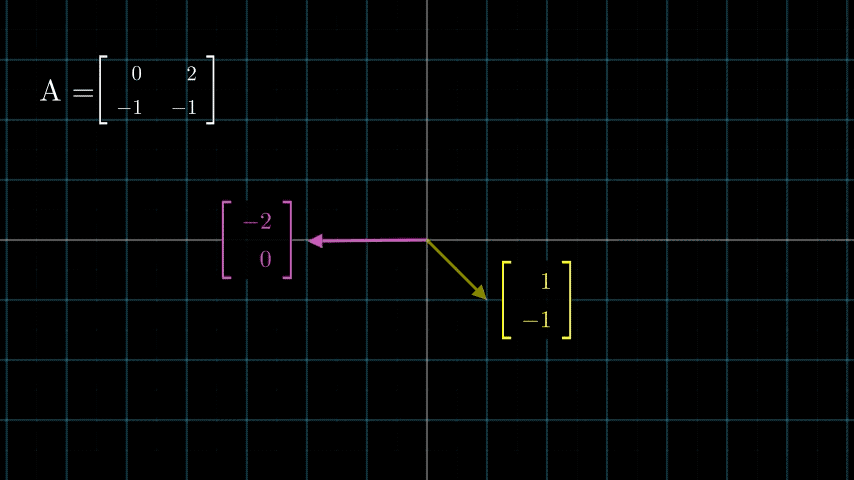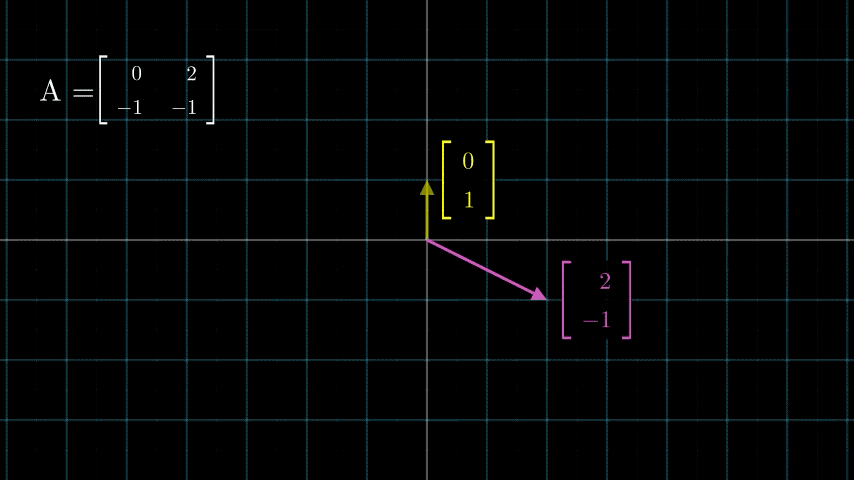
在这里插入图片描述

貌似有一点点规律，向量都是逆时针旋转了一定角度，但是角度却不是全都相同的，有的是90度，有的是145度，而且长度有的发生了变化，有的又没有。说实话，有很长一段时间，我都认为当一个确定的矩阵 $A$ 对不同的向量都做了同样的变换（比如都旋转了90度，都拉伸了2倍这种），然而事实并不是这样。

为了更加直观的看到矩阵 $A$ 所代表的线性变换到底是一个什么样的操作，我们可以将整个坐标系的坐标都进行相同的变换，然后我们就可以看到下面的结果：
在这里插入图片描述

Ok，貌似可以理解这个变换做了什么，那么线性变换有什么性质呢？总结来说，

1.如果一个变换原点保持固定不变， 2. 空间中的直线变换后依然是直线。那么这个变换就可以称作线性变换，而矩阵则是这个变换的数值化表示。接下来又有问题了，怎么把一个线性变换和一个矩阵联系起来呢？

我们还是看矩阵 $A=\begin{pmatrix} 0 & 2 \\ -1 & -1 \end{pmatrix}$ ， $A$ 可以用两个向量表示：

令 $\vec{a_1} = \binom{0}{-1} ，\vec{a_2} = \binom{2}{-1}$

则 $(\vec{a_1} \quad \vec{a_2})$

对于一个向量 $\vec{x} = \binom{x_1}{x_2}$
那么

$A\vec{x}=(\vec{a_1} \quad \vec{a_2})\binom{x_1}{x_2}=x_1\vec{a_1} + x_2\vec{a_2}$

这个形式是不是似曾相识？没错，在上面讲基向量的时候说过，任意一个向量都可以看作是基向量的线性组合。从这个形式来看， $\vec{a_1}$ 和 $\vec{a_2}$ 可以作为一个新的基向量，来表示变换后的所有坐标，也就是说，这个矩阵表示的线性变换的实际意义是基向量变换后的坐标，即基向量 $\vec{i} =\binom{1}{0} \rightarrow \vec{a_1} = \binom{0}{-1}， \vec{j}=\binom{0}{1} \rightarrow \vec{a_2}=\binom{2}{-1}$ 。这也是很多文章或者书中提到的：矩阵就是映射。

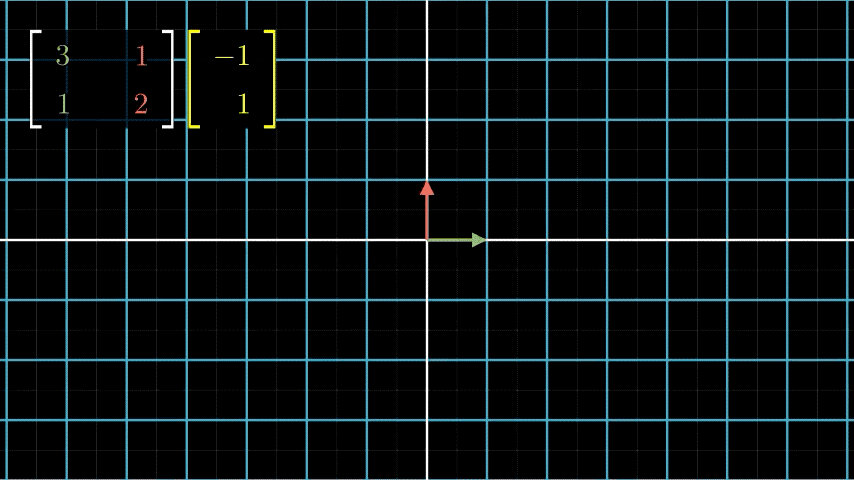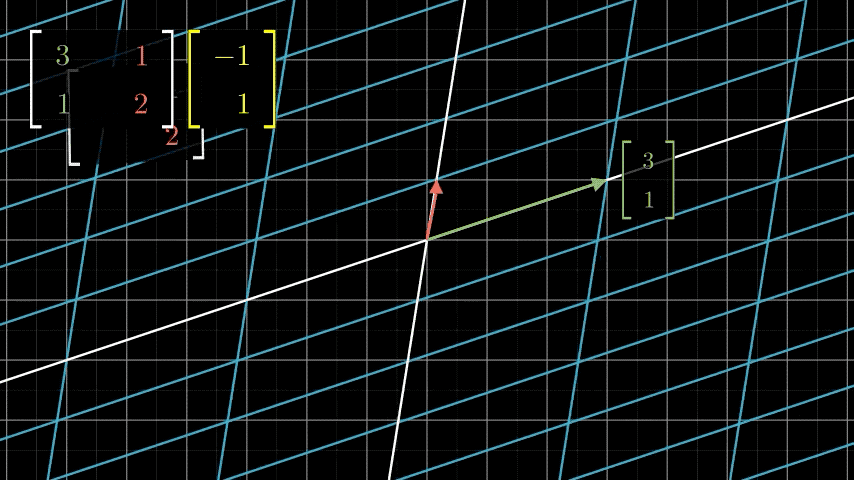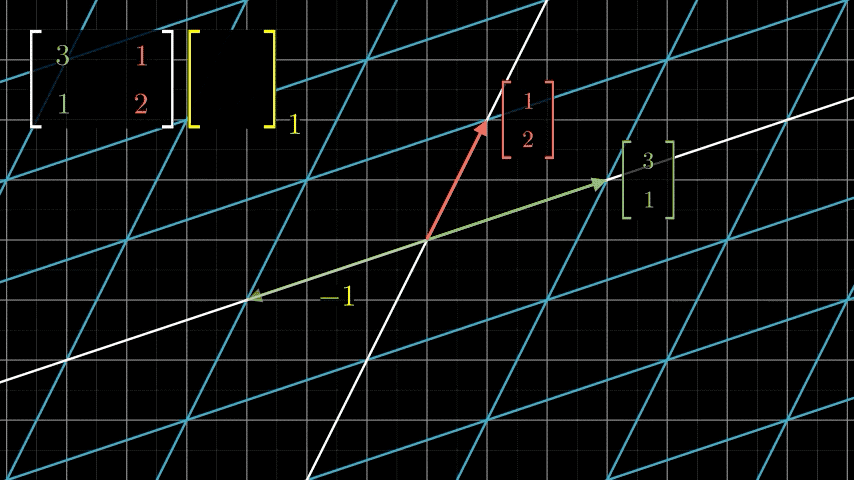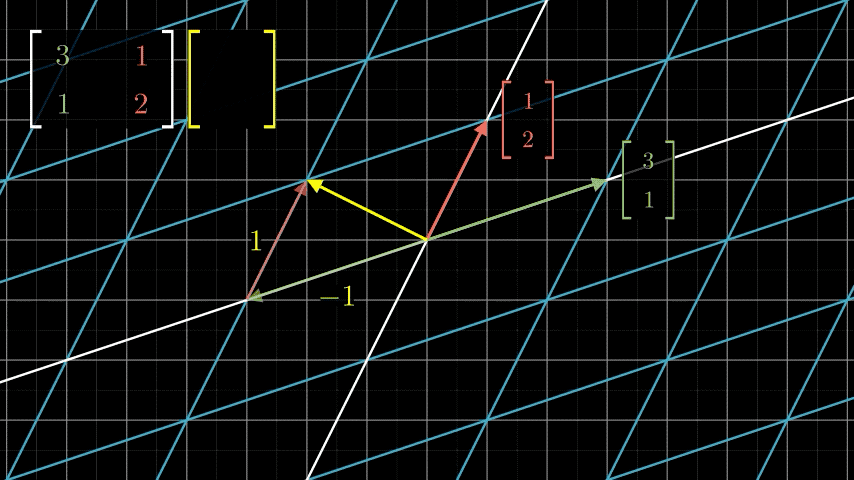
在这里插入图片描述

看上面的动画，经过矩阵变换，新的变量在原来的基表示的线性空间中的坐标表示为 $\binom{-2}{1}$ ，而在新的基向量表示的线性空间的坐标没变，还是 $\binom{-1}{1}$ 。我们既可以把矩阵变换看作是对基的变换，也可以看作是对向量本身的变换，根据情况而定，毕竟我们做这些还是为了简化问题，而不是把问题复杂化。

特征值与特征向量

在讲具体问题之前，我们先来看一下，当我们对线性空间不断做某个线性变换 $A$ ，会发生什么事情：
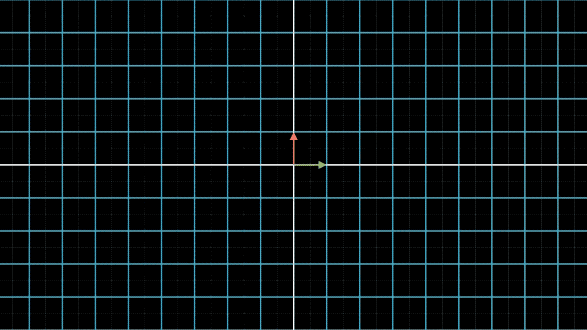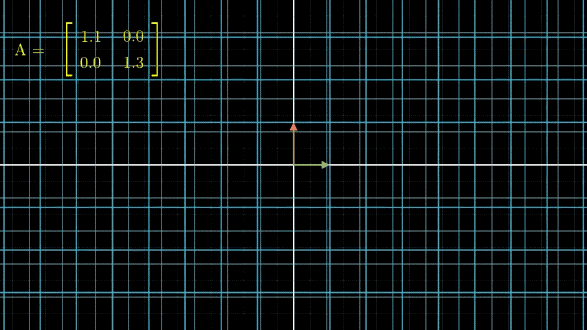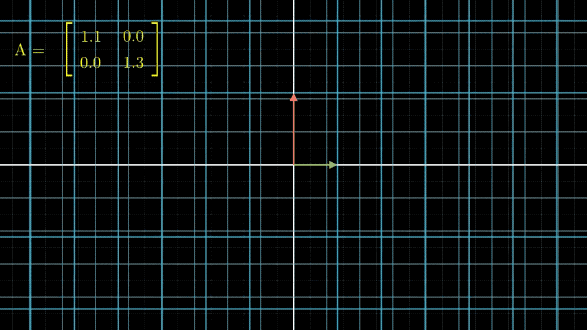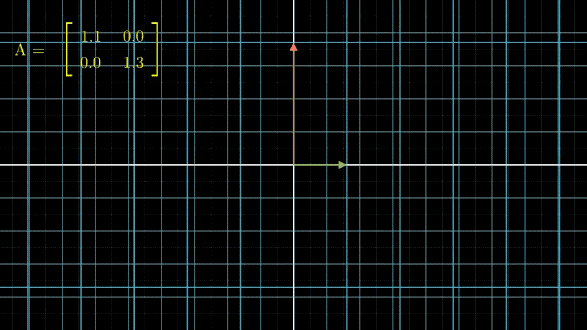
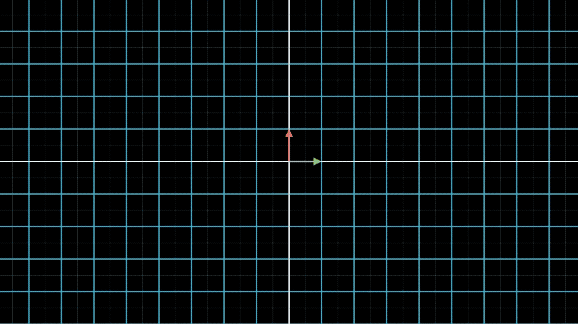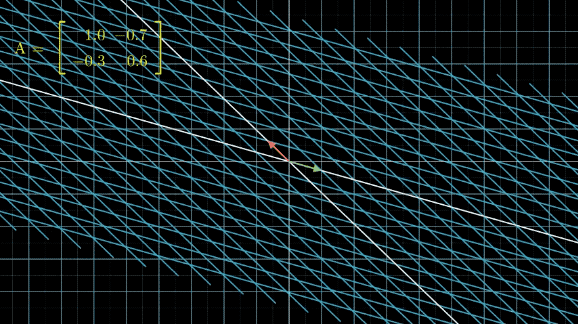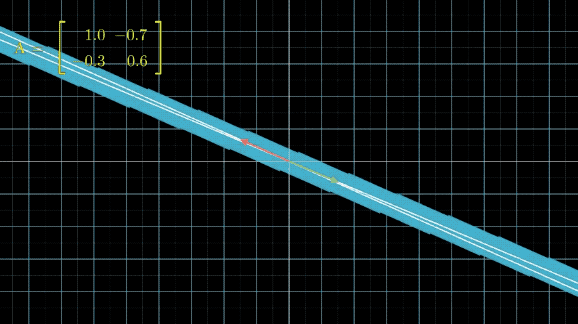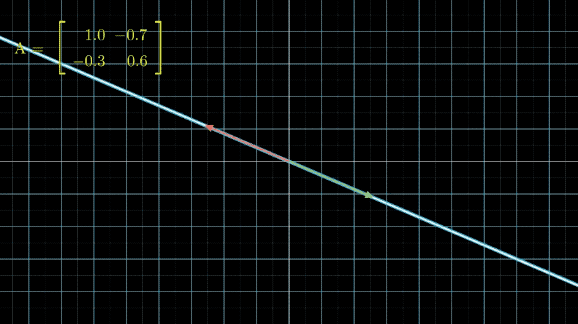
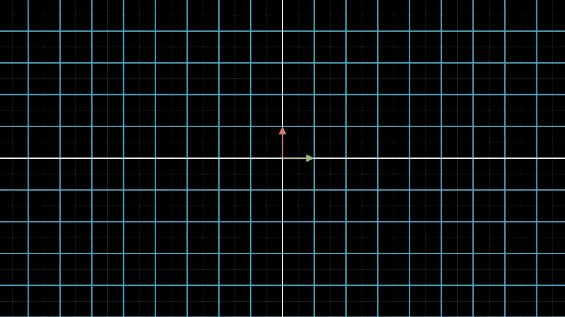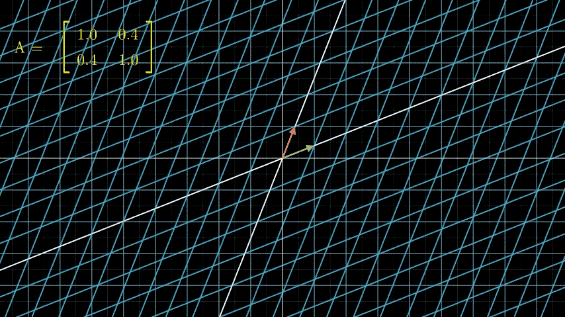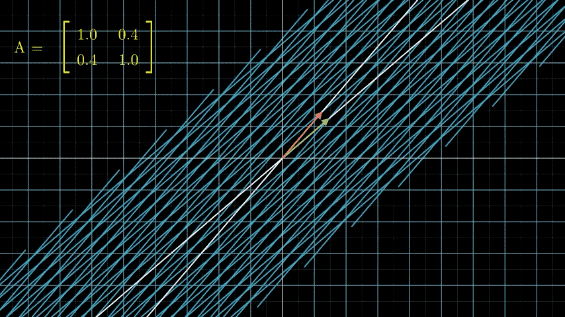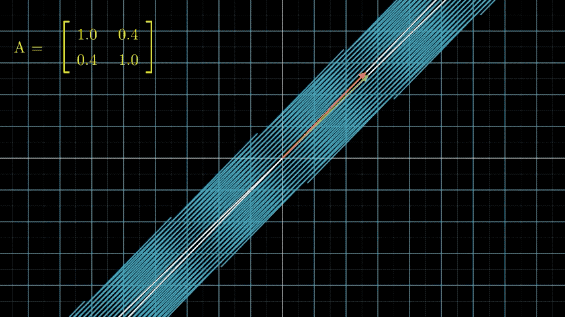
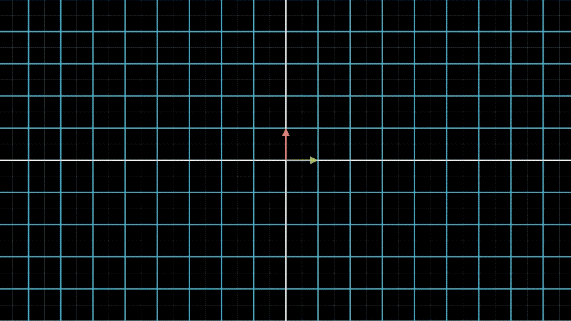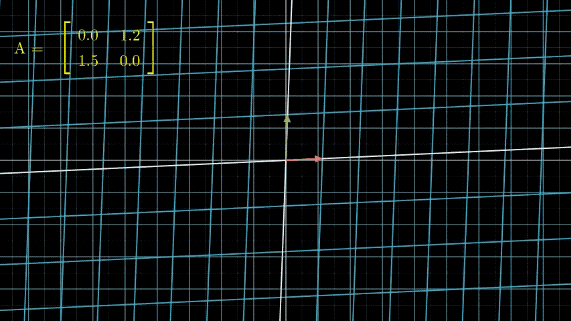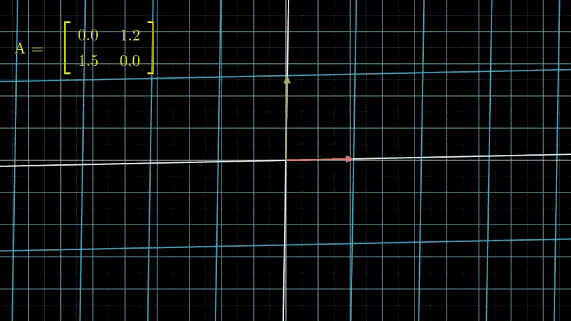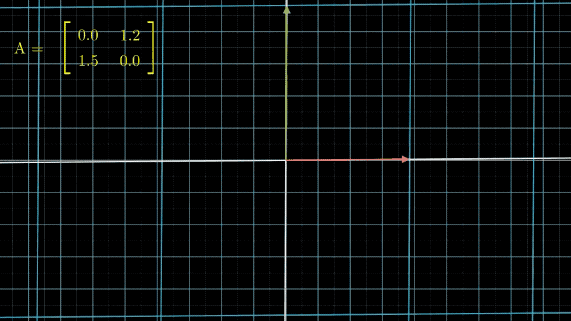
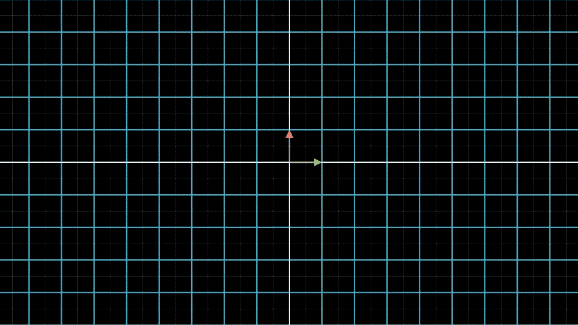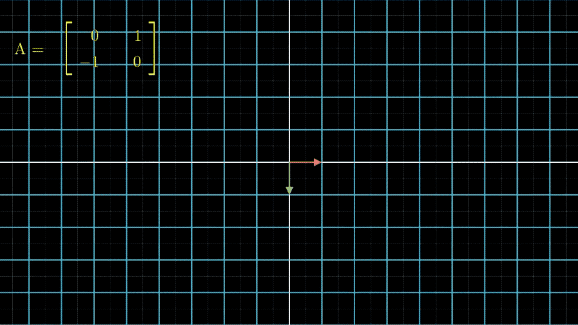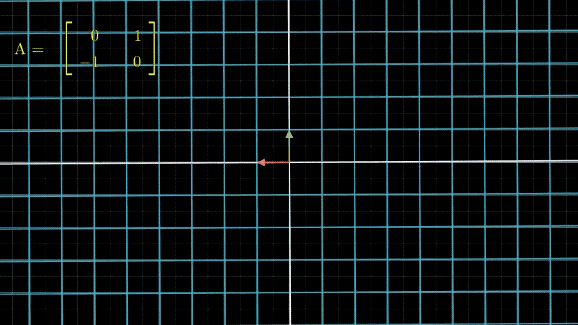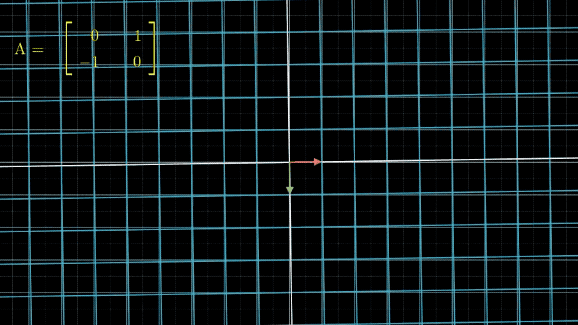
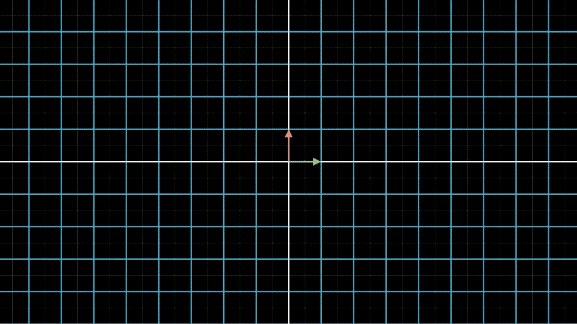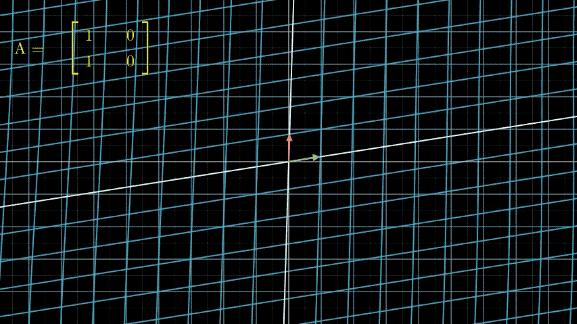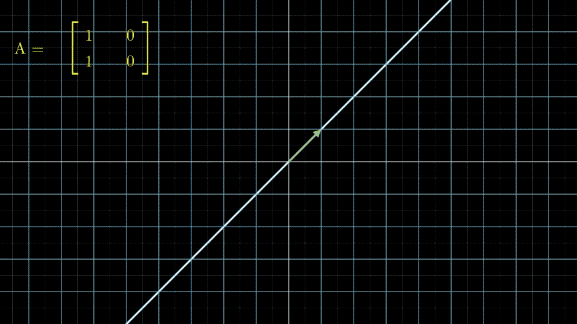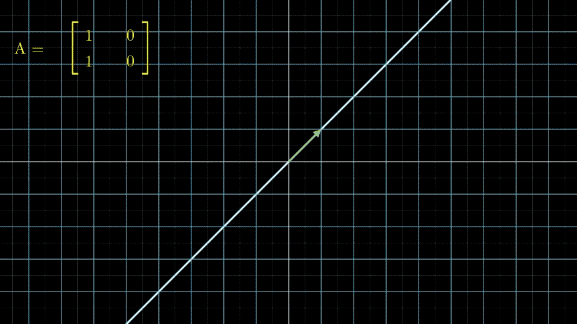
在这里插入图片描述

有没有看晕？其实线性变换基本上是几个基本变换的组合，包括伸缩、旋转、反转、投影（升降维）等。你会发现，这些变换中，第一张图中的变换最简单，这个变换只要给每一维的元素乘上一个系数就行了，不需要和其他维度的元素做组合。还记得前面讲的，选择不同基底，线性空间和线性变换也会发生变化，是不是可以通过这个功能，把所有的变换都谓简单的伸缩呢？用公式来说，就是这样：

设 $t$ 为第t次线性变换

$\vec{x}(t) = A \vec{x}(t - 1) \quad \quad (1)$

这个公式表示每一次进行 $A$ 变换后的向量

$\vec{x}(t) = P\vec{y}(t), \vec{y}(t) = P^{-1}\vec{x}(t) \quad \quad (2)$

上面公式中的 $P^{-1}$ 也是一个变换，这个变换就是上面说的，能够简化问题的变换，为什么不是在基底上做,是因为结果是一样的，也是为了方便做对比和计算。

$\vec{y}(t) = \Lambda \vec{y}(t - 1) \Rightarrow \vec{y}(t) = \Lambda^{t} \vec{y}(0) \quad \quad (3)$

上面的 $\Lambda$ 是一个对角矩阵，也是我们最终要得到的结果。如果我们能找到合适的 $P$ 和 $\Lambda$ ，通过上面的变换，我们就可以简化问题了：通过公式(3)算出 $\vec{y}(t)$ ，再通过公式(2)还原出 $\vec{x}(t)$ 。

接下来把公式推导一下，看看 $P$ 和 $\Lambda$ 要满足的条件：

根据(2)和(3)，可以得到：

$\vec{y}(t) = \Lambda \vec{y}(t - 1) \\ \qquad\qquad = \Lambda P^{-1}\vec{x}(t-1)$

两边同时乘 $P$ 可以得到：

$P\vec{y}(t) = P \Lambda P^{-1}\vec{x}(t-1)$

$\vec{x}(t) = P \Lambda P^{-1}\vec{x}(t-1)$

由此，可以得到：

$\Lambda P^-1 , \Lambda = P^{-1} A P$

因此，最重要的还是要求出这个 $P$ ，它要满足两个性质，一个是 $P$ 必须是个可逆矩阵，另一个是 $P^{-1} A P$ 要是一个对角矩阵。

推了一堆公式，希望你的脑子还没乱。接下来我们看一下，求出这个 $P$ 以后，将 $\vec{x}$ 转化为 $\vec{y}$ 再应用变换 $\Lambda$ ，与直接使用变换 $A$ 有什么区别。

我随便写了个矩阵：

$A=\begin{pmatrix} 1 & 0.1 \\ 0.2 & 0.8 \end{pmatrix}$

求出了 $P,P^{-1},\Lambda$ (保留3位小数):

$P=\begin{pmatrix} 0.977 & 0.358 \\ -0.614 & 0.840 \end{pmatrix},P^{-1}=\begin{pmatrix} 0.807 & -0.344 \\ 0.591 & 0.939 \end{pmatrix},\Lambda=\begin{pmatrix} 1.073 & 0 \\ 0 & 0.727 \end{pmatrix}$

第一个图，就是不断的应用线性变换 $A$ ：
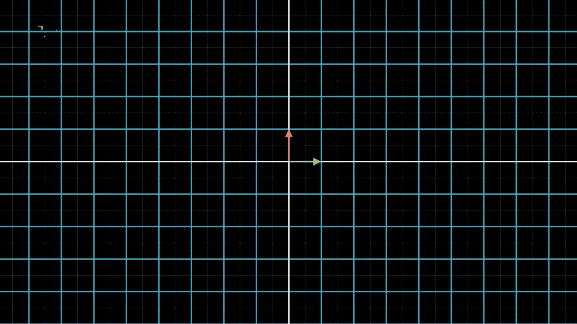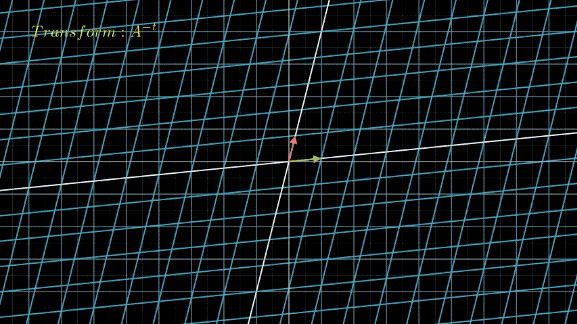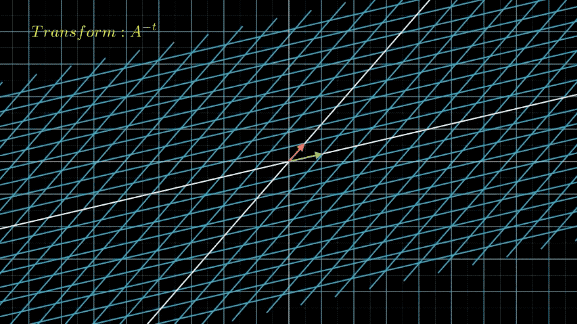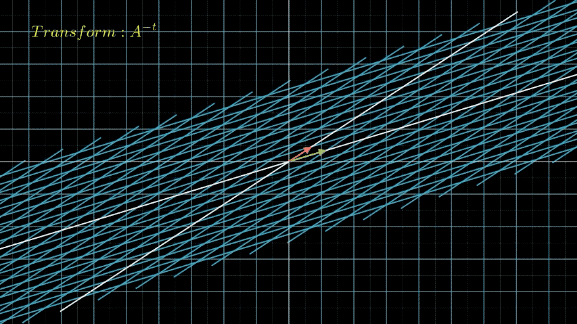
在这里插入图片描述

接下来，我们将线性空间先应用变换 $P^{-1}$ ，把空间中的 $\vec{x}$ 都转化为对应的 $\vec{y}$ ，然后不断应用变换 $\Lambda$ ：

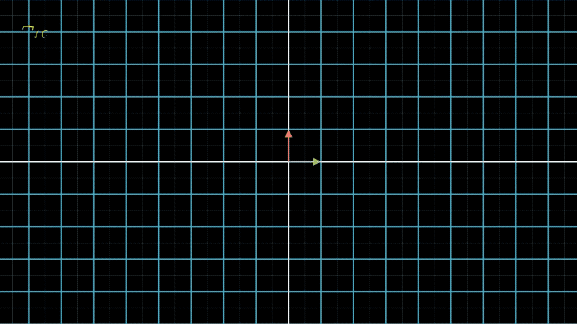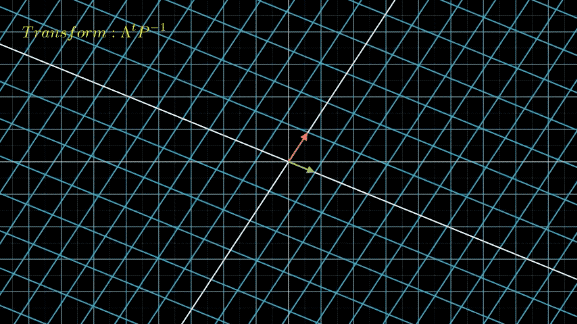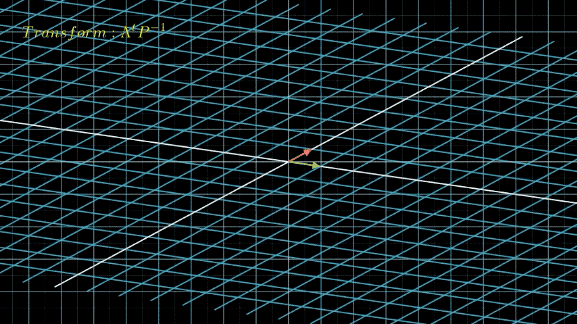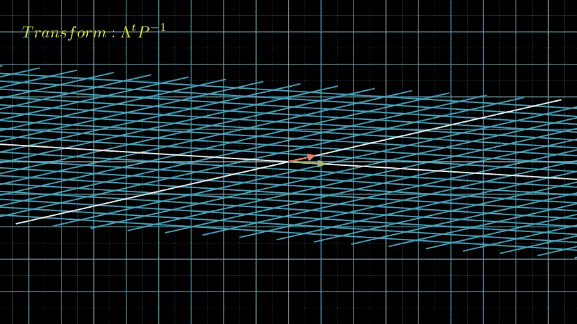
在这里插入图片描述

从肉眼中看，这两个变换区别不大，只是下面的转了个角度而已，而且从公式上看，下面的变换再左乘个 $P$ ，就和上面的完全一样了。

这么看的话就大概明白这个操作是什么干什么的了，就像是我们要从中山公园坐地铁到南京东路，明明2号线（绿色）是最近的，换乘少的，你偏要转4号线（深紫色），再转10号线（浅紫色），然后到南京东路。为啥要这么做呢，有可能是10号线人少，能抢到座，也有可能是为了接个人之类的。

在这里插入图片描述

那么回归到我们做这些操作，同样也是为了谋求某些便利，或者为了简化问题，具体有啥用，再后面会简单说一说。现在，先把这一节的主题说一下，上面讲的这一堆，和特征值与特征向量究竟有毛的关系？

下面又要推公式了，不过不要慌，前面已经做好了铺垫，接下来只需要把公式变一下形式就可以了。

首先，我们把 $P$ 分解为 $n$ 个 $n$ 维的列向量：

$P=(p_1, ..., p_n)$

我们想要找到一个能够满足对角矩阵 $\Lambda$ 的 $P$ ：

$P^{-1} A P = \Lambda = diag(\lambda_1,...,\lambda_n)$

上式中 $d i a g ()$ 表示对角矩阵， $\lambda_i$ 表示对角矩阵中对角线上元素的值。

对上式做变形，两边同时左乘 $P$ ：

$P^{-1} A P = \Lambda \Rightarrow AP=P\Lambda$

即：

$A(p_1,...,p_n) = (p_1, ...,p_n)\begin{pmatrix} \lambda_1 & 0 & 0 \\ 0 & ... & 0 \\ 0 & 0 & \lambda_n \end{pmatrix}$

利用分块矩阵，分别计算两边：

$(Ap_1,...,Ap_n) = (\lambda_1 p_1, ..., \lambda_n p_n)$

两边的每个元素都单独拿出来，可以发现：

$Ap_1 = \lambda_1p_1$

$Ap_i = \lambda_ip_i$

$Ap_n = \lambda_np_n$

看到这里，学习过线性代数的同学是不是仿佛看到了令人很亲切的公式呢？

$\lambda p \quad\quad (p \neq o)$

满足上面公式的数值 $\lambda$ 称之为特征值，向量 $p$ 称之为特征向量。

从上面的一些公式上就可以看出一些特征值与特征向量性质：

对特征向量进行 $A$ 矩阵所代表的线性变换，特征向量的方向是不变的。
特征向量 $p$ 的倍数 $\alpha p$ 也是一个特征向量，对应的特征值是 $\alpha \lambda$ 。也就是说，一组特征向量和特征值的表示方式并不是唯一的。当然，通常使用的时候，我们会把向量归一化到单位向量。
特征向量的顺序不同会导致构造的 $P$ 矩阵也不一样，得到的对角矩阵 $\Lambda$ 也不同，当然，特征值还是要一一对应的。
通过特征值与特征向量，可以"还原"一个线性变换 $A$ （ $\Lambda P^-1$ ），也就是说，可以用特征值与特征向量表示一个线性变换。

暂时就列几条想到的，更多的性质可以自己思考或者找一些别的资料，我担心我也列不全。另外，并不是所有的矩阵都存在实数范围内的特征值和特征向量，比如旋转的线性变换，因为不存在一个在这个变换后，方向还不变的向量，但是具体如何判断，这里就暂且不讲了。总结来说，特征值与特征向量并不是那么难以理解，可以看作是线性变换的另一种表示方法，也可以看作是改变了基底的线性变换，只要能够理解我们是怎么通过通过这一顿操作，得到的这些有用的公式，它们有哪些好用的性质就行了。接下来我就简单讲一下特征值和特征向量究竟有什么用。

特征值与特征向量的应用

有很多算法中会使用到特征值与特征向量，比如主成分分析，图片压缩，某些分类问题……这里我不打算把这些应用一一解释，因为会太长了，有空可以单独拿出一个问题详细说一下，比如主成分分析之类的。这一节主要是简单讲一下这些算法大概是如何利用了特征值与特征向量的性质的。

基本上，这些算法主要都利用了特征值与特征向量的两个性质，我上一节也提到了，一个是特征值与特征向量可以表示一个线性变换，另一个是特征向量在构造矩阵 $P$ 的时候顺序可以变化。

首先我们可以看一下一个有点特殊的对角矩阵对一个向量做线性变换的情况：
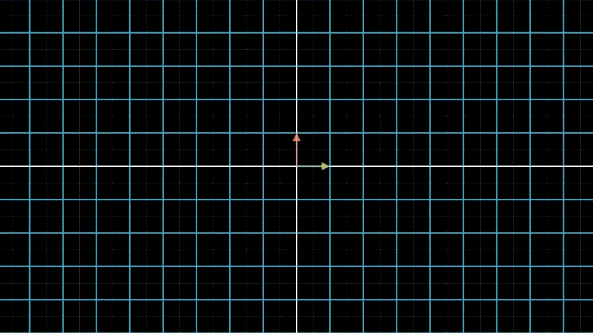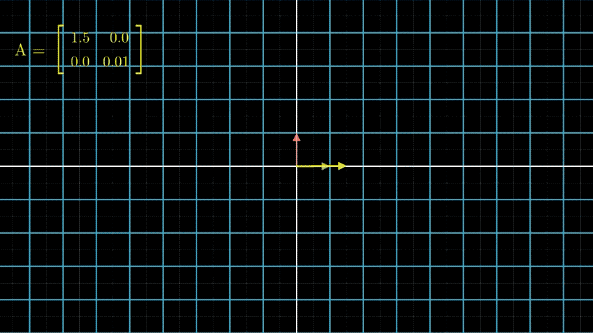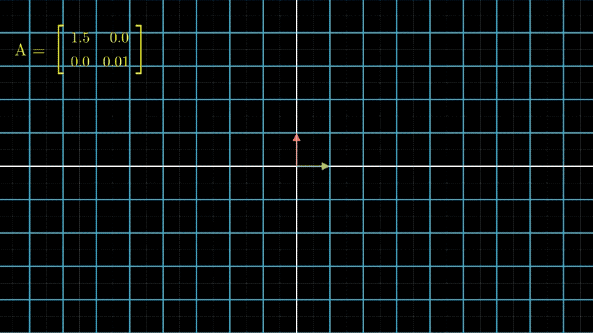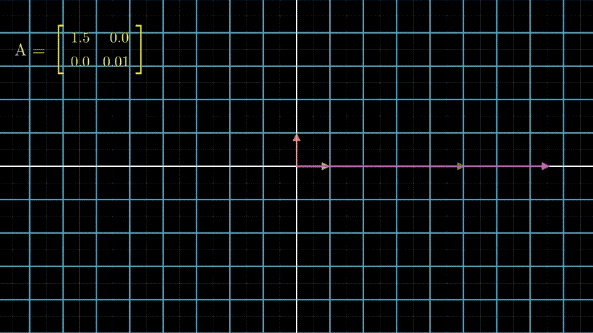
在这里插入图片描述

可以发现，当对角矩阵的某个值相对来说特别小的时候，那么在这个方向上的变化基本不会影响最终的结果。这是二维的情况，三维可以自行想象一下，更多维的结论也是相同的。

回过头来，我们可以想一下我们得到的特征值，如果我们把特征值按照大小排列，并定一个阈值，把小于这个值的特征值与对应特征向量忽略（相当于置0），那么我们就能得到一组新的特征值与特征向量，并且这组特征值与特征向量所表示的线性变换与我们原来的线性变换几乎是相同的，这就达到了降维或压缩数据的目的。另外，特征值的大小也反应了这个方向在整个变换的重要程度，而对应的特征值是原始矩阵的一组线性组合，利用这个，也可以分析原始矩阵中哪些元素是决定性的，这个在做分类或者寻找某些特征的时候会比较好用。