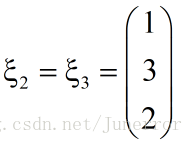1. 特征值和特征向量

在讨论特征值和特征向量之前，必须声明的是现在我们关注的是有限维 线性空间上的线性变换。这里两个关键词：一个是有限维，一个是线性空间。关于这两个专业名词的定义，可以参见下面的博文。

1.1 特征值和特征向量的通俗解释

首先，推荐b站上的视频讲解. 想看文字版的可以继续往下看。

向量x左乘一个方阵A，得到的还是一个向量。但是此时向量的方向还有大小可能都发生了改变，所以向量左乘一个矩阵可以看成是对向量的拉伸和旋转。

特征值和特征向量的定义就是$Ax=\lambda x$，其中，$x$是非零向量。

看这个公式的左边是一个方阵乘以一个向量，得到的还是一个向量这是毋庸置疑的，但是公式的右边还是关于x的一个向量，仅仅是做了一个伸缩变换而已。所以特征值和特征向量，可以这样去理解：
如果存在的话，对于方阵A，我们能找到这样的向量x,使得经过A的伸缩和旋转以后，还是在x所指的正方向或者反方向的线上。关于向量的大小可以通过$\lambda$来调节。

1.2 如何计算矩阵的特征值和特征向量

对于$Ax=\lambda x$，我们可以先做如下的变形，也就是$(A-\lambda I)x=0$, 这也就变成了线性方程组求解的问题，我们知道对于线性方程组而言，如果x存在非0解的话，也就是$|\lambda I-A|=0$。于是我们可以确定$\lambda$的取值，进而确定特征向量的取值。

关于练习题的话，大家可以在网上搜索一下，比如下面这个例子.
特别注意的是，特征向量并不是唯一的，尤其是在做初等变换的时候有不同的变换方式。

1.3 特征多项式

我们在计算特征值和特征向量的时候，我们用到$|\lambda I-A|=0$，其中$|\lambda I-A|$就叫做特征多项式。

1.4 特征值和特征向量的性质

1. 相似矩阵有相同的特征多项式，相同的特征值。
   
2. A是可逆矩阵，A的特征值是${\lambda }_1,{\lambda }_2,\dots$,那么其逆矩阵的特征值是${\lambda }_1^{-1},{\lambda }_2^{-1},\dots$，这个的证明也很简单
   
3. 假设A的特征值是${\lambda }_1,{\lambda }_2,\dots$,$f(x)$是一个多项式，那么$f({\lambda }_1),f({\lambda }_2),\dots$是$f(A)$的全部特征值，这个的证明也很简单