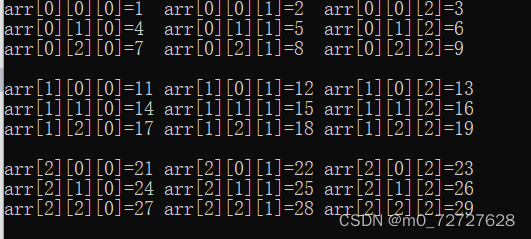
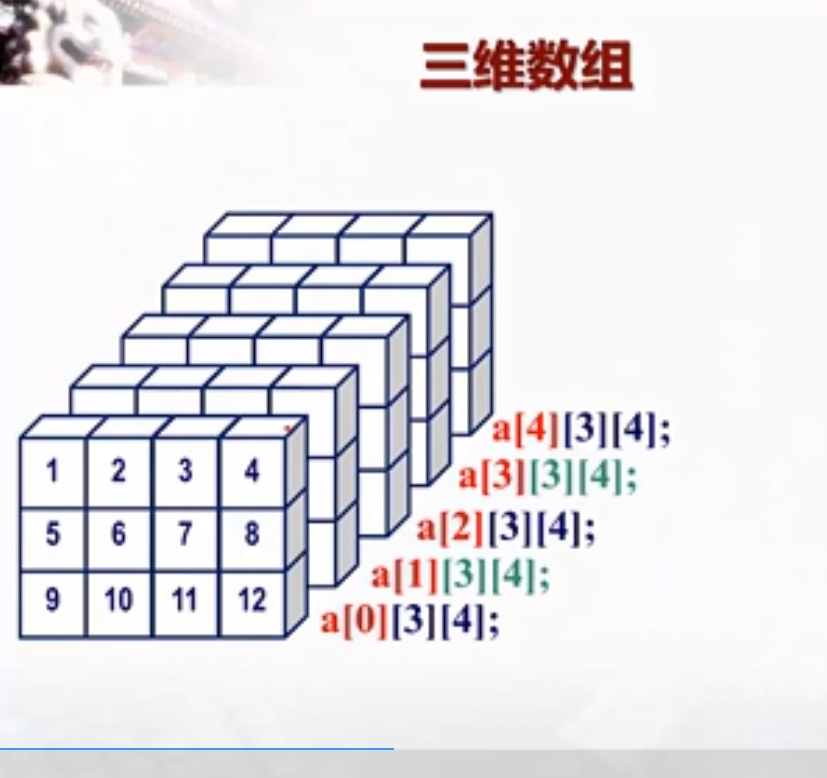
二维数组或三维数组转为一维数组
1.二维数组转换为一维数组:
设二维数组a[i][j],数组a行数x行,列数y列;
一维数组b[n],数组b最多存储m=x*y个元素。
令x=3,y=4则:m=12
此时,数组a中元素的位置序号(i j)为:
00 01 02 03
10 11 12 13
20 21 22 23
数组b中元素的位置序号(n)为:
0 1 2 3
4 5 6 7
8 9 10 11
数组a中每一行位置j的序号均为:0 1 2 3
因此,数组b中元素的位置序号可写成:
0+0 1+0 2+0 3+0
4+0 4+1 4+2 4+3
8+0 8+1 8+2 8+3
数组a中每列位置i的序号均为:0 1 2
因此,数组b中元素的位置序号可写成:
0*4+0 0*4+1 0*4+2 0*4+3
1*4+0 1*4+1 1*4+2 1*4+3
2*4+0 2*4+1 2*4+2 2*4+3
由上述数组b中元素的位置序号可得:
n=i*y+j,其中y为数组a的列数,此例中y=4。
综上所述,经猜想与反复验证数组a中元素的位置序号(i j)与
数组b中元素的位置序号(n)的关系为;n=i*y+j(y为数组a的列数)
代码如下:
#include<stdio.h>
#define x 3//宏定义数组每列存储元素的最多个数
#define y 4//宏定义数组每行存储元素的最多个数
void main()
{int a[x][y],b[100],i,j,n,m;printf("enter %d elements:\n",x*y);for(i=0;i<x;i++){for(j=0;j<y;j++){scanf("%d",&a[i][j]);//输入二维数组存储元素}}printf("The 2D array is:\n");for(i=0;i<x;i++){for(j=0;j<y;j++){printf("a[%d][%d]=%d ",i,j,a[i][j]);//输出二维数组存储元素}printf("\n");//以每行y个元素的格式输出}for(i=0;i<x;i++){for(j=0;j<y;j++){b[j+i*y]=a[i][j];//二维数组转一维数组}}printf("The 1D array is:\n");for(n=0,m=1;n<x*y;n++,m++){printf("b[%d]=%d ",n,b[n]);//输出一维数组存储元素if(m%3==0){printf("\n");//以每行3个元素的格式输出}}
}
运行结果如下:
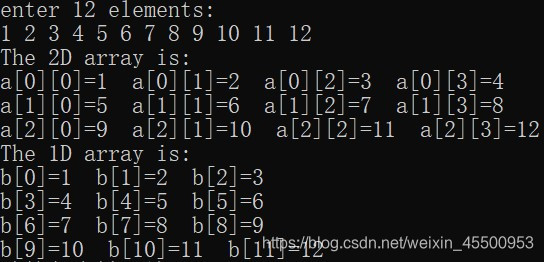
2.三维数组转换为一维数组:
设三维数组a[i][j][k],数组a中x轴方向最多有x个元素,
y轴方向最多有y个元素,z轴方向最多有z个元素。
一维数组b[n],数组b最多存储m=x*y*z个元素。
令x=3,y=2,z=2则:m=12
此时,数组a中元素的位置序号(i j k)为:
000 001 002
010 011 012
100 101 102
110 111 112
数组b中元素的位置序号(n)为:
0 1 2
3 4 5
6 7 8
9 10 11
因猜想过程难以描述,所以此处省略猜想过程。
数组b中元素的位置序号(n)最终可写成:
3*(2*0+0)+0 3*(2*0+0)+1 3*(2*0+0)+2
3*(2*0+1)+0 3*(2*0+1)+1 3*(2*0+1)+2
3*(2*1+0)+0 3*(2*1+0)+1 3*(2*1+0)+2
3*(2*1+1)+0 3*(2*1+1)+1 3*(2*1+1)+2
由上述数组b中元素的位置序号可得:
n=x(y*i+j)+k,其中x为数组a在x轴方向存储元素的最多个数,
y为数组a在y轴方向存储元素的最多个数,此例中x=3,y=2。
综上所述,经猜想与反复验证数组a中元素的位置序号(i j k)与
数组b中元素的位置序号(n)的关系为;
n=x(y*i+j)+k(x为数组a在x轴方向存储元素的最多个数,
y为数组a在y轴方向存储元素的最多个数)
代码如下:
#include<stdio.h>
#define z 2//宏定义数组在z轴方向存储元素的最多个数
#define y 2//宏定义数组在y轴方向存储元素的最多个数
#define x 3//宏定义数组在x轴方向存储元素的最多个数
void main()
{int a[z][y][x],b[100],i,j,k,m,n;printf("enter %d elements:\n",z*y*x);for(i=0;i<z;i++){for(j=0;j<y;j++){for(k=0;k<x;k++){scanf("%d",&a[i][j][k]);//输入三维数组存储元素}}}printf("The 3D array is:\n");for(i=0;i<z;i++){for(j=0;j<y;j++){for(k=0;k<x;k++){printf("a[%d][%d][%d]=%d ",i,j,k,a[i][j][k]);//输出三维数组存储元素}printf("\n");//以每行x个元素的格式输出}}for(i=0;i<z;i++){for(j=0;j<y;j++){for(k=0;k<x;k++){b[x*y*i+x*j+k]=a[i][j][k];//三维数组转一维数组}}}printf("The 1D array is:\n");for(n=0,m=1;n<x*y*z;n++,m++){printf("b[%d]=%d ",n,b[n]);//输出一维数组存储元素if(m%3==0){printf("\n");//以每行3个元素的格式输出}}
}
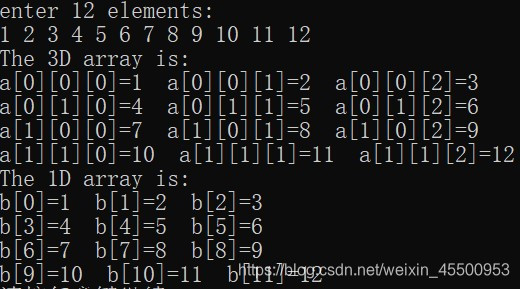
运行结果如下: