求特征根

特征方程的求解
在这里插入图片描述

A=[1 7 16 12]
r=roots(A)

结果
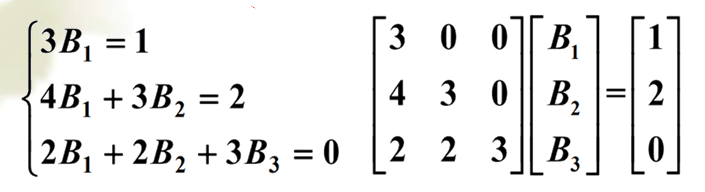
在这里插入图片描述

求线代数方程组

在这里插入图片描述

format rat
A=[3 0 0; 4 3 0;2 2 3]; %左边
C=[1 2 0]'; %右边
B=inv(A)*C

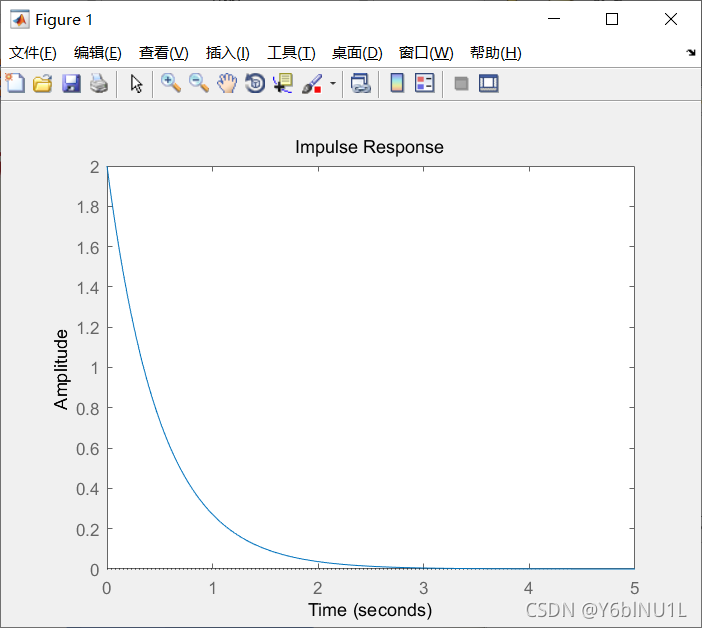
在这里插入图片描述

求单位冲激响应

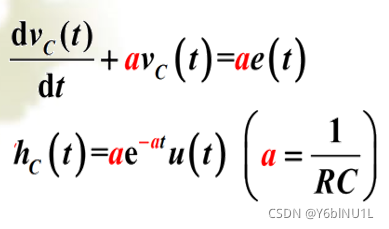
在这里插入图片描述

a=2;
t=0:0.01:5;
A=[1 a];
B=[0 a];
impulse(B,A,t)

在这里插入图片描述

零状态冲激响应

在这里插入图片描述

syms t;
y1=exp(-2*t)*cos(3*t)*heaviside(t);%原表达式，其中heaviside函数是单位阶跃函数，matlab自带的函数
y2=diff(y1)  %diff是求导函数
y3=simplify(y2)  %所得是零状态响应表达式

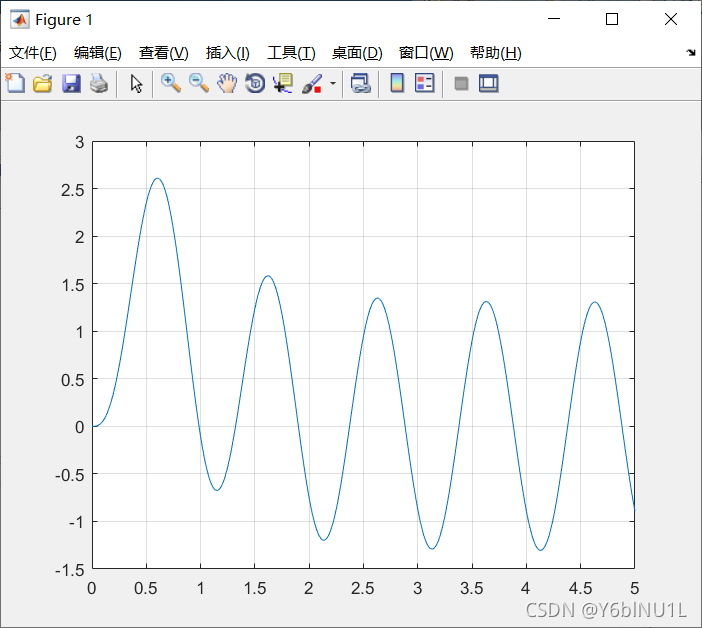
在这里插入图片描述

零状态响应的数值求解

在这里插入图片描述

t=0:0.01:5;
sys=tf([6],[1 5 6]) %右边，左边
f=10*sin(2*pi*t).*heaviside(t) %heaviside是单位阶跃函数，自带
y=lsim(sys,f,t)
plot(t,y)
grid

在这里插入图片描述

冲激响应和阶跃响应的数值求解

冲激响应和阶跃响应

在这里插入图片描述

t=0:0.01:5;
sys=tf([1 16],[1 2 32]) %右边,左边
h=impulse(sys,t) %计算冲激响应
g=step(sys,t) %计算阶跃响应
subplot(2,1,1)
plot(t,h)
grid;
subplot(2,1,2)
plot(t,g)
grid;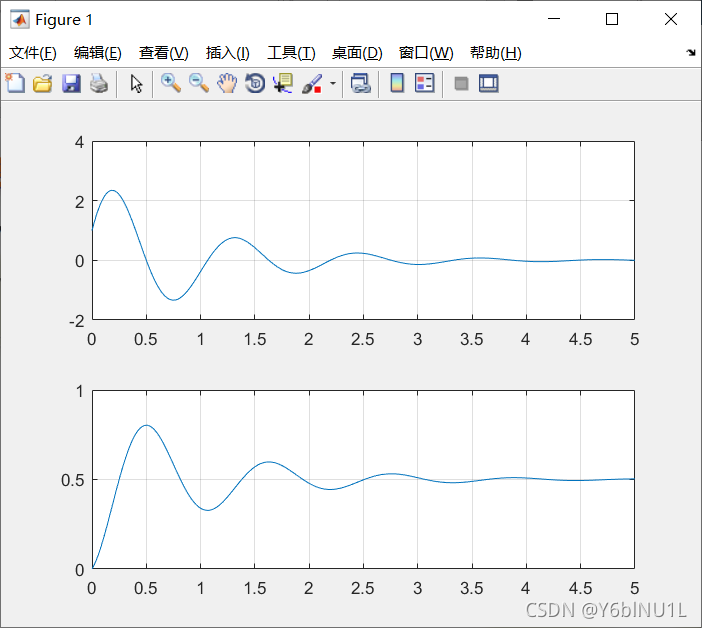

在这里插入图片描述

零状态与零输入响应的求解

零状态响应求解

使用lsim函数用来求解零初始条件的微分方程
y=lsim(sys,f,t);其中t表示系统响应的抽样点向量，f是系统输入信号向量，sys是LTI系统模型，用来表示微分方程，差分方程和状态方程。

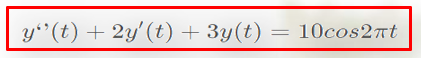
在这里插入图片描述

b=[1] %微分方程的右端
a=[1 2 3] %微分方程的左端
ts=0;te=5;dt=0.01;
sys=tf(b,a);
t=ts:dt:te;
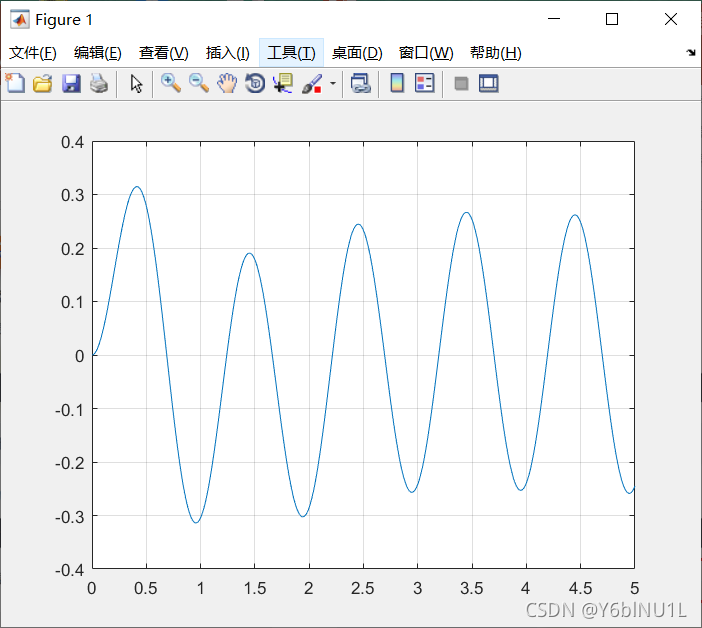
f=10*cos(2*pi*t);
y=lsim(sys,f,t);
plot(t,y);
grid on;

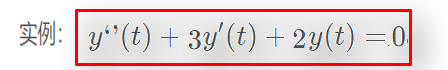
在这里插入图片描述

零输入响应求解

在这里插入图片描述

ts=0;te=5;dt=0.01;
t=ts:dt:te;
%eq表示各微分方程，用Dy，D2y，D3y表示y的一阶导，二阶导，三阶导
eq='D2y+3*Dy+2*y=0'; %齐次解求零输入响应
%cond表示初始条件或者其实条件
cond='y(0)=1,Dy(0)=2';
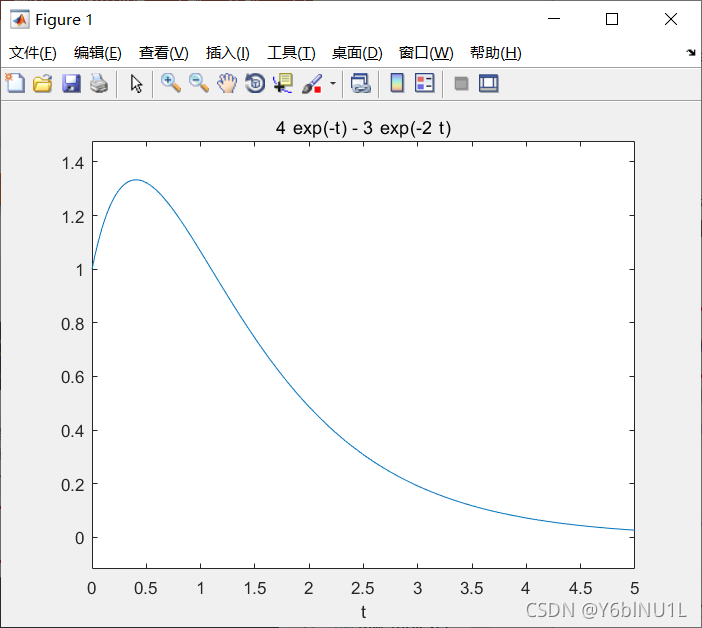
yzi=dsolve(eq,cond,'t') %第三个参数表示自变量，默认自变量是t
ezplot(yzi,t) %绘制符号函数的图像，只需给出函数的解析表达式即可，不需计算，也可不指出绘图区间，是一种十分简单的绘图方式。

在这里插入图片描述